更多有关排序的话题

跟Python内置的列表一样，ndarray的sort实例方法也是就地排序。也就是说，数组内容的重新排列是不会产生新数组的：

  1. In [158]: arr = randn(6)
  2.  
  3. In [159]: arr.sort()
  4.  
  5. In [160]: arr
  6. Out[160]: array([-1.082 ,  0.3759,  0.8014,  1.1397,  1.2888,  1.8413])

在对数组进行就地排序时要注意一点：如果目标数组只是一个视图，则原始数组将会被修改：

  1. In [161]: arr = randn(3, 5)
  2.  
  3. In [162]: arr
  4. Out[162]:
  5. array([[-0.3318, -1.4711,  0.8705, -0.0847, -1.1329],
  6.        [-1.0111, -0.3436,  2.1714,  0.1234, -0.0189],
  7.        [ 0.1773,  0.7424,  0.8548,  1.038 , -0.329 ]])
  8.  
  9. In [163]: arr[:, 0].sort()  # Sort first column values in-place
  10.  
  11. In [164]: arr
  12. Out[164]:
  13. array([[-1.0111, -1.4711,  0.8705, -0.0847, -1.1329],
  14.        [-0.3318, -0.3436,  2.1714,  0.1234, -0.0189],
  15.        [ 0.1773,  0.7424,  0.8548,  1.038 , -0.329 ]])

相反，numpy.sort会为原数组创建一个已排序副本。它所接受的参数（比如kind，稍后介绍）跟ndarray.sort一样：

  1. In [165]: arr = randn(5)
  2.  
  3. In [166]: arr
  4. Out[166]: array([-1.1181, -0.2415, -2.0051,  0.7379, -1.0614])
  5.  
  6. In [167]: np.sort(arr)
  7. Out[167]: array([-2.0051, -1.1181, -1.0614, -0.2415,  0.7379])
  8.  
  9. In [168]: arr
  10. Out[168]: array([-1.1181, -0.2415, -2.0051,  0.7379, -1.0614])

这两个排序方法都可以接受一个axis参数，以便沿指定轴向对各块数据进行单独排序：

  1. In [169]: arr = randn(3, 5)
  2.  
  3. In [170]: arr
  4. Out[170]:
  5. array([[ 0.5955, -0.2682,  1.3389, -0.1872,  0.9111],
  6.        [-0.3215,  1.0054, -0.5168,  1.1925, -0.1989],
  7.        [ 0.3969, -1.7638,  0.6071, -0.2222, -0.2171]])
  8.  
  9. In [171]: arr.sort(axis=1)
  10.  
  11. In [172]: arr
  12. Out[172]:
  13. array([[-0.2682, -0.1872,  0.5955,     0.9111,   1.3389],
  14.        [-0.5168, -0.3215, -0.1989,     1.0054,   1.1925],
  15.        [-1.7638, -0.2222, -0.2171,     0.3969,   0.6071]])

你可能注意到了，这两个排序方法都不可以被设置为降序。其实这也无所谓，因为数组切片会产生视图（也就是说，不会产生副本，也不需要任何其他的计算工作）。许多Python用户都很熟悉一个有关列表的小技巧：values[::-1]可以返回一个反序的列表。对ndarray也是如此：

  1. In [173]: arr[:, ::-1]
  2. Out[173]:
  3. array([[ 1.3389,  0.9111,  0.5955, -0.1872, -0.2682],
  4.        [ 1.1925,  1.0054, -0.1989, -0.3215, -0.5168],
  5.        [ 0.6071,  0.3969, -0.2171, -0.2222, -1.7638]])

间接排序：argsort和lexsort

在数据分析工作中，常常需要根据一个或多个键对数据集进行排序。例如，一个有关学生信息的数据表可能需要以姓和名进行排序（先姓后名）。这就是间接排序的一个例子，如果你阅读过有关pandas的章节，那就已经见过不少高级例子了。给定一个或多个键，你就可以得到一个由整数组成的索引数组（我亲切地称之为索引器），其中的索引值说明了数据在新顺序下的位置。argsort和numpy.lexsort就是实现该功能的两个主要方法。下面是一个简单的例子：

  1. In [174]: values = np.array([5, 0, 1, 3, 2])
  2.  
  3. In [175]: indexer = values.argsort()
  4.  
  5. In [176]: indexer
  6. Out[176]: array([1, 2, 4, 3, 0])
  7.  
  8. In [177]: values[indexer]
  9. Out[177]: array([0, 1, 2, 3, 5])

下面这段代码根据数组的第一行对其进行排序：

  1. In [178]: arr = randn(3, 5)
  2.  
  3. In [179]: arr[0] = values
  4.  
  5. In [180]: arr
  6. Out[180]:
  7. array([[ 5.    ,  0.    ,  1.    ,  3.    ,  2.    ],
  8.        [-0.3636, -0.1378,  2.1777, -0.4728,  0.8356],
  9.        [-0.2089,  0.2316,  0.728 , -1.3918,  1.9956]])
  10.  
  11. In [181]: arr[:, arr[0].argsort()]
  12. Out[181]:
  13. array([[ 0.    ,  1.    ,   2.    ,  3.    ,  5.    ],
  14.        [-0.1378,  2.1777,   0.8356, -0.4728, -0.3636],
  15.        [ 0.2316,  0.728 ,   1.9956, -1.3918, -0.2089]])

lexsort跟argsort差不多，只不过它可以一次性对多个键数组执行间接排序（字典序）。假设我们想对一些以姓和名标识的数据进行排序：

  1. In [182]: first_name = np.array(['Bob', 'Jane', 'Steve', 'Bill', 'Barbara'])
  2.  
  3. In [183]: last_name = np.array(['Jones', 'Arnold', 'Arnold', 'Jones', 'Walters'])
  4.  
  5. In [184]: sorter = np.lexsort((first_name, last_name))
  6.  
  7. In [185]: zip(last_name[sorter], first_name[sorter])
  8. Out[185]:
  9. [('Arnold', 'Jane'),
  10.  ('Arnold', 'Steve'),
  11.  ('Jones', 'Bill'),
  12.  ('Jones', 'Bob'),
  13.  ('Walters', 'Barbara')]

刚开始使用lexsort的时候可能会比较容易头晕，这是因为键的应用顺序是从最后一个传入的算起的。不难看出，last_name是先于first_name被应用的。

注意： Series和DataFrame的sort_index以及Series的order方法就是通过这些函数的变体（它们还必须考虑缺失值）实现的。

其他排序算法

稳定的（stable）排序算法会保持等价元素的相对位置。对于相对位置具有实际意义的那些间接排序而言，这一点非常重要：

  1. In [186]: values = np.array(['2:first', '2:second', '1:first', '1:second', '1:third'])
  2.  
  3. In [187]: key = np.array([2, 2, 1, 1, 1])
  4.  
  5. In [188]: indexer = key.argsort(kind='mergesort')
  6.  
  7. In [189]: indexer
  8. Out[189]: array([2, 3, 4, 0, 1])
  9.  
  10. In [190]: values.take(indexer)
  11. Out[190]:
  12. array(['1:first', '1:second', '1:third', '2:first', '2:second'],
  13.       dtype='|S8')

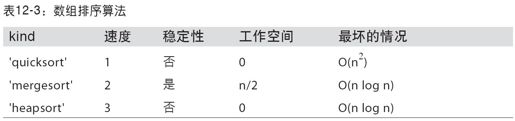
mergesort（合并排序）是唯一的稳定排序译注5，它保证有O(n log n)的性能（空间复杂度），但是其平均性能比默认的quicksort（快速排序）要差。表12-3列出了可用的排序算法及其相关的性能指标。大部分用户完全不需要知道这些东西，但了解一下总是好的。

更多有关排序的话题 - 图1

警告： 到编写本书时为止，Python对象（dtype=object）数组可用的排序算法只有quicksort。也就是说，在处理Python对象时如果需要用到稳定排序，那就得自己想办法了。

numpy.searchsorted：在有序数组中查找元素

searchsorted是一个在有序数组上执行二分查找的数组方法，只要将值插入到它返回的那个位置就能维持数组的有序性：

  1. In [191]: arr = np.array([0, 1, 7, 12, 15])
  2.  
  3. In [192]: arr.searchsorted(9)
  4. Out[192]: 3

你可能已经想到了，传入一组值就能得到一组索引：

  1. In [193]: arr.searchsorted([0, 8, 11, 16])
  2. Out[193]: array([0, 3, 3, 5])

从上面的结果中可以看出，对于元素0，searchsorted会返回0。这是因为其默认行为是返回相等值组的左侧索引：

  1. In [194]: arr = np.array([0, 0, 0, 1, 1, 1, 1])
  2.  
  3. In [195]: arr.searchsorted([0, 1])
  4. Out[195]: array([0, 3])
  5.  
  6. In [196]: arr.searchsorted([0, 1], side='right')
  7. Out[196]: array([3, 7])

再来看searchsorted的另一个用法，假设我们有一个数据数组（其中的值在0到10000之间），还有一个表示“面元边界”的数组，我们希望用它将数据数组拆分开：

  1. In [197]: data = np.floor(np.random.uniform(0, 10000, size=50))
  2.  
  3. In [198]: bins = np.array([0, 100, 1000, 5000, 10000])
  4.  
  5. In [199]: data
  6. Out[199]:
  7. array([  8304.,      4181.,       9352.,       4907.,       3250.,       8546.,       2673.,      6152.,
  8.          2774.,      5130.,       9553.,       4997.,       1794.,       9688.,       426.,       1612.,
  9.          651.,       8653.,       1695.,       4764.,       1052.,       4836.,       8020.,      3479.,
  10.          1513.,      5872.,       8992.,       7656.,       4764.,       5383.,       2319.,      4280.,
  11.          4150.,      8601.,       3946.,       9904.,       7286.,       9969.,       6032.,      4574.,
  12.          8480.,      4298.,       2708.,       7358.,       6439.,       7916.,       3899.,      9182.,
  13.          871.,       7973.])

然后，为了得到各数据点所属区间的编号（其中1表示面元[0,100)），我们可以直接使用searchsorted：

  1. In [200]: labels = bins.searchsorted(data)
  2.  
  3. In [201]: labels
  4. Out[201]:
  5. array([4, 3, 4, 3, 3, 4, 3, 4, 3, 4, 4, 3, 3, 4, 2, 3, 2, 4, 3, 3, 3, 3, 4,
  6.         3, 3, 4, 4, 4, 3, 4, 3, 3, 3, 4, 3, 4, 4, 4, 4, 3, 4, 3, 3, 4, 4, 4,
  7.         3, 4, 2, 4])

通过pandas的groupby使用该结果即可非常轻松地对原数据集进行拆分：

  1. In [202]: Series(data).groupby(labels).mean()
  2. Out[202]:
  3. 2    649.333333
  4. 3   3411.521739
  5. 4   7935.041667

注意，其实NumPy的digitize函数也可用于计算这种面元编号：

  1. In [203]: np.digitize(data, bins)
  2.  
  3. Out[203]:
  4. array([4, 3, 4, 3, 3, 4, 3, 4, 3, 4, 4, 3, 3, 4, 2, 3, 2, 4, 3, 3, 3, 3, 4,
  5.         3, 3, 4, 4, 4, 3, 4, 3, 3, 3, 4, 3, 4, 4, 4, 4, 3, 4, 3, 3, 4, 4, 4,
  6.         3, 4, 2, 4])

译注5：只是这三种里面唯一稳定的而已。