更多示例应用

本节介绍一些其他的例子。

信号前沿分析

在本小节中，我将介绍一种简化的截面动量投资组合，并告诉你如何得到模型参数化网格。首先，我将金融和技术领域中的几只股票做成一个投资组合，并加载它们的历史价格数据：

  1. names = ['AAPL', 'GOOG', 'MSFT', 'DELL', 'GS', 'MS', 'BAC', 'C']
  2. def get_px(stock, start, end):
  3.     return web.get_data_yahoo(stock, start, end)['Adj Close']
  4. px = DataFrame({n: get_px(n, '1/1/2009', '6/1/2012') for n in names})

我们可以轻松绘制每只股票的累计收益（如图11-2所示）：

  1. In [117]: px = px.asfreq('B').fillna(method='pad')
  2.  
  3. In [118]: rets = px.pct_change()
  4.  
  5. In [119]: ((1 + rets).cumprod() - 1).plot()

对于投资组合的构建，我们要计算特定回顾期的动量，然后按降序排列并标准化：

  1. def calc_mom(price, lookback, lag):
  2.     mom_ret = price.shift(lag).pct_change(lookback)
  3.     ranks = mom_ret.rank(axis=1, ascending=False)
  4.     demeaned = ranks - ranks.mean(axis=1)
  5.     return demeaned / demeaned.std(axis=1)

利用这个变换函数，我们再编写一个对策略进行事后检验的函数：通过指定回顾期和持有期（买卖之间的日数）计算投资组合整体的夏普比率。

  1. compound = lambda x : (1 + x).prod() - 1
  2. daily_sr = lambda x: x.mean() / x.std()
  3.  
  4. def strat_sr(prices, lb, hold):
  5.     # 计算投资组合权重
  6.     freq = '%dB' % hold
  7.     port = calc_mom(prices, lb, lag=1)
  8.  
  9.     daily_rets = prices.pct_change()
  10.  
  11.     # 计算投资组合收益
  12.     port = port.shift(1).resample(freq, how='first')
  13.     returns = daily_rets.resample(freq, how=compound)
  14.     port_rets = (port * returns).sum(axis=1)
  15.  
  16.     return daily_sr(port_rets) * np.sqrt(252 / hold)

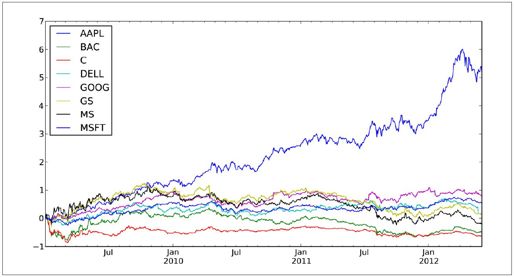
更多示例应用 - 图1

图11-2：每只股票的累计收益

通过价格数据以及一对参数组合调用该函数将会得到一个标量值：

  1. In [122]: strat_sr(px, 70, 30)
  2. Out[122]: 0.27421582756800583

然后对参数网格（即多对参数组合）应用strat_sr函数，并将结果保存在一个defaultdict中，最后再将全部结果放进一个DataFrame中：

  1. from collections import defaultdict
  2.  
  3. lookbacks = range(20, 90, 5)
  4. holdings = range(20, 90, 5)
  5. dd = defaultdict(dict)
  6. for lb in lookbacks:
  7.     for hold in holdings:
  8.         dd[lb][hold] = strat_sr(px, lb, hold)
  9. ddf = DataFrame(dd)
  10. ddf.index.name = 'Holding Period'
  11. ddf.columns.name = 'Lookback Period'

为了便于观察，我们可以将该结果图形化。下面这个函数会利用matplotlib生成一张带有装饰物译注6的热图（heatmap）：

  1. import matplotlib.pyplot as plt
  2.  
  3. def heatmap(df, cmap=plt.cm.gray_r):
  4.     fig = plt.figure()
  5.     ax = fig.add_subplot(111)
  6.     axim = ax.imshow(df.values, cmap=cmap, interpolation='nearest')
  7.     ax.set_xlabel(df.columns.name)
  8.     ax.set_xticks(np.arange(len(df.columns)))
  9.     ax.set_xticklabels(list(df.columns))
  10.     ax.set_ylabel(df.index.name)
  11.     ax.set_yticks(np.arange(len(df.index)))
  12.     ax.set_yticklabels(list(df.index))
  13.     plt.colorbar(axim)

对事后检验结果调用该函数，就会得到图11-3：

  1. In [125]: heatmap(ddf)

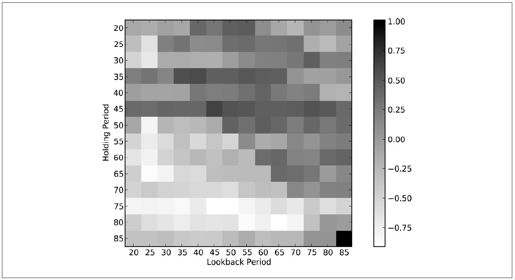
更多示例应用 - 图2

图11-3：动量策略各种回顾期和持有期的夏普比率热图（越高越好）

期货合约转仓

期货是一种无所不在的衍生品合约。它是一种在指定日期交收指定资产（比如石油、黄金或FTSE100指数的股份）的约定。在实践中，由于期货合约具有限时性，对（股票、货币、商品、债券以及其他资产类）期货合约的建模和交易是很复杂的。例如，对于某种期货（比如银或铜期货），在给定时间点，可能有多个到期时间不同的合约被交易。一般来说，下一个期满的期货合约（即近期合约）将是最具流动性的（成交量最高和买卖差价最低）。

通过一个表示盈亏（始终持有近期合约）的连续的收益指数即可轻松实现建模和预测。从一份到期合约过渡到下一期（或更远的）合约称为转仓。通过单个期货合约数据构建连续序列并不简单，而且一般都需要深入了解市场以及交易方面的知识才行。例如，你该何时以及如何快速卖出到期合约并买入下期合约？本节我所描述的就是这样的一个过程。

首先，我用SPY交易所交易基金的部分价格作为标准普尔500指数的代理：

  1. In [127]: import pandas.io.data as web
  2.  
  3. # 标准普尔500指数的近似价格
  4. In [128]: px = web.get_data_yahoo('SPY')['Adj Close'] * 10
  5.  
  6. In [129]: px
  7. Out[129]:
  8. Date
  9. 2011-08-01       1261.0
  10. 2011-08-02       1228.8
  11. 2011-08-03       1235.5
  12. ...
  13. 2012-07-25       1339.6
  14. 2012-07-26       1361.7
  15. 2012-07-27       1386.8
  16. Name: Adj Close, Length: 251

现在，稍微做一些设置。我在一个Series中放了两份标准普尔500指数期货合约及其到期日期：

  1. from datetime import datetime
  2. expiry = {'ESU2': datetime(2012, 9, 21),
  3.           'ESZ2': datetime(2012, 12, 21)}
  4. expiry = Series(expiry).order()

expiry现在应该是这个样子的：

  1. In [131]: expiry
  2. Out[131]:
  3. ESU2      2012-09-21 00:00:00
  4. ESZ2      2012-12-21 00:00:00

然后，我用Yahoo!Finance的价格以及一个随机漫步和一些噪声来模拟这两份合约未来的走势：

  1. np.random.seed(12347)
  2. N = 200
  3. walk = (np.random.randint(0, 200, size=N) - 100) * 0.25
  4. perturb = (np.random.randint(0, 20, size=N) - 10) * 0.25
  5. walk = walk.cumsum()
  6.  
  7. rng = pd.date_range(px.index[0], periods=len(px) + N, freq='B')
  8. near = np.concatenate([px.values, px.values[-1] + walk])
  9. far = np.concatenate([px.values, px.values[-1] + walk + perturb])
  10. prices = DataFrame({'ESU2': near, 'ESZ2': far}, index=rng)

这样，prices就有了关于这两个合约的时间序列：

  1. In [133]: prices.tail()
  2. Out[133]:
  3.                ESU2     ESZ2
  4. 2013-04-16  1416.05  1417.80
  5. 2013-04-17  1402.30  1404.55
  6. 2013-04-18  1410.30  1412.05
  7. 2013-04-19  1426.80  1426.05
  8. 2013-04-22  1406.80  1404.55

将多个时间序列合并为单个连续序列的一个办法是构造一个加权矩阵。活动合约的权重应该设为1，直到期满为止。在那个时候，你必须决定一个转仓约定。下面这个函数可以计算一个加权矩阵（权重根据到期前的期数减少而线性衰减）：

  1. def get_roll_weights(start, expiry, items, roll_periods=5):
  2.     # start : 用于计算加权矩阵的第一天
  3.     # expiry : 由“合约代码 -> 到期日期”组成的序列
  4.     # items : 一组合约名称
  5.  
  6.     dates = pd.date_range(start, expiry[-1], freq='B')
  7. 　　 weights = DataFrame(np.zeros((len(dates), len(items))),
  8. 　　                     index=dates, columns=items)
  9.  
  10.     prev_date = weights.index[0]
  11.     for i, (item, ex_date) in enumerate(expiry.iteritems()):
  12.         if i < len(expiry) - 1:
  13.             weights.ix[prev_date:ex_date - pd.offsets.BDay(), item] = 1
  14.             roll_rng = pd.date_range(end=ex_date - pd.offsets.BDay(),
  15.                                      periods=roll_periods + 1, freq='B')
  16.  
  17.             decay_weights = np.linspace(0, 1, roll_periods + 1)
  18.             weights.ix[roll_rng, item] = 1 - decay_weights
  19.             weights.ix[roll_rng, expiry.index[i + 1]] = decay_weights
  20.         else:
  21.             weights.ix[prev_date:, item] = 1
  22.  
  23.         prev_date = ex_date
  24.     return weights

快到ESU2到期日的那几天的权重如下所示：

  1. In [135]: weights = get_roll_weights('6/1/2012', expiry, prices.columns)
  2.  
  3. In [136]: weights.ix['2012-09-12':'2012-09-21']
  4. Out[136]:
  5.             ESU2     ESZ2
  6. 2012-09-12   1.0      0.0
  7. 2012-09-13   1.0      0.0
  8. 2012-09-14   0.8      0.2
  9. 2012-09-17   0.6      0.4
  10. 2012-09-18   0.4      0.6
  11. 2012-09-19   0.2      0.8
  12. 2012-09-20   0.0      1.0
  13. 2012-09-21   0.0      1.0

最后，转仓期货收益就是合约收益的加权和：

  1. In [137]: rolled_returns = (prices.pct_change() * weights).sum(1)

移动相关系数与线性回归

动态模型在金融建模工作中扮演着重要的角色，因为它们可用于模拟历史时期中的交易决策。移动窗口和指数加权时间序列函数就是用于处理动态模型的工具。

相关系数是观察两个资产时间序列的变化的协动性的一种手段。pandas的rolling_corr函数可以根据两个收益序列计算出移动窗口相关系数。首先，我从Yahoo!Finance加载一些价格序列，并计算每日收益率：

  1. aapl = web.get_data_yahoo('AAPL', '2000-01-01')['Adj Close']
  2. msft = web.get_data_yahoo('MSFT', '2000-01-01')['Adj Close']
  3.  
  4. aapl_rets = aapl.pct_change()
  5. msft_rets = msft.pct_change()

然后，我计算一年期移动相关系数并绘制图表（如图11-4所示）：

  1. In [140]: pd.rolling_corr(aapl_rets, msft_rets, 250).plot()

两个资产之间的相关系数存在一个问题，即它不能捕获波动性差异。最小二乘回归提供了另一种对一个变量与一个或多个其他预测变量之间动态关系的建模办法。

  1. In [142]: model = pd.ols(y=aapl_rets, x={'MSFT': msft_rets}, window=250)
  2.  
  3. In [143]: model.beta
  4. Out[143]:
  5. <class 'pandas.core.frame.DataFrame'>
  6. DatetimeIndex: 2913 entries, 2000-12-28 00:00:00 to 2012-07-27 00:00:00
  7. Data columns:
  8. MSFT         2913  non-null values
  9. intercept    2913  non-null values
  10. dtypes: float64(2)
  11.  
  12. In [144]: model.beta['MSFT'].plot()

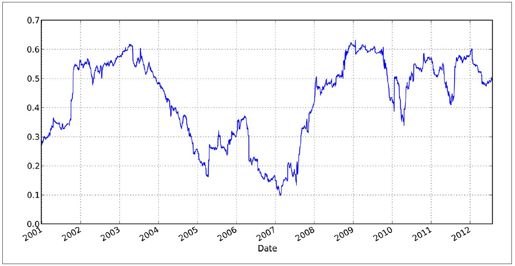
更多示例应用 - 图3

图11-4：苹果与微软的一年期相关系数

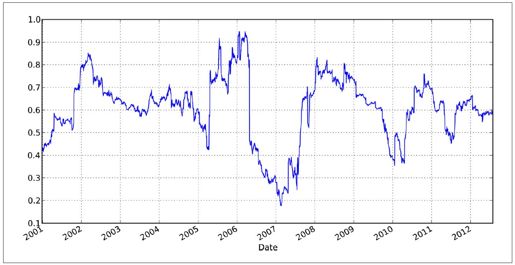
更多示例应用 - 图4

图11-5：苹果对微软一年期beta（OLS回归系数）

pandas的ols函数实现了静态和动态（扩展或移动窗口）的最小二乘回归。有关统计学和计量经济学的复杂模型的更多信息，请参考statsmodels项目（http://statsmodels.sourceforge.net）。

译注6：“装饰物”就是图例、标题之类的“配角”元素。