广播

广播（broadcasting）指的是不同形状的数组之间的算术运算的执行方式。它是一种非常强大的功能，但也容易令人误解，即使是经验丰富的老手也是如此。将标量值跟数组合并时就会发生最简单的广播：

  1. In [80]: arr = np.arange(5)
  2.  
  3. In [81]: arr                          In [82]: arr * 4
  4. Out[81]: array([0, 1, 2, 3, 4])       Out[82]: array([ 0,  4,  8, 12, 16])

这里我们说：在这个乘法运算中，标量值4被广播到了其他所有的元素上。

再来看一个例子，我们可以通过减去列平均值的方式对数组的每一列进行距平化处理。这个问题解决起来非常简单：

  1. In [83]: arr = randn(4, 3)
  2.  
  3. In [84]: arr.mean(0)
  4. Out[84]: array([ 0.1321,  0.552 ,  0.8571])
  5.  
  6. In [85]: demeaned = arr - arr.mean(0)
  7.  
  8. In [86]: demeaned                          In [87]: demeaned.mean(0)
  9. Out[86]:                                   Out[87]: array([ 0., -0., -0.])
  10. array([[ 0.1718, -0.1972, -1.3669],
  11.        [ -0.1292,  1.6529, -0.3429],
  12.        [ -0.2891, -0.0435,  1.2322],
  13.        [ 0.2465, -1.4122,  0.4776]])

图12-4形象地展示了该过程。用广播的方式对行进行距平化处理会稍微麻烦一些。幸运的是，只要遵循一定的规则，低维度的值是可以被广播到数组的任意维度的（比如对二维数组各列减去行平均值）。于是就得到了：

广播 - 图1

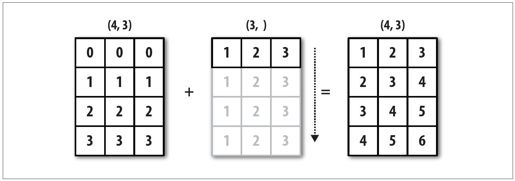
图12-4：一维数组在轴0上的广播

广播 - 图2

虽然我是一名经验丰富的NumPy老手，但经常还是得停下来画张图并想想广播的原则。再来看一下最后那个例子，假设你希望对各行减去那个平均值。由于arr.mean(0)的长度为3，所以它可以在0轴向上进行广播：因为arr的后缘维度是3，所以它们是兼容的。根据该原则，要在1轴向上做减法（即各行减去行平均值），较小的那个数组的形状必须是(4,1)：

  1. In [88]: arr
  2. Out[88]:
  3. array([[ 0.3039,  0.3548, -0.5097],
  4.        [ 0.0029,  2.2049,  0.5142],
  5.        [ -0.1571,  0.5085,  2.0893],
  6.        [ 0.3786, -0.8602,  1.3347]])
  7.  
  8. In [89]: row_means = arr.mean(1)       In [90]: row_means.reshape((4, 1))
  9.                                        Out[90]:
  10.                                        array([[ 0.0496],
  11.                                               [ 0.9073],
  12.                                               [ 0.8136],
  13.                                               [ 0.2844]])
  14.  
  15. In [91]: demeaned = arr - row_means.reshape((4, 1))
  16.  
  17. In [92]: demeaned.mean(1)
  18. Out[92]: array([ 0.,  0.,  0.,  0.])

你的头还没炸吧？图12-5说明了该运算的过程。

广播 - 图3

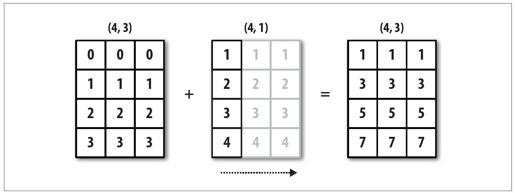
图12-5：二维数组在轴1上的广播

图12-6展示了另外一种情况，这次是在一个三维数组上沿0轴向加上一个二维数组。

广播 - 图4

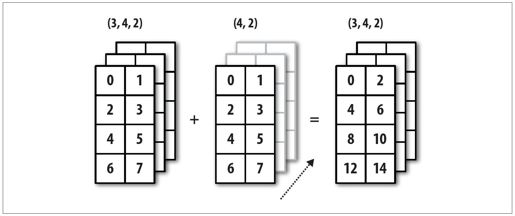
图12-6：三维数组在轴0上的广播

沿其他轴向广播

高维度数组的广播似乎更难以理解，而实际上它也是遵循广播原则的。如果不然，你就会得到下面这样一个错误：

  1. In [93]: arr - arr.mean(1)

ValueError Traceback (most recent call last) <ipython-input-93-7b87b85a20b2> in <module>() ——> 1 arr - arr.mean(1) ValueError: operands could not be broadcast together with shapes (4,3) (4)

人们经常需要通过算术运算过程将较低维度的数组在除0轴以外的其他轴向上广播。根据广播的原则，较小数组的“广播维”必须为1。在上面那个行距平化的例子中，这就意味着要将行平均值的形状变成(4,1)而不是(4,)：

  1. In [94]: arr - arr.mean(1).reshape((4, 1))
  2. Out[94]:
  3. array([[ 0.2542,  0.3051, -0.5594],
  4.        [ -0.9044,  1.2976, -0.3931],
  5.        [ -0.9707, -0.3051,  1.2757],
  6.        [ 0.0942, -1.1446,  1.0503]])

对于三维的情况，在三维中的任何一维上广播其实也就是将数据重塑为兼容的形状而已。图12-7说明了要在三维数组各维度上广播的形状需求。

广播 - 图5

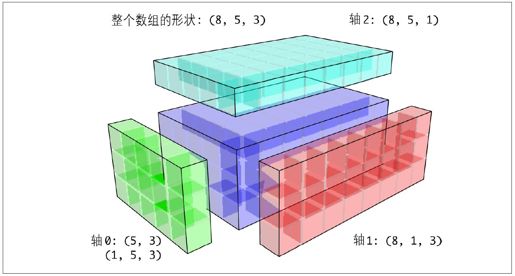
图12-7：能在该三维数组上广播的二维数组的形状

于是就有了一个非常普遍的问题（尤其是在通用算法中），即专门为了广播而添加一个长度为1的新轴。虽然reshape是一个办法，但插入轴需要构造一个表示新形状的元组。这是一个很郁闷的过程。因此，NumPy数组提供了一种通过索引机制插入轴的特殊语法。下面这段代码通过特殊的np.newaxis属性以及“全”切片来插入新轴：

  1. In [95]: arr = np.zeros((4, 4))
  2.  
  3. In [96]: arr_3d = arr[:, np.newaxis, :]
  4.  
  5. In [97]: arr_3d.shape
  6. Out[97]: (4, 1, 4)
  7.  
  8. In [98]: arr_1d = np.random.normal(size=3)
  9.  
  10. In [99]: arr_1d[:, np.newaxis]       In [100]: arr_1d[np.newaxis, :]
  11. Out[99]:                             Out[100]: array([[-0.3899,  0.396 , -0.1852]])
  12. array([[-0.3899],
  13.        [ 0.396 ],
  14.        [ -0.1852]])

因此，如果我们有一个三维数组，并希望对轴2进行距平化，那么只需要编写下面这样的代码就可以了：

  1. In [101]: arr = randn(3, 4, 5)
  2.  
  3. In [102]: depth_means = arr.mean(2)
  4.  
  5. In [103]: depth_means
  6. Out[103]:
  7. array([[ 0.1097,  0.3118, -0.5473,  0.2663],
  8.        [ 0.1747,  0.1379,  0.1146, -0.4224],
  9.        [ 0.0217,  0.3686, -0.0468,  1.3026]])
  10.  
  11. In [104]: demeaned = arr - depth_means[:, :, np.newaxis]
  12.  
  13. In [105]: demeaned.mean(2)
  14. Out[105]:
  15. array([[ 0.,  0., -0.,  0.],
  16.        [ 0., -0., -0.,  0.],
  17.        [ -0., -0.,  0.,  0.]])

也许你会对此感到非常困惑。不用担心，只要多动手，很快就能搞明白！

有些读者可能会想，在对指定轴进行距平化时，有没有一种既通用又不牺牲性能的方法呢？实际上是有的，但需要一些索引方面的技巧：

  1. def demean_axis(arr, axis=0):
  2.     means = arr.mean(axis)
  3.  
  4.     # 下面这些一般化的东西类似于N维的[:, :, np.newaxis]
  5.     indexer = [slice(None)] * arr.ndim
  6.     indexer[axis] = np.newaxis
  7.     return arr - means[indexer]

通过广播设置数组的值

算术运算所遵循的广播原则同样也适用于通过索引机制设置数组值的操作。对于最简单的情况，我们可以这样做：

  1. In [106]: arr = np.zeros((4, 3))
  2.  
  3. In [107]: arr[:] = 5           In [108]: arr
  4.                                Out[108]:
  5.                                array([[ 5.,  5.,  5.],
  6.                                       [ 5.,  5.,  5.],
  7.                                       [ 5.,  5.,  5.],
  8.                                       [ 5.,  5.,  5.]])

再看一个复杂点的例子，假设我们想要用一个一维数组来设置目标数组的各列。只要保证形状兼容就可以了：

  1. In [109]: col = np.array([1.28, -0.42, 0.44, 1.6])
  2.  
  3. In [110]: arr[:] = col[:, np.newaxis]          In [111]: arr
  4.                                                Out[111]:
  5.                                                array([[ 1.28,  1.28,  1.28],
  6.                                                       [ -0.42, -0.42, -0.42],
  7.                                                       [ 0.44,  0.44,  0.44],
  8.                                                       [ 1.6 ,  1.6 ,  1.6 ]])
  9.  
  10. In [112]: arr[:2] = [[-1.37], [0.509]]         In [113]: arr
  11.                                                Out[113]:
  12.                                                array([[-1.37 , -1.37 , -1.37 ],
  13.                                                       [ 0.509,  0.509,  0.509],
  14.                                                       [ 0.44 ,  0.44 ,  0.44 ],
  15.                                                       [ 1.6  ,  1.6  ,  1.6  ]])