移动窗口函数

在移动窗口（可以带有指数衰减权数）上计算的各种统计函数也是一类常见于时间序列的数组变换。我将它们称为移动窗口函数（moving window function），其中还包括那些窗口不定长的函数（如指数加权移动平均）。跟其他统计函数一样，移动窗口函数也会自动排除缺失值。

rolling_mean是其中最简单的一个。它接受一个TimeSeries或DataFrame以及一个window（表示期数）：

  1. In [555]: close_px.AAPL.plot()
  2. Out[555]: <matplotlib.axes.AxesSubplot at 0x1099b3990>
  3.  
  4. In [556]: pd.rolling_mean(close_px.AAPL, 250).plot()

结果如图10-8所示。默认情况下，诸如rolling_mean这样的函数需要指定数量译注8的非NA观测值。可以修改该行为以解决缺失数据的问题。其实，在时间序列开始处尚不足窗口期的那些数据就是个特例（见图10-9）：

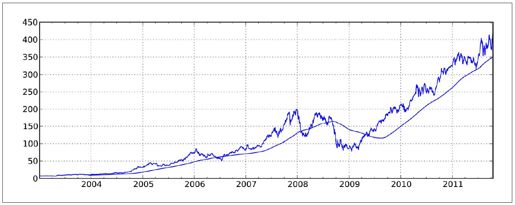
移动窗口函数 - 图1

图10-8：苹果公司股价的250日均线

  1. In [558]: appl_std250 = pd.rolling_std(close_px.AAPL, 250, min_periods=10)
  2.  
  3. In [559]: appl_std250[5:12]
  4. Out[559]:
  5. 2003-01-09         NaN
  6. 2003-01-10         NaN
  7. 2003-01-13         NaN
  8. 2003-01-14         NaN
  9. 2003-01-15    0.077496
  10. 2003-01-16    0.074760
  11. 2003-01-17    0.112368
  12. Freq: B
  13.  
  14. In [560]: appl_std250.plot()

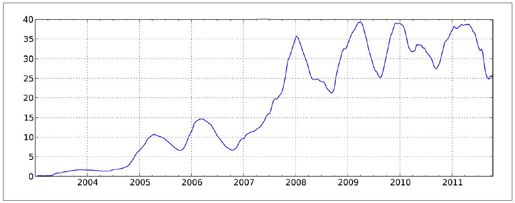
移动窗口函数 - 图2

图10-9：苹果公司250日每日回报标准差

要计算扩展窗口平均（expanding window mean），你可以将扩展窗口看做一个特殊的窗口，其长度与时间序列一样，但只需一期（或多期译注9）即可计算一个值：

  1. # 通过rolling_mean定义扩展平均
  2. In [561]: expanding_mean = lambda x: rolling_mean(x, len(x), min_periods=1)

对DataFrame调用rolling_mean（以及与之类似的函数）会将转换应用到所有的列上（见图10-10）：

  1. In [563]: pd.rolling_mean(close_px, 60).plot(logy=True)

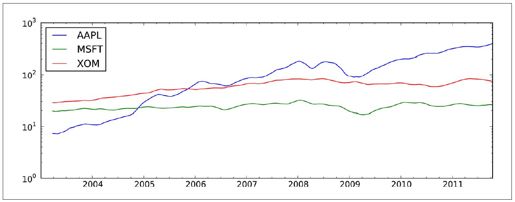
移动窗口函数 - 图3

图10-10：各股价60日均线（对数Y轴）

表10-6中列出了pandas中的此类函数。

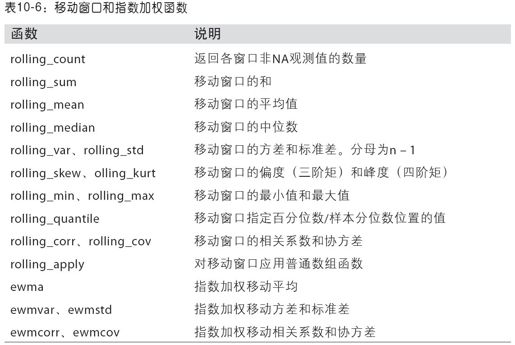
移动窗口函数 - 图4

注意： bottleneck（由Keith Goodman制作的Python库）提供了另一种对NaN友好的移动窗口函数集。值得一看，说不定能在你的工作中派上用场。

指数加权函数

另一种使用固定大小窗口及相等权数观测值的办法是，定义一个衰减因子（decay factor）常量，以便使近期的观测值拥有更大的权数。用数学术语来讲，如果mat是时间t的移动平均结果，x是时间序列，结果中的各个值可用mat =amat-1+(a -1)x-t进行计算，其中a为衰减因子。衰减因子的定义方式有很多，比较流行的是使用时间间隔（span），它可以使结果兼容于窗口大小等于时间间隔的简单移动窗口（simple moving window）函数。

由于指数加权统计会赋予近期的观测值更大的权数，因此相对于等权统计译注10，它能“适应”更快的变化。下面这个例子对比了苹果公司股价的60日移动平均和span=60的指数加权移动平均（如图10-11所示）：

  1. fig, axes = plt.subplots(nrows=2, ncols=1, sharex=True, sharey=True, figsize=(12, 7))
  2.  
  3. aapl_px = close_px.AAPL['2005':'2009']
  4.  
  5. ma60 = pd.rolling_mean(aapl_px, 60, min_periods=50)
  6. ewma60 = pd.ewma(aapl_px, span=60)
  7.  
  8. aapl_px.plot(style='k-', ax=axes[0])
  9. ma60.plot(style='k--', ax=axes[0])
  10. aapl_px.plot(style='k-', ax=axes[1])
  11. ewma60.plot(style='k--', ax=axes[1])
  12. axes[0].set_title('Simple MA')
  13. axes[1].set_title('Exponentially-weighted MA')

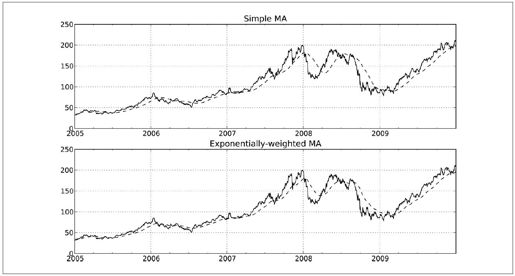
移动窗口函数 - 图5

图10-11：简单移动平均与指数加权移动平均

二元移动窗口函数

有些统计运算（如相关系数和协方差）需要在两个时间序列上执行。例如，金融分析师常常对某只股票对某个参考指数（如标准普尔500指数）的相关系数感兴趣。我们可以通过计算百分数变化并使用rolling_corr的方式得到该结果（如图10-12所示）：

  1. In [569]: spx_px = close_px_all ['SPX']
  2.  
  3. In [570]: spx_rets = spx_px / spx_px.shift(1) - 1
  4.  
  5. In [571]: returns = close_px.pct_change()
  6.  
  7. In [572]: corr = pd.rolling_corr(returns.AAPL, spx_rets, 125, min_periods=100)
  8.  
  9. In [573]: corr.plot()

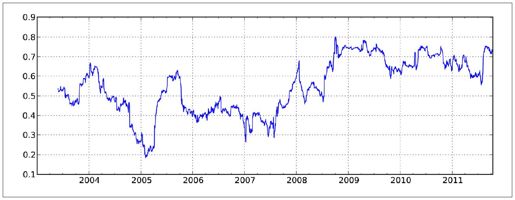
移动窗口函数 - 图6

图10-12：AAPL 6个月的回报与标准普尔500指数的相关系数

假设你想要一次性计算多只股票与标准普尔500指数的相关系数。虽然编写一个循环并新建一个DataFrame不是什么难事，但比较唆。其实，只需传入一个TimeSeries和一个DataFrame，rolling_corr就会自动计算TimeSeries（本例中就是spx_rets）与DataFrame各列的相关系数。结果如图10-13所示：

  1. In [575]: corr = pd.rolling_corr(returns, spx_rets, 125, min_periods=100)
  2.  
  3. In [576]: corr.plot()

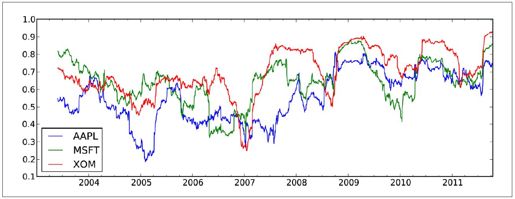
移动窗口函数 - 图7

图10-13：3只股票6个月的回报与标准普尔500指数的相关系数

用户定义的移动窗口函数

rolling_apply函数使你能够在移动窗口上应用自己设计的数组函数。唯一要求的就是：该函数要能从数组的各个片段中产生单个值（即约简）。比如说，当我们用rolling_quantile计算样本分位数时，可能对样本中特定值的百分等级感兴趣。scipy.stats.percentileofscore函数就能达到这个目的：

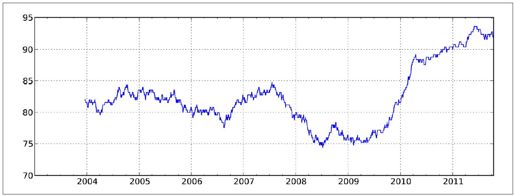
移动窗口函数 - 图8

图10-14：AAPL 2%回报率的百分等级（一年窗口期）

  1. In [578]: from scipy.stats import percentileofscore
  2.  
  3. In [579]: score_at_2percent = lambda x: percentileofscore(x, 0.02)
  4.  
  5. In [580]: result = pd.rolling_apply(returns.AAPL, 250, score_at_2percent)
  6.  
  7. In [581]: result.plot()

译注8：这是针对窗口而言的，即一个窗口里面必须有多少个非NA值。

译注9：不设置就全空，也不要太大，大了就无意义了。

译注10：就是不加权的普通移动平均。