pandas中的绘图函数

不难看出，matplotlib实际上是一种比较低级的工具。要组装一张图表，你得用它的各种基础组件才行：数据展示（即图表类型：线型图、柱状图、盒形图、散布图、等值线图等）、图例、标题、刻度标签以及其他注解型信息。这是因为要根据数据制作一张完整图表通常都需要用到多个对象。在pandas中，我们有行标签、列标签以及分组信息（可能有）。这也就是说，要制作一张完整的图表，原本需要一大堆的matplotlib代码，现在只需一两条简洁的语句就可以了。pandas有许多能够利用DataFrame对象数据组织特点来创建标准图表的高级绘图方法（这些函数的数量还在不断增加）。

警告： 到目前为止，pandas团队已经在绘图功能上下了很大工夫。一个参加了“2012Google Summer of Code计划”的学生正在夜以继日地添加新功能，并使该接口具有更好的一致性和可用性。因此，本书中的这部分代码可能很快就要过时了。如果那样的话，pandas在线文档将会是最好的学习资源。

线型图

Series和DataFrame都有一个用于生成各类图表的plot方法。默认情况下，它们所生成的是线型图（如图8-13所示）：

  1. In [55]: s = Series(np.random.randn(10).cumsum(), index=np.arange(0, 100, 10))
  2.  
  3. In [56]: s.plot()

该Series对象的索引会被传给matplotlib，并用以绘制X轴。可以通过use_index=False禁用该功能。X轴的刻度和界限可以通过xticks和xlim选项进行调节，Y轴就用yticks和ylim。plot参数的完整列表请参见表8-3。我只会讲解其中几个，剩下的就留给读者自己去研究了。

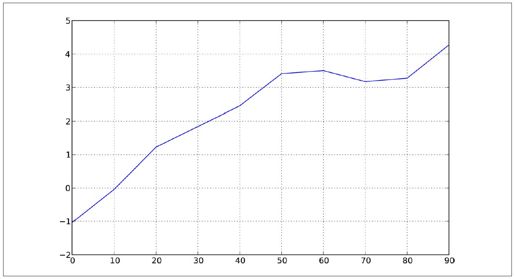
pandas中的绘图函数 - 图1

图8-13：简单的Series图表示例

pandas的大部分绘图方法都有一个可选的ax参数，它可以是一个matplotlib的subplot对象。这使你能够在网格布局中更为灵活地处理subplot的位置。

DataFrame的plot方法会在一个subplot中为各列绘制一条线，并自动创建图例（如图8-14所示）：

  1. In [57]: df = DataFrame(np.random.randn(10, 4).cumsum(0),
  2.     ...:                columns=['A', 'B', 'C', 'D'],
  3.     ...:                index=np.arange(0, 100, 10))
  4.  
  5. In [58]: df.plot()

注意： plot的其他关键字参数会被传给相应的matplotlib绘图函数，所以要更深入地自定义图表，就必须学习更多有关matplotlib API的知识。

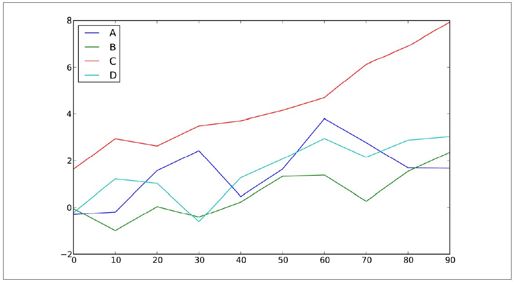
pandas中的绘图函数 - 图2

图8-14：简单的DataFrame图表示例

pandas中的绘图函数 - 图3

pandas中的绘图函数 - 图4

DataFrame还有一些用于对列进行灵活处理的选项，例如，是要将所有列都绘制到一个subplot中还是创建各自的subplot。详细信息请参见表8-4。

pandas中的绘图函数 - 图5

注意： 有关时间序列的绘制技术，请参见第10章。

柱状图

在生成线型图的代码中加上kind='bar'（垂直柱状图）或kind='barh'（水平柱状图）即可生成柱状图。这时，Series和DataFrame的索引将会被用作X（bar）或Y（barh）刻度（如图8-15所示）：

  1. In [59]: fig, axes = plt.subplots(2, 1)
  2.  
  3. In [60]: data = Series(np.random.rand(16), index=list('abcdefghijklmnop'))
  4.  
  5. In [61]: data.plot(kind='bar', ax=axes[0], color='k', alpha=0.7)
  6. Out[61]: <matplotlib.axes.AxesSubplot at 0x4ee7750>
  7.  
  8. In [62]: data.plot(kind='barh', ax=axes[1], color='k', alpha=0.7)

注意： 更多有关plt.subplots函数以及matplotlib轴和图像的信息，请参见本章后续的内容。

对于DataFrame，柱状图会将每一行的值分为一组，如图8-16所示：

  1. In [63]: df = DataFrame(np.random.rand(6, 4),
  2.     ...:                index=['one', 'two', 'three', 'four', 'five', 'six'],
  3.     ...:                columns=pd.Index(['A', 'B', 'C', 'D'], name='Genus'))
  4.  
  5. In [64]: df
  6. Out[64]:
  7. Genus          A              B         C         D
  8. one     0.301686       0.156333  0.371943  0.270731
  9. two     0.750589       0.525587  0.689429  0.358974
  10. three   0.381504       0.667707  0.473772  0.632528
  11. four    0.942408       0.180186  0.708284  0.641783
  12. five    0.840278       0.909589  0.010041  0.653207
  13. six     0.062854       0.589813  0.811318  0.060217
  14.  
  15. In [65]: df.plot(kind='bar')

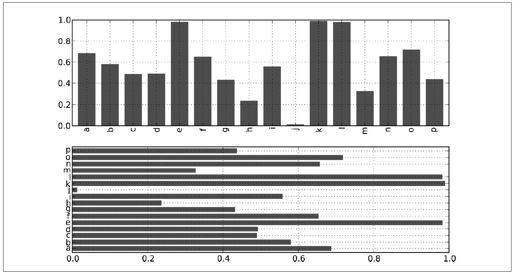
pandas中的绘图函数 - 图6

图8-15：水平和垂直柱状图示例

注意，DataFrame各列的名称"Genus"被用作了图例的标题。设置stacked=True即可为DataFrame生成堆积柱状图，这样每行的值就会被堆积在一起（如图8-17所示）：

  1. In [67]: df.plot(kind='barh', stacked=True, alpha=0.5)

注意： 柱状图有一个非常不错的用法：利用value_counts图形化显示Series中各值的出现频率，比如s.value_counts ().plot(kind='bar')。

再以本书前面用过的那个有关小费的数据集为例译注3，假设我们想要做一张堆积柱状图以展示每天各种聚会规模的数据点的百分比。我用read_csv将数据加载进来，然后根据日期和聚会规模创建一张交叉表：

  1. In [68]: tips = pd.read_csv('ch08/tips.csv')
  2.  
  3. In [69]: party_counts = pd.crosstab(tips.day, tips.size)
  4.  
  5. In [70]: party_counts
  6. Out[70]:
  7. size  1   2   3   4  5  6
  8. day
  9. Fri   1  16   1   1  0  0
  10. Sat   2  53  18  13  1  0
  11. Sun   0  39  15  18  3  1
  12. Thur  1  48   4   5  1  3
  13.  
  14. # 1个人和6个人的聚会都比较少
  15. In [71]: party_counts = party_counts.ix[:, 2:5]

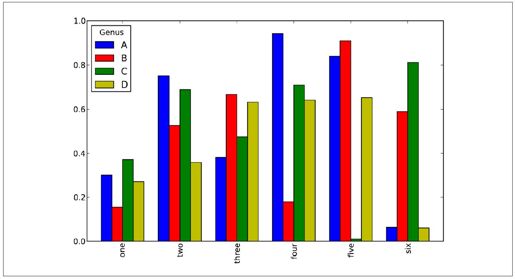
pandas中的绘图函数 - 图7

图8-16：DataFrame柱状图示例

pandas中的绘图函数 - 图8

图8-17：DataFrame堆积柱状图示例

然后进行规格化，使得各行的和为1（必须转换成浮点数，以避免Python 2.7中的整数除法问题），并生成图表（如图8-18所示）：

  1. # 规格化成“和为1”
  2. In [72]: party_pcts = party_counts.div(party_counts.sum(1).astype(float), axis=0)
  3.  
  4. In [73]: party_pcts
  5. Out[73]:
  6. size          2             3         4         5
  7. day
  8. Fri    0.888889      0.055556  0.055556  0.000000
  9. Sat    0.623529      0.211765  0.152941  0.011765
  10. Sun    0.520000      0.200000  0.240000  0.040000
  11. Thur   0.827586      0.068966  0.086207  0.017241
  12. In [74]: party_pcts.plot(kind='bar', stacked=True)

于是，通过该数据集就可以看出，聚会规模在周末会变大。

直方图和密度图

直方图（histogram）是一种可以对值频率进行离散化显示的柱状图。数据点被拆分到离散的、间隔均匀的面元中，绘制的是各面元中数据点的数量。再以前面那个小费数据为例，通过Series的hist方法，我们可以生成一张“小费占消费总额百分比”译注4的直方图（如图8-19所示）：

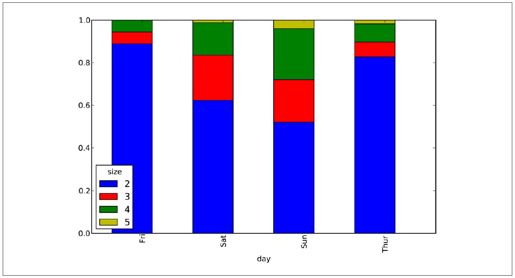
pandas中的绘图函数 - 图9

图8-18：每天各种聚会规模的比例

  1. In [76]: tips['tip_pct'] = tips['tip'] / tips['total_bill']
  2.  
  3. In [77]: tips['tip_pct'].hist(bins=50)

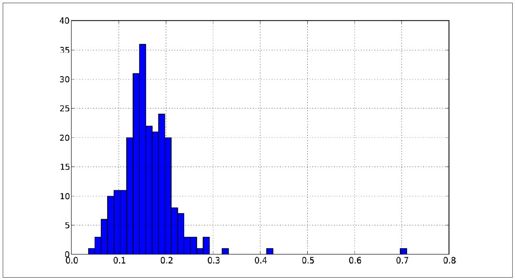
pandas中的绘图函数 - 图10

图8-19：小费百分比的直方图

与此相关的一种图表类型是密度图，它是通过计算“可能会产生观测数据的连续概率分布的估计”而产生的。一般的过程是将该分布近似为一组核（即诸如正态（高斯）分布之类的较为简单的分布）。因此，密度图也被称作KDE（Kernel Density Estimate，核密度估计）图。调用plot时加上kind='kde'即可生成一张密度图（标准混合正态分布KDE），如图8-20所示：

  1. In [79]: tips['tip_pct'].plot(kind='kde')

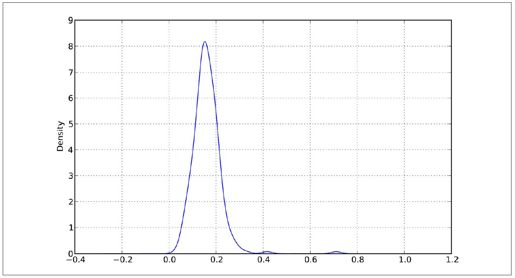
pandas中的绘图函数 - 图11

图8-20：小费百分比的密度图

这两种图表常常会被画在一起。直方图以规格化形式给出（以便给出面元化密度），然后再在其上绘制核密度估计。接下来来看一个由两个不同的标准正态分布组成的双峰分布（如图8-21所示）：

  1. In [81]: comp1 = np.random.normal(0, 1, size=200)  # N(0, 1)
  2.  
  3. In [82]: comp2 = np.random.normal(10, 2, size=200)  # N(10, 4)
  4. In [83]: values = Series(np.concatenate([comp1, comp2]))
  5.  
  6. In [84]: values.hist(bins=100, alpha=0.3, color='k', normed=True)
  7. Out[84]: <matplotlib.axes.AxesSubplot at 0x5cd2350>
  8.  
  9. In [85]: values.plot(kind='kde', style='k--')

散布图

散布图（scatter plot）是观察两个一维数据序列之间的关系的有效手段。matplotlib的scatter方法是绘制散布图的主要方法。在下面这个例子中，我加载了来自statsmodels项目的macrodata数据集，选择其中几列，然后计算对数差：

  1. In [86]: macro = pd.read_csv('ch08/macrodata.csv')
  2.  
  3. In [87]: data = macro[['cpi', 'm1', 'tbilrate', 'unemp']]
  4.  
  5. In [88]: trans_data = np.log(data).diff().dropna()
  6.  
  7. In [89]: trans_data[-5:]
  8. Out[89]:
  9.           cpi        m1  tbilrate     unemp
  10. 198 -0.007904  0.045361 -0.396881  0.105361
  11. 199 -0.021979  0.066753 -2.277267  0.139762
  12. 200  0.002340  0.010286  0.606136  0.160343
  13. 201  0.008419  0.037461 -0.200671  0.127339
  14. 202  0.008894  0.012202 -0.405465  0.042560

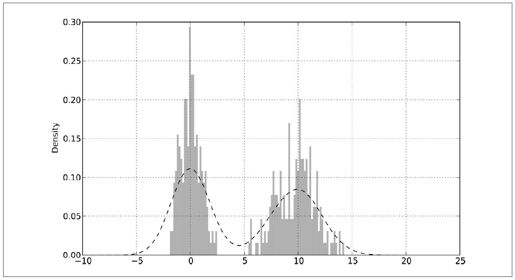
pandas中的绘图函数 - 图12

图8-21：带有密度估计的规格化直方图

利用plt.scatter即可轻松绘制一张简单的散布图（如图8-22所示）：

  1. In [91]: plt.scatter(trans_data['m1'], trans_data['unemp'])
  2. Out[91]: <matplotlib.collections.PathCollection at 0x43c31d0>
  3.  
  4. In [92]: plt.title('Changes in log %s vs. log %s' % ('m1', 'unemp'))

在探索式数据分析工作中，同时观察一组变量的散布图是很有意义的，这也被称为散布图矩阵（scatter plot matrix）。纯手工创建这样的图表很费工夫，所以pandas提供了一个能从DataFrame创建散布图矩阵的scatter_matrix函数。它还支持在对角线上放置各变量的直方图或密度图。结果如图8-23所示：

  1. In [93]: pd.scatter_matrix(trans_data, diagonal='kde', color='k', alpha=0.3)

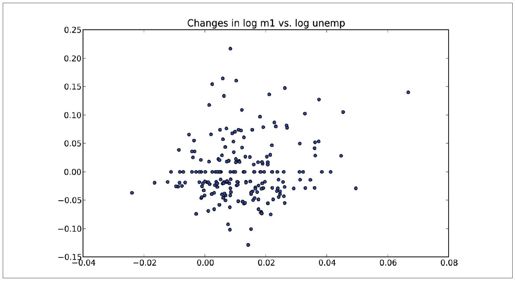
pandas中的绘图函数 - 图13

图8-22：一张简单的散布图

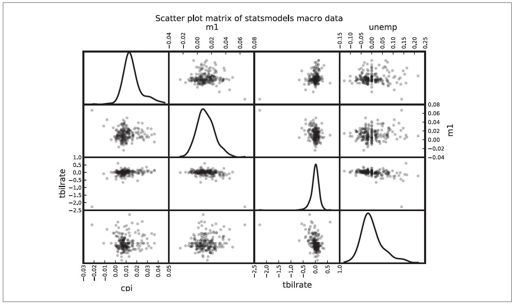
pandas中的绘图函数 - 图14

图8-23：statsmodels macro data的散布图矩阵

译注3：本书前面没有用过这个数据集，读者不用找了。

译注4：仔细观察数据可以发现，实际并不是这样的，因为这里的小费可能不在消费总额里面。仅仅当做一个例子即可，不必深究。