1.1 环游美国之旅

TSP虽然公认棘手，但从某一方面来看却相当容易：经过给定一组城市的全部可能路线总数是有限的，因此1962年的某位数学家只需检验每条可能的路线，将最短的一条记录下来寄给宝洁公司，便可坐等一万美元支票寄到家中。这个解题策略堪称简单而完美，但有一点潜在的困难。由于路线总数极其庞大，根本不可能逐一检验。

1930年，奥地利数学家、经济学家Karl Menger已注意到TSP存在这种困难。最初正是因为他的工作，数学界才开始关注TSP这道难题。他写道：“该问题当然可以在有限多次试验内解决，但是尚未发现能够给出比给定点的全排列数更低的试验次数的解法。”¹一条路线可以通过到达各城市的顺序来唯一确定。我们依次用字母A～Z及数字1～7表示Toody和Muldoon的33个目的地，即A代表芝加哥市，B代表维奇托市，以此类推。如此，一条可能的路线便可以记作

ABCDEFGHIJKLMNOPQRSTUVWXYZ1234567

或以上符号排成其他任一序列的形式。每一个这样的序列都是这33个符号的一个排列（permutation）。

_{1. Menger (1931).}

由于旅行的起点和终点相同，每个排列对应的路线实际都是一条环形路线，在这条环形路线上选择另外一座城市作为起点就能得到另一个不同的序列，因此同一条环形路线对应33个不同的线性排列。为避免重复计数，不妨固定城市A为每条路线的起点，则第二座城市有32种可能选择，第三座城市有31种可能选择，以此类推。最后，可以得到环形路线的总数为32×31×30×…×3×2×1。这个数字记作32!，读作32的阶乘，表示32个不同物体总共有多少种排列情况，也称为全排列数。

在“54号车”竞赛题中，注意到从芝加哥到维奇托的距离等于从维奇托到芝加哥的距离，并且对于任意两座城市来说都是如此，所以我们可以减少一部分工作量。根据对称性，对于同一条路线，总路程与旅行方向无关。因此，字符串

ABCDEFGHIJKLMNOPQRSTUVWXYZ1234567

和它的逆序字符串

7654321ZYXWVUTSRQPONMLKJIHGFEDCBA

虽然写法不同，但对应同一条环形路线。

这样一来，问题的可能路线数便可以减半，只剩下32!/2种排列等待我们检验。先别急着拿笔，请注意，这个数字也就意味着我们要考察

131 565 418 466 846 765 083 609 006 080 000 000

条不同的路线。

现在，我们当然会把检验所有路线的任务都交给计算机完成。那么，让我们选一台大家伙——IBM“走鹊”（Roadrunner）超级计算机集群。它属于美国能源部，造价1.33亿美元，含有129 600个计算核心，运算速度可达每秒1457万亿次，高居2009年全球最快超级计算机五百强榜单首位²。假设检验每条路线只需要一次算术运算，那么用这台超级计算机解决含有33座城市的TSP，估计需要超过28 000亿年³，耗时漫长得可怕。要知道，宇宙从诞生至今也不过140亿年而已。难怪Menger对于TSP的暴力枚举解法并不满意。

_{2. 该榜单发布于2009年6月。但是在2012年11月的最新榜单上，Roadrunner已经退至第22位，而榜首的超级计算机Titan每秒运算速度已达到27 112万亿次。——译者注}

_{3. 原文为大约28万亿年（28 trillion），但实际计算结果应为28 600亿年（2.86 trillion）。——译者注}

上述估算简短而引人思考，但是请务必牢记，Menger只是说更快的解法尚未发现，并没有否定它们存在的可能性。John Little等人⁴在宝洁公司的赛后评论里对此总结得很到位：“有些人可能学过太多知识，所以写信告诉宝洁公司该问题不可解。这种想法是对目前科技水平的一种很有意思的误解。”在评论中，Little等人还描述了在TSP的解法研究方面取得的突破。不过计算机代码改进得不够，对于33座城市的情形还无法真正解出答案。看起来，当时似乎全美国没有一个人有能力为Toody和Muldoon设计一条路线，并确保它就是满足条件的路线中最短的一条。

_{4. Little, J. D. C., et al. 1963. Operations Research 11, 972–989.}

事实并非如此。尽管这道题确实是块难啃的骨头，但是若我们退回到1954年，就会发现，那时已经有一组人有这个能力。他们几乎一定能找到所求的最短路线，还能写出保证书一并寄去参赛。因为他们此前已经攻克了一道规模更大的类似问题，题目条件是环游美国，游览首府华盛顿和另外48座城市（分别属于当时美国的48个州）。20世纪30年代中期以来，这道难题在数学界内广为流传。《新闻周刊》报道了它的解决。⁵

_{5. Newsweek, July 26, 1954, page 74.}

图1-2　推销员之喜，《新闻周刊》，1954年7月26日第74页

给定一组城市，有一名旅行商要从指定的某座城市出发，经过其他所有城市，最终返回出发地。为他寻找最短路线的问题，并不只是一道晚饭后的智力题。数年来，它不但难倒了规划运货路线和商旅路线的商人，而且让数学家也束手无策。举个例子，假如一个推销员要拜访50座城市，那他可选的路线就有10⁶²种，这个数字是1后面连着62个0。目前的任何一台电子计算机都无法在这么多路线中理清头绪，选出最短的那条。

在美国加利福尼亚州的兰德公司，三位数学家终于提供了一种解法。线性规划方法是最近用来解决生产计划管理问题的一种新的数学方法。他们巧妙地运用了这一方法，只用了几星期时间就通过“手工”计算得到了周游华盛顿和其他48座城市的最短路线，其长度为12 345英里（约19 867千米）。他们计算使用的各城市相距里程数据取自兰德麦克纳利道路地图（Rand McNally road-map）。

这三位数学家是George Dantzig、Ray Fulkerson和Selmer Johnson。他们所在的研究中心实力雄厚，影响力极大，专门研究数学规划这一新兴学科。该中心位于加利福尼亚州圣莫尼卡市，属于兰德公司。

在他们给出的保证书里，有一些运算过程完成得很漂亮，将在本书后面的章节进行讨论。现在，最好暂时把这份保证书理解为数学证明，和我们在几何课上学过的那种证明一样。首先，Dantzig等人证明了，在这道环游美国48州问题中，周游49座城市的路线长度不可能短于12 345英里；然后，他们又提供了一条路线，其长度刚好等于12 345英里。论证与构造相结合，便彻底解决了这道题。

虽然他们没有参加那场奖金高达一万美元的广告竞赛，但是我们可以确定，按照他们的思路，用计算机解决33座城市的TSP已变得轻而易举。图1-3中画出了Toody和Muldoon的最短路线。回到1962年，尽管没有人能肯定这就是正确答案，然而确实有一些参赛者提交了这条路线，因此暂时并列第一，其中包括两位数学家Robert Karg和Gerald Thompson。他们两人发明了一种启发式试探策略⁶，从而找到了最短的路线。这个故事的结局很美好，至少对数学界来说是如此，因为决胜题要求写一篇短文赞美宝洁公司的某项产品，而Gerald Thompson凭借一篇赞颂肥皂的散文脱颖而出，最终赢得了大奖。

_{6. Karg, R. L., G. L. Thompson. 1964. Management Science 10, 225–248.}

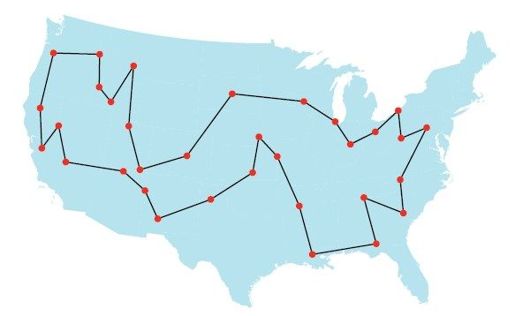
图1-3　“54号车”竞赛题的答案