6.1 割平面法

Dantzig等人得到了环游美国的路线，而他们上路的第一步就是度约束线性规划的松弛问题及其解，如图6-1所示。图中，红色的边取值为1/2，黑色的边取值为1，而其他变量取值均为0。

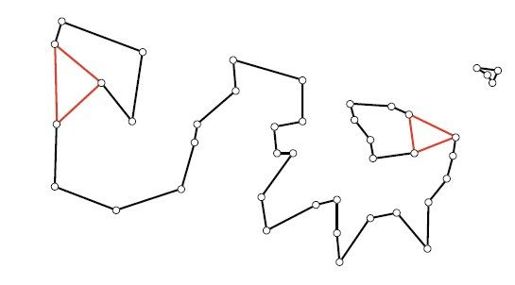
图6-1　变量取值有上界时，度约束线性规划的松弛问题的解

一看即知，单纯形算法确实没错：与每座城市相连的各条边取值之和都是2，也就是说，要么是两条黑边，要么是两条红边加一条黑边。此外，图6-1的解显然不是一条完整回路。最明显之处在东北角，那里有四座城市独立成环，孤立的子回路形成了一个孤岛，而锱铢必较的旅行商不乐意选择任何一条从孤岛通往外界的路。如果我们能够一五一十地列出所有子回路消去约束条件，那么这个问题就不复存在了。但是列出这些条件也就意味着，要向线性规划模型中加入2 199 023 254 648个不等式，这给线性规划求解程序提出了一个超级棘手的大难题。

毋庸置疑，兰德公司研究小组有优秀的人工计算能力，但是显然他们当初并没有拿到两万亿的子回路不等式直接计算，而是选择了巧妙得多的迂回解法。他们以图6-1的线性规划解为指导，着手寻找对所有路线都成立的不等式，而且不等式数目不多不少，刚好够用，从而保证单纯形算法返回的最优解就是一条完整回路。因为所有周游各城市的回路都是该线性规划模型的可能解，所以单纯形算法给出的那条回路肯定不但是最优解，也是最优回路。

下面开始解题，步骤如图6-2所示。第一步是解决东北四城市孤岛的问题，为此选择一个相应的子回路消去约束条件，如第一幅小图所示。我们把这个不等式添加到线性规划模型里之后，单纯形算法给出一个新的解，如第二幅小图所示。这时，在美国东北五大湖地区出现了另一个孤岛，由七座城市组成，于是我们再加入另一个相应的子回路不等式。单纯形算法又给出新的解，如第三幅小图所示。可是，这次的解里依然包含一个新的四城市孤岛，位于美国中部。这种做法看起来就像是修补年久失修的堤坝，东边刚刚堵上一道决口，西边立刻就出现一道新的。事实上，Dantzig等人的论文初稿里提到，研究者Edwin Paxson称该方法为“手指堵堤坝解法”¹，他是该小组在兰德公司的同事。

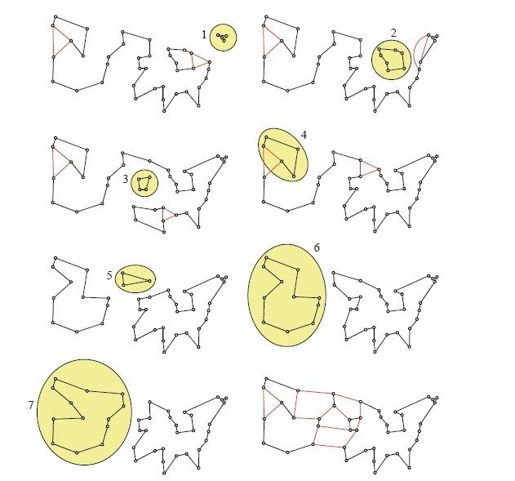
图6-2　割平面法的前七步

^{1. Dantzig, G., R. Fulkerson, S. Johnson. 1954. Technical Report P-510, RAND Corporation, Santa Monica, California. 典故出自经典儿童文学作品《银冰鞋》，作者是美国著名儿童文学作家玛丽·梅普斯·道奇。“手指堵堤坝”的故事只是书中虚构的小插曲，后来在美国家喻户晓，其主要内容是一个“勇敢”的荷兰小男孩发现堤坝有个小口子，便用手指堵了整整一夜。——译者注}

然而，外表并不是真相。诚然，他们的解法看起来可能并没有缩短与所求回路之间的距离，但是实际上确实在大步前进。按照最开始提出的线性规划模型，最优解对应的目标函数值为641，加入第一个不等式用来消去东北角的子回路之后，相应的目标函数最优值就提高到了676，而加入第二个不等式之后，更是把这个值提高到了681。最优解对应的目标函数值是最优路线长度的下界，所以虽然每次都会冒出讨厌的孤岛，但我们的方向显然没有走错。接下来的五步如图6-2所示，最优路线长度下界依次改进为682.5、686、686、688、697。

上面的最后一步给出了697的下界，而实际的最优路线长度是699，两者之差只有2个单位长度而已。胜利的曙光真是太棒了！可是要如何继续呢？长度为697的解已经不包含任何孤岛了，但是没有孤岛并不是问题所在。仔细回顾之前几步就会发现，第四步的解也是连通的，没有孤岛，当时的问题出现在西北角上，一组城市构成的团簇与外界其他城市只通过两条红色边相连，取值之和为1。再回到最后一步的解，我们并不能明显看到这样的城市集合。事实上，之后会说明，最后一步的解其实满足所有的子回路消去约束条件。这个结论很有意思，因为这意味着我们只加入了7个不等式，就计算出了满足所有子回路消去约束条件的最优解，而这些不等式的总数超过两万亿！确实是很有意思，可惜不足以解决这道42座城市的TSP题目。我们还是得想法设法把下界提高到最优路线的长度才行，也就是要从697提高到699。

好吧，所有子回路消去约束条件统统没用了。没关系，在描述这道题目的TSP多面体中，还有好多好多别的不等式可以选择呢。我们只需要找到上面的解不满足哪一个就行了。Dantzig等人当时借助富有新意的专门论证，明确描述了两个合适的不等式。我们可以不必使用专门论证，而是给出一条一般性的规则。这条规则讨论的是所给城市的4个子集，它们之间的关系如图6-3中左图的文氏图所示。自己试着连出几条回路，比如右图展示的那一条，你就会明白，每条回路穿过4个集合边界的次数必然是至少10次。换言之，把这4个集合对应的子回路不等式加起来，再把不等式右端换成10，则每条回路都必须满足这个新的约束条件。¹

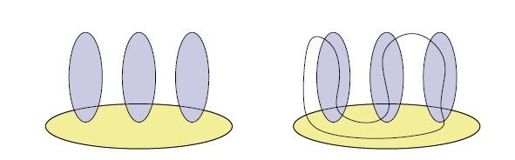
图6-3　四集合结构，此时回路穿过集合边界的次数必然是至少10次

^{2. 请注意，满足子回路不等式取值为2的回路只有一种情况，就是进入该子集，到达其中每座城市，然后离开该子集。因此，在该子集内部，这条路线相当于一条简单通路。如果图中3个蓝色集合都有这么一条通路，那么黄色集合就必须与路线相交至少3次。但是一条路线与任一集合边界都必然相交偶数次，也就是说黄色集合与路线必须相交至少4次。综上所述，路线与3个集合各相交2次，与1个集合相交4次，因此相交的总次数至少为10。}

有了上述的四集合结构，环游美国问题的最后几步也可以完成了，如图6-4所示。第一幅图标出了4个集合，它们对应的不等式就是第8个约束条件。黄色集合边界共被3条黑边穿过，其中1个蓝色集合边界由4条红边穿过，另外2个蓝色集合边界则都由2条红边和1条黑边穿过。把这些数目加起来可知，穿过这4个集合全体边界的黑边总数是5条，红边总数是8条，在线性规划模型中，取值之和为9。³之前我们要求这个数值应该至少为10，所以这就是我们要找的不等式。把相应的四集合不等式添加到现有的线性规划模型中，重新求解，得到的最优解取值为698，如图6-4的第二幅小图所示。再加入另一个四集合不等式，终于大功告成了：单纯形算法给出了一条新路线。现在，借助对偶线性规划问题的解，我们可以让所有人相信，699确确实实是这道TSP例题的最优值。

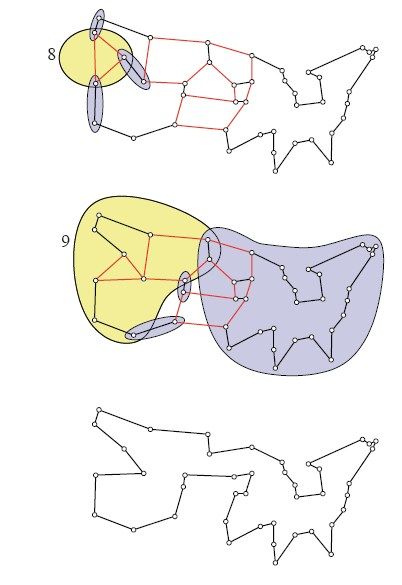
图6-4　割平面法的第八步和第九步

^{3. 注意在红边三角形中，每条红边都分别穿过两条边界，因此计算总数时就要数两次。}

我们总共用了9个不等式，解决了旅行商周游美国的路线难题。所有不等式共有两万亿个，实际解题时却只用到了9个，这真是太神奇了！兰德公司研究小组慧眼如炬，居然敢于尝试这样的逐步求解过程。你如果能意识到所需手工计算的工作量有多大，肯定会为他们的远见卓识所折服。

最终选出的9个不等式称为割平面（cutting plane），因为每一步，对应的半空间（也就是半平面）都把线性规划模型的可行域一割两半，使当前的解落在切掉的那一块里。“割平面法”这个名字不像Paxson提议的“手指堵堤坝解法”那样引经据典、辞藻华丽，但是也没有那么悲观绝望。

在那篇著名论文的结尾处，Dantzig等人谦逊地写下了下面这段结语。⁴

^{4. Dantzig et al. (1954).}

显然，对于人们可能提出的理论本质与旅行商问题相关的任何题目，我们几乎都没有给出解答。但是，我们希望本文已经有效地展示出了，包含的点不多的题目是可以得到解决的，也希望这里用到的部分思想同样能够用在具有类似本质的其他问题上。

确实很有效！他们的研究工作影响深远，余韵至今仍然在应用数学界回荡不息。