8.1 世界纪录
说到TSP世界纪录,毫无疑问必须把Dantzig、Fulkerson和Johnson的研究列在首位。
对这么大规模的TSP题目,三位作者都能够通过手工计算找到最优解并证明其最优性,实在是太惊人了。
——George Nemhauser和Martin Grötschel,2008年1
1. Grötschel, M., G. L. Nemhauser. 2008. Discrete Optim. 5, 168-173.
Dantzig、Fulkerson和Johnson展示了求解大型TSP题目的一种方法,后面的解法都只是锦上添花而已。
——David Applegate等人,1995年2
2. Applegate, D., et al. 1995. DIMACS Technical Report 95-05. DIMACS, Rutgers University.
后来,世人终于领会了兰德小组的研究工作,把他们的技术推广到不同的应用方向,得到了其他重要成果。但是若论创新思想之丰富,影响作用之广泛,系统阐述之水平,他们发表于1954年的原始论文始终是旅行商问题研究史上最伟大的成就。
8.1.1 随机选取的64个地点
紧接Dantzig等人的工作之后,TSP研究前线风平浪静了好几年。虽然人们尝试了五花八门的方法,可是计算测试的题目一般仅限于10座城市上下的规模。到了1971年,Michael Held和Richard Karp终于迈出一大步,开始推进规模更大、难度更高的计算,给这段枯竭的岁月画上了句号。1
1. Held, M., R. M. Karp. 1971. Math. Program. 1, 6-25.
在1985年的图灵奖获奖演说(Turing Award Lecture)中,Karp明确陈述了Held-Karp研究的用意。“数年前,兰德公司的George Dantzig、Raymond Fulkerson和Selmer Johnson,结合人工计算和自动计算,曾成功解决一道49座城市的问题。而我们希望打破他们的纪录。”2
2. Karp (1986).
他们确实打破了纪录。Held和Karp先是再次解决了同一道49座城市的题目,接着继续解决了一道环游美国57座城市的题目,又攻克了一道64座随机城市(采用直线距离)的题目。获胜法宝是基于复杂定界机制的算法和程序。定界机制源自生成树,得到的界则整合到分支定界搜索过程中。该方法用在测试题目上,能产生非常小的搜索树。3
3. Interview with Richard Karp, October 24, 2009.
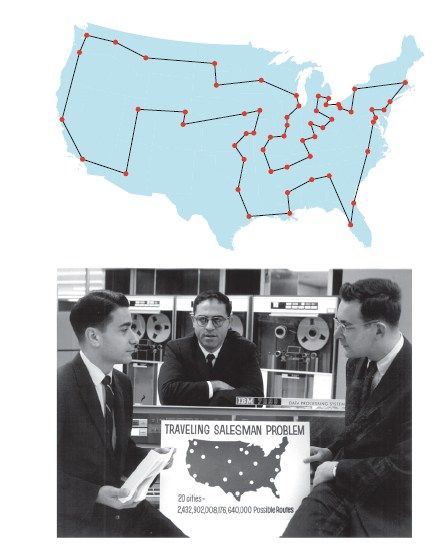
图8-1 上图:包含57座城市的Held-Karp最优路线;下图:Michael Held、Richard Shareshian和Richard Karp,1964年。IBM Corporate Archives提供图片及照片
真是振奋人心的结果。此前我们历尽艰难险阻,如今突然如有神助。分支定界过程中,生成的树往往相当狭小,偏差很少,给出的界限也非常好,几乎直接就能得到最终解。
在所有创纪录的TSP计算中,Held-Karp研究是独一无二的,因为它并没有直接利用割平面法。不过,他们用到的定界机制确实与线性规划及Dantzig等人的成果有联系。事实上,子回路线性规划的松弛问题中,目标函数的最优值可由Held-Karp法的界给出近似。而且,该方法的全过程可以视为绕开一般线性规划解题软件的做法。他们避免使用线性规划解题程序,并不能反映出当时此类程序质量如何,只是运行割平面法必须要迭代求解,而当年可用的软件确实很难如此使用。
8.1.2 随机选取的80个地点
后来,几个研究小组对Held-Karp的分支定界法作了局部细节修正。1975年,意大利的一个研究团队成功借此解出了一道采用直线距离的题目,规模提高到了67座城市。1但是,割平面法注定要卷土重来,毕竟除了子回路消去约束以外还有其他不等式,它们的力量非常强大,可以大大提升Held-Karp法得到的界。
1. Camerini, P. M., et al. 1975. Math. Program. Study 3, 26-34.
在Ailsa Land的领导下,伦敦政治经济学院的研究小组实现了反击。她的学生Panagiotis Miliotis结合割平面法和一般的整数规划,解决了一系列随机选取地点的题目,测试题目采用直线距离,最多可达80座城市。这种综合解题方法最早是由Glenn Martin在20世纪60年代中期提出的。2求解过程大致如下。首先,从度约束线性规划的松弛出发,限定所有变量取值只能为0或1,应用Gomory的整数规划割平面算法。如果得到的解是条完整回路,则它必定是最优解;否则,找出已知解违背的若干个子回路消去约束条件,加入模型中,重新调用Gomory算法,重复该过程。
2. Miliotis, P. 1978. Math. Program. 15, 177-188.

图8-2 Panagiotis Miliotis,1974年
Miliotis求解80座城市的题目时,所需的总运行时间只有不到一分钟。这意味着即使题目规模更大,也能够解决。然而,Miliotis却说出了下面的评语。
不幸的是,利用割平面的过程需要占用A矩阵(约束条件系数矩阵)大量空间。一道随机选取90座城市并采用直线距离的题目没能获得解决,这是正常的,因为A矩阵中非零元素的数目超过了30 000,而这些元素大部分都出现在割平面约束条件里。
Gomory法的这一特性实在令人扼腕,每加入一个割平面,约束条件里都包括线性规划模型的几乎所有变量,最终会严重拖慢单纯形算法的速度,以至于无法取得进展。相比之下,Dantzig等人的方法简单而又美好,其中的TSP不等式往往会把多数边赋值为0,产生的线性规划模型依然比较容易解出答案。
8.1.3 德国的120座城市
下一个TSP纪录的创造者是Martin Grötschel。他的方法是纯粹的割平面法:他求解模型使用了线性规划解题软件,但寻找不等式只用了手工计算,颇得1954年兰德小组研究的真传。我们已经在第1章见过他的成果,图1-9的三条周游德国的路线里,经过120座城市的那一条就是他的最优路线。

图8-3 Martin Grötschel,2008年,照片由德国柏林祖斯研究院提供
在计算这条破纪录的路线的过程中,Grötschel解决了13道线性规划的松弛,总共用到了36个子回路消去约束和60个梳子不等式。每道线性规划的松弛都给出一个界,手工计算用时在30分钟到3小时之间,而换成计算机时间则相当于30秒钟到2分钟之间。1他使用的线性规划解题工具是IBM的MPSX套装软件。在2005年6月11日的一封电子邮件里,他如下描述了计算的全过程:
1. Grötschel, M. 1980. Math. Program. Study 12, 61-77.
MPSX运行一次之后,我把解打印出来,画出对应的路线图。然后我复制几分副本,想办法寻找割平面。当然,积累一定经验以后,我能找到路线违背的好多不等式。但是,当年MPSX无法解决规模很大的线性规划问题,所以我只能精心选择看上去效果不错的割平面,把数目限制在每次运行只加入5到20个的样子。
这是一项非凡的成就,展示出了梳子不等式用来求解大型TSP题目的强大威力。
8.1.4 电路板上的318个孔洞
Grötschel计算完120座城市的题目之后,没过多久,Manfred Padberg立即启动了一项联合研究。他的合作者是Saman Hong,刚刚从美国约翰霍普金斯大学毕业的博士生。他们的项目是将割平面算法自动化,取得了计算方面的成功,不但能解决多达75座城市的题目,而且在其他题目上可以计算出很好的下界。1该研究中,规模最大的例题是一道318座城市的钻孔题目,此前由Shen Lin和Brain Kernighan考查过。
1. Padberg, M. W., S. Hong. 1980. Math. Program. Study 12, 78-107.
Padberg不满足于取得好的近似结果,而是在几年后继续探索上述Lin-Kernighan例题的解。这一次,他的合作者是IBM公司的Harlan Crowder。2
2. Padberg, M. 2007. Ann. Oper. Res. 14, 147-156.
有天晚上,我们把一切都准备好,让计算机运行一次,求解那道318座城市的对称TSP。我们估计得花好几个小时,于是就去了“侧门”餐馆吃饭,它距离IBM研究中心不远。吃完饭回来的路上,我们讨论了万一程序失败,可以新加入哪些“花里胡哨”的玩意儿。到了IBM研究中心,我们去计算机房看有没有完成输出,结果发现有。程序明确表示,它在不到6分钟的计算机时间内,找到了最优解!
这道318座城市的题目以及许多规模较小的题目之解,为Crowder-Padberg研究画上了圆满的句号。3
3. Crowder, H., M. W. Padberg. 1980. Management Science. 26, 495-509.

图8-4 左图:318座城市的钻孔问题的最优解;右图:Manfred Padberg(右二)和Harlan Crowder(前排坐者),1982年(照片由Manfred Padberg提供)
8.1.5 全世界的666个地点
下面,我们来到1987年。TSP计算研究再次掀起高潮,只有1954年的“大爆炸”可以与之相提并论。那一年公布了两项重大研究,第一项是Martin Grötschel和Olaf Holland攻克了大量测试题目,最难的一道包括从世界各地选取的666座城市。看到数字666,《圣经》研究者会说它是“兽的数目”1。实际上,Grötschel选择这些城市时,确实有意创造出一道有如洪水猛兽般的TSP计算难题。2Grötschel和Holland结合使用了割平面法与一般整数规划,解决了这道难题。这一次,他们的整数规划求解程序是IBM的MPSX-MIP/370程序。他们之所以能获得计算上的成功,主要归功于新发现了许多启发式准确分离算法,可以用于梳子不等式,从而使程序得到非常强的线性规划松弛解。
1. 出自《圣经·启示录》3-18。——译者注
2. Grötschel, M., O. Holland. 1991. Math. Program. 51, 141-202.
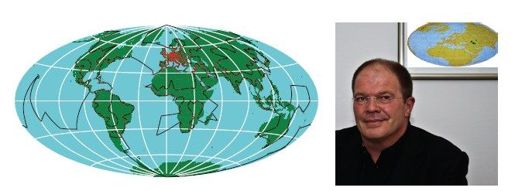
图8-5 Grötschel-Holland周游666座城市的路线(左);Olaf Holland(右),2010年
8.1.6 电路板上的2392个孔洞
无论是Glen Martin还是Panagiotis Miliotis,抑或是Grötschel和Holland,都综合使用了不止一种方法,用到了高效的整数规划解题程序。但是1987年的第二项重要研究却与众不同。Manfred Padberg和Giovanni Rinaldi的研究清晰地表明,完全把求解过程限制在TSP领域内也有诸多好处。他们使用的工具是分支定界法。他们的计算机程序解决了许多测试实例,包括周游美国532座城市的题目,前面提到的666座城市的Grötschel-Holland难题,还有分别包含1002座城市和2392座城市的钻孔问题。最后这道2392座城市的TSP题目宣告解决,意味着他们取得了一项惊天动地的成就,而且其计算显然也是截至当时最复杂的最优化问题解答过程。1
1. Padberg, M., G. Rinaldi. 1991. SIAM Review 33, 60-100.
Padberg-Rinaldi的研究引人注目,借助了大型的计算硬件,其中就有美国国家标准局的一台CDC Cyber 205超级计算机,还有IBM公司纽约沃森研究中心的IBM 3090/600矢量计算机。但是改进TSP结果的动力其实是算法方面的工作,包括用于梳子和团树的新型启发式分离算法,以及分支切割法程序实现的众多新方法。他们在论文的最后给出了乐观的注记:“在对称型旅行商的长篇传奇故事里,2392座城市的题目不会是最终结局。”

图8-6 上图:2392个孔洞的印制电路板的最优路线;下图:Manfred Padberg和Giovanni Rinaldi,1985年(Manfred Padberg供图)
8.1.7 电路板上的3038个孔洞
我和Dave Applegate、Bob Bixby、Vašek Chvátal在1988年开始合作研究,希望能续写传奇。最初,我们坚持不做别人做过的事情,试图避免使用割平面法。但是没过多久,我们就意识到自己犯了大错。到了1989年,我们已经埋头于分支切割法的具体工作中。我们的第一版程序名为“Subtour”(子回路),因为编写它的初衷只是为了计算子回路线性规划的松弛之最优解,用来衡量不使用割平面法获得的界是好是差。后来,程序渐渐扩充增强,加入了一组新的分离例程,还用上了之前介绍过的强分支算法。
我们的计算研究基地是贝尔通信研究实验室(Bellcore),位于美国新泽西州。这里容纳有大约50台桌面工作站,当这些计算机的主人不在办公室时,我们就可以加以利用。每一台机器与Grötschel-Holland和Padberg-Rinaldi研究中用到的大型机相比,都完全不可同日而语,但是几十台构成网络联合起来,就有了惊人的速度。因此,把寻找割平面和处理子问题的任务分而治之,建立起一种并行处理方法,就是自然而然的事了。
不幸的是,觊觎空闲免费机时的并不只是我们这一群人。Arjen Lenstra是我们的对手,他领导了129位的数字RSA129的素因数分解工作1。争抢机时的过程不是彻头彻尾的友好竞争,不过最终双方团队都分到了为数不少的可用硬件。我们的策略简单明了:只在当前空闲的计算机上启动我们的软件,唯一例外是允许Lenstra同时运行他那烦人的分解因数程序,而且只要嗅探到机主回到工位上,就立刻终止程序。Dave Applegate编写了一小段程序,每秒检查几次是否存在用户输入,比如鼠标移动或者键盘敲击,从而实现了这种策略,而且让真正的机主极难发觉我们的手脚,他根本不知道我们接管了他的机器:如果他敲一条指令来看看机器在运行什么,那么指令的结果还没来得及发送到屏幕上,我们的程序就已经消失得无影无踪了。
1. RSA因数分解挑战(RSA Factoring Challenge)涉及的整数都是信息安全公司RSA(已被美国EMC公司收购)认为难以分解成素因数之积的数。RSA公司提供奖金,分别悬赏成功分解各数的人。
使用贝尔通信研究中心的上述网络,我们在1992年迎来了第一项成果,解决了一道3038座城市的电路板钻孔问题,题目出自Gerd Reinelt的TSPLIB题库。然后,我们在程序和算法中加入各种细微改进,在1993年得到一条周游旧时东德4461座城市的路线,又在1994年攻克一道7397座城市的计算机电路题目,先后刷新自己的结果。此时,我们达成一致,决定中止TSP项目,但是收尾过程并没有按照计划圆满完成。这或许是我们的幸事。

图8-7 左图:David Applegate;右图:Robert Bixby,由Jakob Schelbert拍摄,德国埃尔朗根,2010年
8.1.8 美国的13 509座城市
我们决定结束计算后,开始着手回顾多至7397座城市的TSP题目,整理记录其中用到的技术方法。这时,我们遇到了麻烦。既然我们自己都对研究细节不满意,想要说服其他研究者相信我们确立了可靠的解法,谈何容易!随着我们发现新的技巧,子回路Subtour程序也跟着时不时改进,但它不能体现出我们对于TSP计算的全局观点。有鉴于此,我们作出了唯一的理智选择——放弃。我们没有整理旧程序的文档,而是从零开始编写全新的程序,并称之为Concorde。
整个项目推倒重来非常难得,我们抓住这次机会,把针对规模大得多的TSP题目的算法和技术都整合进来。新增内容中,有一个“局部切割”分离例程非常关键,它依靠城市簇收缩来获得非常小的图,如此一来,某种基于线性规划的割平面搜索方法虽然耗时很长,也可以派上用场。
我们的计算研究主要意在解决一道13 509座城市的周游美国路线,并于1998年获得成功。此后的数年内,我们继续进行研究,但是主要目标则是理解消化已有的内容,就好比是赛车手逐渐熟悉新车一样。在此期间,我们于2001年计算出了周游德国15 112座城市的最优路线,并于2004年计算出了环游瑞典24 979座城市的最优路线。
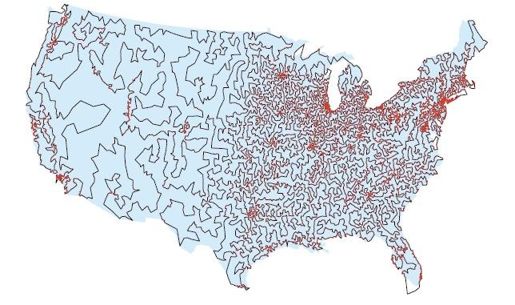
图8-8 周游美国13 509座人口不少于500人的城市的路线
8.1.9 计算机芯片上的85 900个门电路
那道瑞典之旅题目的TSP计算,将Concorde的能力推向了极致。这项作业是在佐治亚理工学院完成的,用到了96台双处理器计算机构成的集群。程序作为后台进程,在机器没有其他活动时运行。总的计算机时间长达84.8年。
周游瑞典的路线颇令我们洋洋自得,但是TSPLIB里还有两道更大的题目,分别包含33 810座城市和85 900座城市,它们似乎超出了Concorde程序的能力范围。好在正当此时,Daniel Espinoza和Marcos Goycoolea对Letchford分离算法的程序实现出现在了网上(见6.3节最后的讨论部分),为我们带来了足够的马力,足以一试身手,挑战一下能否彻底解决Reinelt的TSPLIB题库里的所有题目。

图8-9 Daniel Espinoza(左)和Marcos Goycoolea(右)
2005年2月,我们开始对85 900座城市的TSP题目展开最后一轮程序运行。2006年4月,最优解诞生,宣告计算结束。线性规划的界稳步攀升,如图8-10所示,其中数据点取自几乎每天都有的计算日志,唯一的中断是2005年12月,当时恰逢计算机集群统一安排维修。终于有一天,计算出来的下界比当时已知的最好路线的长度只差不到0.001%了,那条路线是由Keld Helsgaun于2004年发现的。0.001%的差距已经足够接近了,使用分支切割法只需稍作搜索便能很快完成剩下的这一点工作,证明Helsgaun的路线就是真正的最优路线。
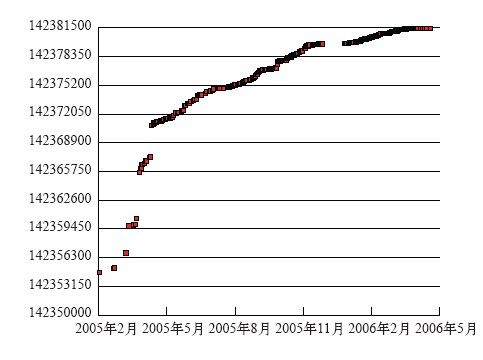
图8-10 85 900座城市的TSP题目计算中,线性规划的界不断改进
虽然我们自己声明已经解决了这道题目,但是计算耗费了136年的计算机时间才完成,所以其他人当然都很难确切核实真相。因此,2009年,我们公布了一则计算机程序和数据集,保证了85 900座城市的路线的最优性1,与它的创纪录地位相一致。分支切割搜索步骤中,每一道子问题对应的割平面和对偶线性规划之解,都在公开数据之列。而计算机程序比较精致,包括6646行C语言代码,能够遍历所有子问题,证明对偶线性规划问题之解可以给出界并用来逐个舍弃子问题。这样的证明不如毕达哥拉斯定理2的证明那么简洁,但是确实为未来的TSP研究者留下了充足、丰富的信息,让后来者能够追根究底,真正理解这场大规模计算的成果。
1. Applegate, D. L., et al. 2009. Op. Res. Let. 37, 11-15.
2. 又称勾股定理。——译者注
