8.2 规模宏大的TSP

TSP的计算之美在于一个简单的事实：题目规模没有最大，只有更大。

8.2.1 Bosch的艺术收藏品

告别TSPLIB测试题集，就轮到Bob Bosch的挑战题目登场。我非常喜欢他创造的这些难题，编写题目所用的技术将在第11章介绍。他的六道题目规模各异，最小的是100 000座城市的“蒙娜丽莎”TSP，最大的则是200 000座城市的维米尔名画《带珍珠耳环的少女》“摹本”。数据集公开在网络上，任何人如果有意寻找更好的路线，或者确定路线长度的下界，都可以自由获取。¹

^{1. 参见http://www.tsp.gatech.edu/data/art/index.html。}

Bosch测试问题中，“蒙娜丽莎”TSP迄今吸引的注意力最多，毕竟它只比85 900座城市的求解纪录高出一丁点儿，难免让人心痒手痒。可是，85 900座城市和100 000座城市之间差别虽小，或许却是障眼法。无论怎么看，“蒙娜丽莎”TSP都很可能比当前的世界纪录要难得多。实际上，后一道计算机电路实例如图1-8所示，可以看到，其实有许多城市紧密排成直线。这种几何性质表明，那道85 900座城市的题目也许外强中干，规模大但难度却相对较低。再看看“蒙娜丽莎”TSP的各点分布，简直是要多复杂就有多复杂。

第1章已经提过，永田裕一在2009年3月17日发现了“蒙娜丽莎”TSP的当前最好路线，谁能找到更短的路线，就能获得1000美元的奖金。2009年2月和3月，Bosch刚刚创建完成数据集，全世界最优秀的路线寻找专家纷纷活跃起来，永田裕一的计算结果将竞争推向高潮。在此期间，最好路线的纪录六易其手，他凭借长度为5 757 191的路线拔得头筹，这比前一天由Keld Helsgaun发现的路线短了8个单位长度。但是这就是最优路线吗？

2010年1月18日，5 757 044确定为“蒙娜丽莎”TSP路线的下界。至此，下界与永田裕一路线之间仅仅相差147个单位长度。看上去近在咫尺，只有0.0026%而已，可是差距依然存在。新的下界是由Concorde分支切割搜索得到的，总共历经1065个子问题，耗时66天，换算成计算机时间则长达4.37年。也许继续运行几轮Concorde程序，有机会再缩减几个单位长度的差距。但是要想真正填补缺口得出结论，大概必然需要新的思想，尤其是割平面分离的新思路。对我这种计算狂人来说，现在好戏才刚刚开始呢。

8.2.2 世界

世界旅行商问题有1 904 711座城市，正在等待有识之士前来做出TSP计算的一流突破。它的数据取自美国国家图像与测绘局（National Imagery and Mapping Agency）和美国地质调查局（Geographic Names Information System）数据库。该题于2001年问世，覆盖了当时全球各地人类居住的每一处。这些位置由经度和纬度指定，旅行成本则是把地球视为球体，用两点间的大圆劣弧长度近似给定。如此定义的成本函数是由TSPLIB里的GEO标准稍加变化而得到的，GEO标准以千米为单位，而这里则换算为米作单位。

图8-11　周游世界所有城市的路线，图片由David Applegate提供

2001年秋季，研究者根据一条长度为7 539 742 312米的初始路线，以及数值为7 504 218 236的路线下界，确定两者之间有0.47%的最优性差距（optimality gap）。从那时起的10年间，新的计算结果不断地“蚕食”上述差距，路线改进方面主要归功于Keld Helsgaun，而下界加强方面则基本归功于Concorde程序。最优性差距不断缩小，如图8-12的柱状图所示，其中下界加强带来的改进用红色条块表示，路线优化带来的改进则用灰色条块表示。当前的最好路线是Helsguan提出的，长度为7 515 790 345，最强的线性规划下界则是Concorde程序给出的7 512 218 268，由此可得，差距为0.0476%。

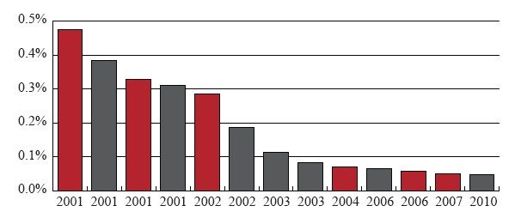
图8-12　世界旅行商问题的最优性差距逐年递减

过去10年间，最优性差距不断压缩，如今只有原始值的1/10强，可谓进步显著。有趣的是，其中近乎75%的改进都是由路线优化获得的。在2001年的TSP世界，谁也没有预料到上述事实。当时人们普遍认为，TSP启发式算法是尖端技术，能给出近优解，所以肯定是线性规划下界太弱才导致了一开始的最优性差距。Helsgaun的LKH程序表明，寻找路线的方法还有改进空间，从而改变了传统的观点。此时此刻，我无法猜出最优值究竟位于何处，不知道它究竟是距离路线长度7 515 796 609更近，还是距离下界7 512 218 268更近。

尽管如此，对Concorde程序加以工程改进，肯定能够提升线性规划的界。比如，目前由于数据集规模太大，无法在程序中使用多米诺奇偶性分离模块。但这其实是个好消息，说明我们又有活儿可干了！

8.2.3 恒星

2003年，我和Dave Applegate设计了一道TSP题目，囊括了美国海军天文台USNO-A2.0星表（United States Naval Observatory A2.0 catalog）里记录的全部天体，共计有526 280 881个之多。至少在可以预见的未来，这或许就是TSP计算的终点站。我们最初想要收入每对天体之间的距离估计值，如果能让“进取号”（Enterprise）在下一个五年任务里沿着最优路线前进，将会很有意思。¹但是遗憾的是，数据太粗糙了，会导致所有恒星都落在为数不多的几个同心球面上。因此，我们决定改为模拟望远镜的移动方式。这样一来，数据就把TSP城市指定为天空中的位置，任意一对城市之间的旅行成本便可由两点确定的夹角度数给定。

^{1. “进取号”是著名科幻系列作品《星际迷航》（又译《星际旅行》）中的星际舰船，它所肩负的五年任务是探索新世界，寻找新生命及新文明，驶向前人未至之境。——译者注}

整体处理恒星旅行商问题非常困难。当n取值高达5亿时，即使是n²复杂度的运行时间也太漫长了。故而，目前的目标就是发展拆分数据集的方法，确定各部分的界和路线，然后再把它们拼到一起。按照这种方法，我和Dave Applegate、Keld Helsgaun、Andre Rohe做了初步的试验，并于2007年获得了0.41%的最优性差距。这意味着，恒星旅行商问题的状态落后于世界旅行商问题，相差大约10年的光景。所以，如果你对路线或者界限有什么奇思妙想，请记得用在这个大规模数据集上。

图8-13　星图（由美国宇航局戈达德太空飞行中心科学可视化工作室提供）