1.3 循序渐进，各个击破

将来或许会有人一举攻破终极的复杂性问题，给出惊天动地的答案。在那之前，我们能做什么？直面旅行商问题，目标非常明确：求解更大规模、更难解决的情形。

TSP是算法工程（algorithm engineering）¹的代表问题。这门研究学科重视实用性，以不达目的誓不罢休为理念。理论上，TSP的规模一旦大到一定程度，求解某些实例的计算量就可能高得离谱。但这并不代表只要看到规模很大的具体问题，就只能退而求其次，选择粗略估计作为结果。研究人员正是在这种绝不妥协的态度的推动下，不断改进计算机代码和技术方法，如今已能解决复杂度惊人的大问题。

_{1. “算法工程”这个名词至少可以追溯到1997年，当年在意大利威尼斯举行了首届算法工程研讨会。一个课题组得到了德国科学基金会的资助，致力于算法工程的研究，并把这门学科的内容描述为“实用算法的设计、分析、实现与实验评估”。Petra Mutzel是课题领导者之一，同时也是多特蒙德大学的算法工程学教授。}

在TSP研究领域，如果有人攻克了一道未解难题，消息会迅速流传开来，就像登顶喜马拉雅山脉某座处女峰或者打破百米短跑的纪录一样轰动。这并不是因为我们迫切渴望知道这道题目答案的具体细节，而是因为我们迫切需要知道TSP的研究能够继续推进，哪怕只是一小步。也许最终我们注定会败在旅行商手下，但是至少我们曾经拼搏过。

1.3.1 从49到85 900

兰德公司的Dantzig、Fulkerson和Johnson是TSP领域的三位英雄人物。虽然计算机时代已经拉开序幕，持续出现大批新人参与研究，但是Dantzig等人通过手工计算得到的49座城市的纪录始终无人能及。算法推陈出新，计算机代码反复编写，研究报告不断发表，然而年复一年，他们的纪录依然屹立不倒。终于，IBM研究员Michael Held和Richard Karp打破了Dantzig等人的垄断局面。Karp正是我们之前提到过的那位计算机科学家。他研究过TSP无法解决的可能性，但是显然并不满足于空谈理论。他们测试的范例是正方形区域内随机分布的64个点，以每两点之间的直线距离代表旅行费用。

接下来的好几年里，尽管有些研究小组对算法稍加改进，试图挤出一点提升的空间，但没有人能打破Held和Karp的绝对领先地位。直到1975年，由Dantzig等人提出的方法重出江湖。这次，Panagiotis Miliotis对他们的想法做了一些改动，并计算出经过80个随机点的最短路线，使Held和Karp的纪录黯然失色。

图1-6　TSP的新纪录，包含3038座城市，《发现》（Discover）杂志，1993年1月

由Miliotis的研究看来，Dantzig等人的方法可能具有极大的威力，远远超出人们对TSP计算极限的预期。此后不久，Martin Grötschel和Manfred Padberg所做的理论研究进一步证实了这一点。这两位数学家在TSP的舞台上叱咤风云长达15年之久，为TSP基本方法的重大推广奠定了基础。他们的成功始于1977年，当时Grötschel在博士论文中构造了周游德国120座城市的路线。随后，Padberg和IBM研究员Harlan Crowder合作，解决了一道出自电路板钻孔问题的实例，对318座城市的情形算出了结果。

尽管这两个结果本身都非常出色，但是直到1987年他们陆续宣布一系列惊人发现的时候，人们才发现，原来之前只是牛刀小试而已。1987年是TSP历史上的丰收年。Grötschel和Padberg两人的研究小组分别在大西洋两岸独立展开研究，很快解决了一道又一道实例：周游美国532座城市，环游世界666个地点，分别含有1002座城市和2392座城市的电路板钻孔问题……Grötschel当时在德国波恩大学和博士生Olaf Holland合作研究，而Padberg则在美国纽约大学与意大利数学家Giovanni Rinaldi共事。

1988年初，乘着这股热潮，Vašek Chvátal和我也决定加入TSP计算的竞争中。前面有Grötschel和Holland、Padberg和Rinaldi的杰出工作，奋起直追的我们没有丝毫优势。不过我们很幸运，因为同时期有那么多来自世界各地的研究人员，他们非常活跃，对该问题的理论方面开展了前所未有的深入钻研。我们仅仅通过筛一遍日益增加的相关研究，就能获取可以用来解决计算问题的强大工具。不过，在正式动手之前，我们迈出了所有工作中最重要的一步——招收David Applegate和Robert Bixby为小组成员，他们两位是当代实力最强的计算数学家。研究起初进度缓慢，好几次走错了方向。1992年，我们成功利用计算机网络并行计算，解决了一道来自电路板钻孔的问题，其规模为3038座城市，创下当时纪录。此时，方法已经成形。在此基础上，我们又在1998年计算得出了周游美国13 509座城市的最优路线，于2004年得到了周游瑞典24 978座城市的最优路线，最终在2006年解决了一道来自实际应用的问题，其规模达到85 900座城市。我们使用的计算机代码名为“Concorde”¹，网上到处都可以找得到。

_{1. Concorde代码是用C语言编写的，源代码和程序都公开提供下载。读者如果想深入学习，可以访问http://www.tsp.gatech.edu/concorde/index.html获得相关资源。——译者注}

在最后一道创纪录的问题里，85 900座城市代表的是一枚计算机芯片上的不同位点。为了加工定制芯片，需要用激光切割这些位点，而激光光头在各点之间的移动顺序便可转化为TSP模型。尽管每次移动距离只是毫米量级，但总移动时间对芯片生产成本的影响却很大。图1-7和图1-8分别是激光移动的最优路线图和路线局部放大图。

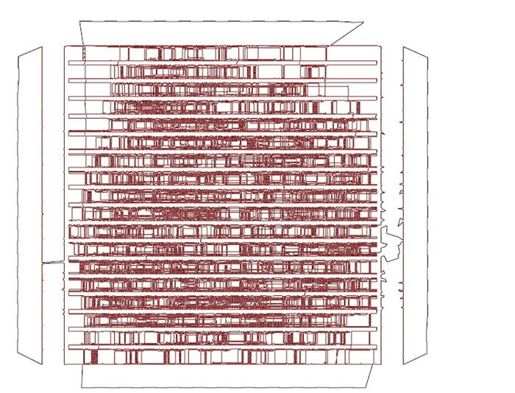
图1-7　包含85 900座城市的TSP路线，题目出自计算机芯片应用

图1-8　包含85 900座城市的TSP路线局部放大图

1.3.2 世界旅行商问题

在包含85 900座城市的芯片问题和其他一些电路板钻孔的应用实例中，各点都具有类似网格点的分布形式。早年环游美国48州的题目开启了TSP的漫长研究，而这些例子显然没有真正体现当初那种旅行的精神。不过，仔细观察图1-9所示的三条周游德国的路线，还是很容易体会到，现代的结果在复杂度上的确有所提高。图中规模最小的路线经过33座城市，简称为《指南手册》路线，出自1832年的一本旅行商指南小册子。蓝色路线经过120座城市，是当年Grötschel破纪录的成果。背景里的那条路线则是2001年由Concorde代码对15 112座城市计算得到的最优路线。

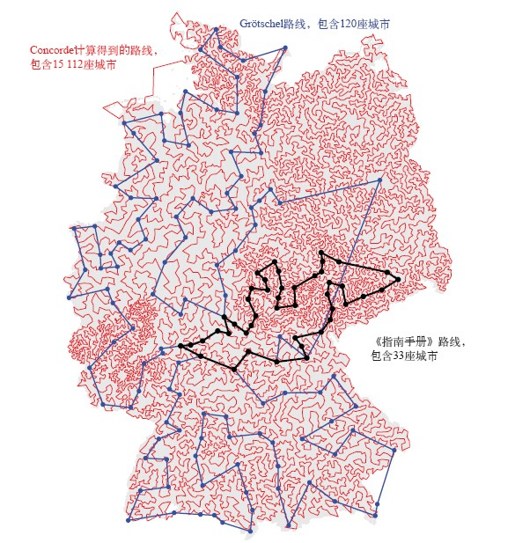
图1-9　周游德国的三条路线

也许对德国之旅来说，这条包含15 112座城市的路线就是最完满的路线了。但如果我们将世界上所有城市、区县、乡镇都囊括在内，就连南极的几处科考基地也算上，构造出一个总共包含1 904 711座“城市”的终极旅行挑战，这条路线便远远不够了。这道世界旅行商问题诞生于2001年。来自世界各地的计算机代码纷纷在它面前败下阵来，Concorde也不例外。如果克雷数学研究所的百万悬赏不合你胃口，或许这道世界级难题能点燃你的斗志。截至本书出版之时，本题最著名的路线是由丹麦计算机科学家Keld Helsgaun于2010年10月10日发现的，长度为7 515 790 345米。我们几乎可以肯定，这并非最好的结果，但也已由Concorde计算得知，不存在长度短于7 512 218 268米的路线。这样一来，Helsgaun给出的解最多只比真正的最短路线长0.0476%。两者已经很接近，不过依然有充足的余地让我们再抄几条近道。

1.3.3 《蒙娜丽莎》一笔画

为上面那道世界旅行商问题找到最优路线将是了不起的成就，但是求解需要用到的工具方法很可能要在10年以后才会出现。幸好，在征服世界的途中，从来不缺有趣的问题。一个漂亮的例子就是如图1-10所示的《蒙娜丽莎》TSP，总共包含100 000座城市。

图1-10　根据列奥纳多·达·芬奇的画作《蒙娜丽莎》设计的TSP，路线由永田裕一发现

Robert Bosch于2009年2月提出了这道题目的数据集，希望用一条连续曲线画成达·芬奇的这幅名画。日本北陆先端科学技术大学院大学（JAIST）的永田裕一（Yuichi Nagata）取得了迄今为止最好的结果。他的路线最多只比最优路线长0.003%。差距如此之小，令人迫不及待，但毕竟还没有真正完成。有一项1000美元的奖金将颁发给第一个突破永田裕一结果的人，以激励有意参与这道题目的研究者。奖金不错，但是请你铭记在心：问题挑战之所以一道接一道，真正的目的在于积累思路，以便在TSP的通用解法研究以及更大范围的应用领域派上用场。解决问题的新途径才是关键所在。