6.2 TSP不等式一览

Dantzig等人在解题过程中用到了两个非子回路不等式，也就是说这两个不等式并不属于子回路不等式。其中，第一个不等式对应前面讲到的第一个四集合结构，只在形式上有所变化。但是第二个不等式却与之截然不同，原始论文脚注表明，Irving Glicksberg是幕后的无名英雄：“我们感激兰德公司的I. Glicksberg，他向我们指出了这一类的关系。”¹

^{1. Dantzig et al. (1954).}

Fulkerson很清楚，最好的做法也许是不要依赖特定的具体论证，就算提出论证的人是他们的朋友Glicksberg，也一样不能依赖。因此，他向TSP研究专家Isidor Heller写了一封信，信上签署的日期是1954年3月11日。他用符号“Cn”表示一道题目全体路线集合的凸包，题目包含的城市数目为n。

图6-5　George Dantzig（左）、Ray Fulkerson（中）和Selmer Johnson（右）。（照片分别由美国国家工程院、Merle Fulkerson Guthrie和得克萨斯大学美国历史中心提供）

最近，我和G. Dantzig、S. Johnson一直在借助线性规划方法研究该问题的计算特性，尽管我们并不知道，对于一般的n，路线的凸包C_n的各个面究竟如何。不过，我们使用的方法看来有望获得成功，特别是对于一道48座城市的大规模题目，我们已经通过手工计算相当快速地找到了最优路线。我们发现，根据各点所在的地图，可以方便地利用该方法对Dantzig的单纯形算法进行转换，从而确定方向相反、其他都相同的路线。例如，可以用10维空间中的25个超平面构成的系统描述C₅。我们还不太清楚C_n的一般性质，但是如果有机会读到你的论文，也许我们会学到更多。

Dantzig也向Harold Kuhn写信提出了类似的请求，时间是同一天，即1954年3月11日；他还向Albert Tucker写信求助，时间是1954年3月25日。显然，兰德公司的这几位研究者当时都在积极寻求关于TSP多面体结构的知识，以便加强割平面法的能力。

6.2.1 梳子不等式

尽管Dantzig等人发出了求助信件，但是研究界的反馈速度很慢。那个年代的科技没有现在这么发达，确实存在落后不便之处。20世纪70年代初，Vašek Chvátal终于开始重新研究这个主题。¹他得到了关于梳子不等式（comb inequality）的研究成果，推动了这方面的研究再次起步，而这距离兰德公司研究小组的原始工作已经过了接近20年光阴。Martin Grötschel和Manfred Padberg紧随其后，推广并分析了梳子不等式，为后续研究提供了效仿的样板。²

图6-6 Vašek Chvátal（照片由Adrian Bondy提供，所有权利保留）

^{1. Chvátal, V. 1973. Math. Program. 5, 29–40.}

^{2. Grötschel, M., M. W. Padberg. 1979. Math. Program. 16, 265–280.}

这里，所谓的梳子其实指的是由一系列顶点构成的一组子集，它们的关系如图6-7文氏图所示。黄色集合称为“梳柄”，蓝色集合则称为“梳齿”，梳齿之间互不相交，梳柄与每个梳齿都相交（交集非空）。我们要求，梳齿的数目k应该是不小于3的奇数。可以证明，每条回路穿过梳子各边界的次数必然至少是3k+1次，从而推广四集合结构的结论。不过证明时需要细心周密，避免遗漏某些可能的情形。

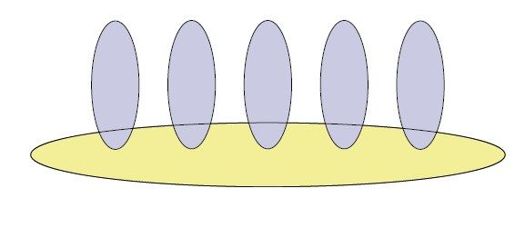
图6-7　一把有5个梳齿的梳子的文氏图

如何理解次数至少是3k+1次？仔细观察图6-8，数一数就知道了。第一幅图的梳子有5个梳齿，一条路线遍历所有顶点，与边界的交叉次数是16，也就是3×5+1。第二幅图的梳子则有6个梳齿，一条路线遍历各顶点，但是这幅图是错误的，我们不允许出现这种情况，因为6不是奇数，路线与边界的交叉次数也只有18，比3k+1规则少1，不满足要求。在梳齿为偶数的情形下，梳齿可以两两配对，不需要像奇数情形那样必须增加一次交叉才能穿出梳柄（即第一幅图路线与梳子最右侧的交叉点）。

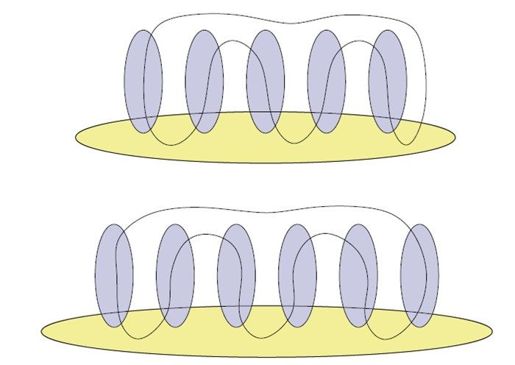
图6-8　路线穿过梳子，上图梳子有5个梳齿，下图有6个梳齿

我们已经知道，42座城市的环游美国之旅之所以能圆满完成，就是梳子的功劳。Grötschel也用梳子模型解决了另一道题目，给出了环游德国120座城市的最优路线，创下了TSP解题的新纪录。图6-9是他在解题时手工绘制的，图上不仅画出了线性规划的一个解，也表明了下一步可能用到的割平面。我们有幸欣赏这幅真实的原作：取值为1/2的边画成了波浪线，不满足子回路不等式的区域用红笔圈出，不满足梳子不等式的区域则由蓝笔圈出相应的梳柄和梳齿。每经过一轮计算，他都会向线性规划模型里增加好几个割平面——遇到大规模的旅行商问题，就应该采取这种做法，提高求解效率。

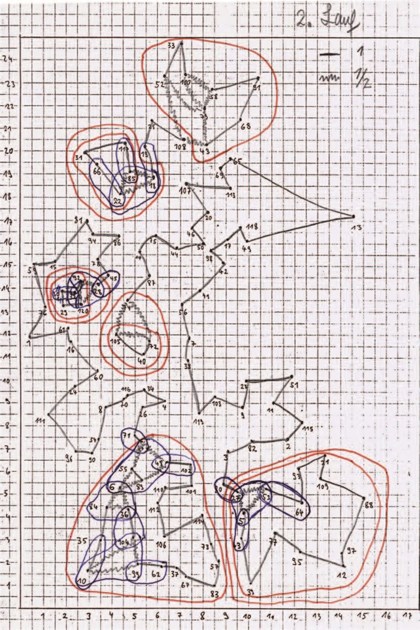
图6-9　Martin Grötschel的割平面图示，Martin Grötschel供图

6.2.2 TSP多面体的小平面定义不等式

Grötschel在计算上取得了成功，唤醒了研究界对其他类型TSP不等式的研究热情。此后，他本人与William Pulleyblank合作，率先得出了新成果，把梳子结构模型由一个梳柄的情形推广到多个柄的情形。¹多个柄的新结构称为团树（clique tree），因为满足要求的文氏图形状与树有几分相似，图6-10就是一例。

^{1. Grötschel, M., W. R. Pulleyblank. 1986. Math. Oper. Res. 11, 537–569.}

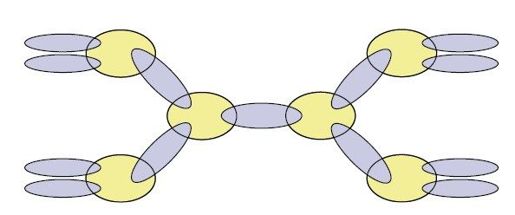
图6-10　团树

在Grötschel和Pulleyblank的研究之后，其他研究团队纷纷得到了形状比团树还要奇妙纷繁的结构。当然，奇妙纷繁只是那些不等式的表象，研究工作本身则始终没有偏离TSP多面体基本结构的路线。在高维TSP世界里，很难描述清楚TSP多面体这种几何形体，但是退回到二维平面，思路就豁然开朗了。

请考虑图6-11所示的凸包。图中画出了两个半空间，虽然它们都与集合中的至少一点相切，但是毫无异议，上面的半空间比下面的更具有本质性。事实上，在这个例子中，上面这类半空间总共只有6个，而它们合起来就能给出凸包的完整描述。这6个半空间称为小平面定义不等式（facet-defining inequality），它们围成的6条边则称为TSP多面体的小平面（facet）。

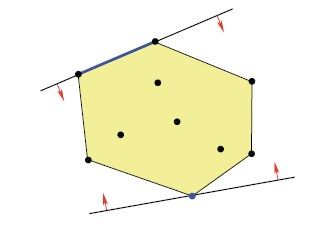
图6-11　小平面定义不等式和非小平面定义不等式

我们虽然无法画出TSP多面体的准确图象，但是这里定义的小平面概念却同样适用于高维情形。²对于TSP路线的凸包，小平面定义不等式与度约束条件可以共同给出完整描述，而任何完整描述中，这两类不等式也必然缺一不可。正因如此，我们尽管不清楚TSP多面体的完整结构，依然可以得出肯定的结论：在任何一组能够恰好紧紧包围住路线集合的不等式之中，必然存在某些特定的公共不等式。

^{2. 为证明一个不等式是小平面定义不等式，可对满足不等式的回路方程进行分析。选取包含这些路线对应点的最小平面，验证它所处的空间维度恰好比TSP多面体空间维度小1。二维空间的例子便是如此，小平面上的两个顶点决定一条直线，而直线也就是一维平面。}

20世纪50年代，Harold Kuhn和其他人都研究过小TSP多面体的小平面。但首先倡议研究界关注小平面定义不等式的并不是他们，而是Grötschel和Padberg。³这两人当时正在构造有可能性的割平面列表。

^{3. Grötschel, M., M. W. Padberg. 1979. Math. Program. 16, 265-280.}

我们对证明该事实的兴趣基于两个方面：首先，在提出的这些不等式中，哪些对于定义这个极为复杂的多面体有真正重要的意义，获知这个问题的答案是富有数学趣味的；其次，按整数规划的意义理解，小平面是“最强的割平面”，因此我们自然会猜想，这些不等式对于获得这道组合最优化难题的数值解也具有至关重要的计算意义。

Grötschel和Padberg共同证明了子回路不等式和梳子不等式都是小平面定义不等式，而Grötschel又和Pulleyblank一起证明了团树不等式也属于这一类“精英不等式”。

整个20世纪90年代，小平面一直是研究的热点话题，领军人物是法国格勒诺布尔的Denis Naddef和意大利罗马的Giovanni Rinaldi。⁴这段时期的研究成果非常丰富，大量信息至今尚未在计算科学领域得到充分利用。尽管如此，我们对于TSP多面体的了解仍然非常有限，距离彻底认识仍有很大差距：10座城市的多面体就已经发现了足足510亿个小平面，而现有的一般性理论只能解释其中的一小部分。说得乐观一点，该领域仍有大量信息等待后来者发现，为未来的TSP研究提供了充足的研究目标和发展空间。

^{4. Naddef, D. 2002. In: G. Gutin, A. Punnen, eds. The Traveling Salesman Problem and Its Variations. Kluwer, Boston, Massachusetts. 29–116.}

图6-12　左图：Egon Balas、Suzy Mouchet-Padberg、Harold Kuhn、Manfred Padberg和Martin Grötschel（2001年摄于德国柏林，照片由Martin Grötschel提供）；右图：Giovanni Rinaldi和Denis Naddef（2008年摄于法国Aussois，照片由Uwe Zimmermann提供）