7.2 搜索队

Eastman的研究工作带来了一种搜索策略，TSP研究者Little等人将其命名为分支定界法。¹思路非常直截了当。首先从原问题出发，原问题也称为根松弛问题 （root relaxation）。对于某个子问题，只要由它得到的线性规划下界大于等于一条已知路线的长度，就舍弃该子问题，以后均不予考虑。每一步，我们都选择一个剩下的子问题，进行分支操作，得出两个新的子代的子问题。以上过程重复进行，直到每个未分支的子问题均被修剪舍弃为止。

_{1. Little, J. D. C., et al. 1963. Op. Res. 11, 972–989.}

分支定界法说起来简单，但受到很大局限，只有优秀的定界机制才能保证计算成功。弱的下界会导致搜索树非常庞大，反之，强的下界则能实现快速修剪舍弃，从而快捷求得最优解。Eastman本人并没有考虑到要用割平面法改进度约束下界，因此他的计算结果虽然成功，规模却不大。在博士论文里，他只解决了一道10座城市的例题。

相比之下，图7-3的规模则大得多。该图展示了如何利用分支定界法解决环游美国42座城市的问题，根松弛问题是长度为687.5的线性规划模型，每次在未修剪的子问题中出现子回路时，都加入约束条件使之消除。我们效法Eastman的先例，用树的形式展示整个搜索过程，子代的子问题与父代的子问题之间直接相连。请注意，每步分支操作之后，子代子问题对应的线性规划下界都会产生实质性改进。这样的结果正符合我们的心意。

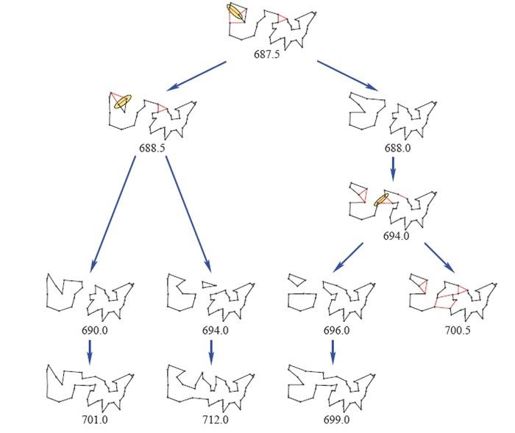
图7-3 环游美国42座城市问题的分支定界搜索树

7.2.1 分支切割法

尽管割平面法和分支定界法起初曾经彼此较劲，这两种方法本质上却是天生一对。实际上，20世纪80年代，研究者将两者结合起来，一时轻松横扫天下。当时的领军人物是Manfred Padberg和Giovanni Rinaldi。他们创造了“分支切割法”（branch-and-cut）这个新词，给出了谨慎细致的程序实现，让旅行商的计算过程突飞猛进。随着一道2392座城市的测试实例宣告破解，他们突破了之前的所有计算纪录。¹

_{1. Padberg, M., G. Rinaldi. 1987. Oper. Res. Let. 6, 1–7.}

Padberg和Rinaldi在计算中并没有对割平面法施加人为限制，而是恰恰相反，尽情使用所有能用的割平面，想方设法改进线性规划模型。他们由此发现了一种有用的处理方法，就是建立一个库（pool），把每次切割都保存在其中，以供所有子问题共用。换言之，如果一个割平面能够改进一个子问题的线性规划下界，那么研究者就把它存起来，等到处理其他子问题时也许能派上用场。建立这个库是出于两方面的考虑。第一，搜索该库的速度会比执行复杂分离算法的速度快得多。第二，TSP计算用到的绝大多数分离算法都是试探性的启发式算法，有时它们试探不中某道子问题，却能试探中另一道子问题。因此，我们可以通过把不等式集结成库，整理出所有正中目标的试探，看看它们能对搜索树的其他部分起到什么作用。

7.2.2 强分支

Vašek Chvátal喜欢把分支步骤比作结婚。一旦决定进行分支，就意味着承诺使用分支后的新观点看待问题。分支之后，便不可能回头。按照他提出的比喻方式，可以认为，分支定界法的早期研究者一般都使用一见钟情式系统，会与路上遇到的第一个潜在结婚对象结为伴侣。这也就是说，他们只要看到线性规划解中有条边取分数值，就会立刻以这条边为分支标准，将原问题一分为二，得到一对子问题。这种分支方法速度够快，但是在分支定界法里，定界过程也要耗费大量时间，所以有必要多花点工夫，认真选择分支边。Padberg和Rinaldi的做法用到了一种技术，可以比作利用婚姻介绍所甄选潜在的伴侣。在Concorde程序里，我们又加了一步，计划在做出选择之前，首先跟数名候选对象出去约会几次再说；然后我们“全面发展”，决定在最终正式进入婚姻殿堂（分支）之前，先和最好的几个人选同居一阵子再做结婚承诺。

下面从第一步的婚姻介绍所开始解释。Padberg和Rinaldi采用统计学方案，构造出一组分数化程度最高的边，即取值距离0和1都很远的边。在这一组边中，他们选出旅行成本最高的一条边。此举理由充分，因为与短边相比，在长边上进行分支往往对线性规划的界影响更大。

Concorde程序的思路称为强分支（strong branching）：对于单纯形算法可能得到的数值，要求线性规划解题程序给出强有力的提示，从而降低选择步骤的猜测程度。对于候选分支边对应的每一对子问题，解题程序执行有限次数的单纯形换主元操作，比如进行50步，据此给出提示。我们参考并比较这些数值，判断哪种情况对线性规划的界改进最为明显，就选择相应的分支。这步计算过程可能花费相当长的时间，但只要能避免错误拆分问题导致搜索树大小加倍，即便多花些工夫也是值得的。

“全面发展”之所以能改进结果，是因为这一步选定了强分支挑出的少数优秀人选，然后实际解决相应的线性规划子问题，包括对于每个可能的子问题应用有限个割平面。该过程能准确预期得到的线性规划的界，但是需要付出高昂的计算代价，只有最难的例子才值得如此求解。正统数学家大概会说，这样做是在投机取巧，因为最终做决定之前已经试验过各个分支的结果。可是为了对抗旅行商，我们所做的一切都属于光明的正路。