4.3 改进路线？立等可取！

1985年4月，美国《发现》杂志刊登了一篇介绍TSP的文章，作者是马丁·加德纳（Martin Gardner），插图漂亮地画出了环游美国的路线，如图4-15所示。《发现》杂志读者众多，马丁·加德纳也是家喻户晓的解题高手，强强联手推出的文章自然使旅行商广受关注，但也在读者中引起了骚动。仔细观察图4-15，你会发现骚动的原因——这条周游所有城市的路线显然有好几处可以缩短！

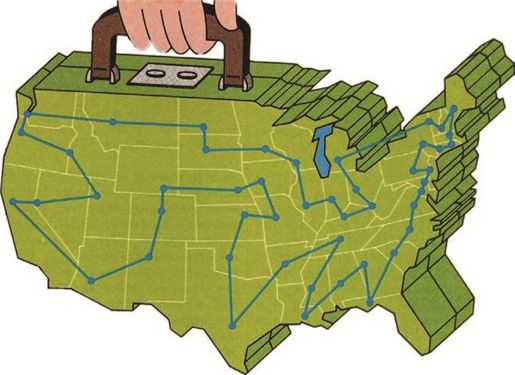
图4-15　环游美国的路线，Nina Wallace绘制

《发现》杂志，1985年4月，第87页

文章刊出之后，加德纳与IBM公司的数学家Ellis Johnson通过电话。在电话中，他解释说，路线的来源其实是Dantzig等人的论文。文章的问题并不在于路线本身，而是因为编辑画蛇添足，自作主张把各城市挪到了各州首府的位置。那幅插图的说明文字是这样的：“旅行商问题是数学界最古老的未解之谜之一。这里是旅行商周游48个州的首府的最短路线。”加德纳真倒霉。当初在1954年，Dantzig等人只是为了方便而选择了那些城市，结果加德纳却因此必须赶紧做出更正，所以他才给Johnson打了电话，Johnson介绍他向TSP专家Manfred Padberg求助。

Padberg当然有能力解决这道周游48州首府的问题，然而当时似乎无法联系到他本人。最终出手相助的是贝尔实验室的Shen Lin。在Gardner的文章发表4个月后，Lin提出了一条新的路线，也发表在《发现》杂志上。他虽然没有准确求解路线的算法，却是路线改进方法的专家。

这一回，杂志描述路线时非常谨慎。“他的答案对吗？Lin本人对此确信无疑，甚至提供了100美元的奖金，悬赏征求短于10 628英里（约17 104千米）的旅行商路线，要求周游各州首府并使用他给出的数据计算。”编辑向任何有意接受这一挑战的读者提供了一张距离数据表，不过Lin不用担心破财，因为他的路线确实是最优路线。

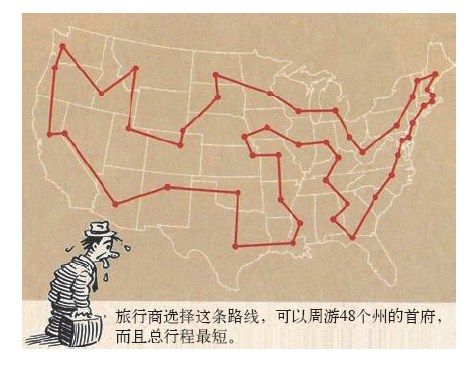
图4-16　环游美国的最优路线，Ron Barrett绘制

《发现》杂志，1985年7月，第16页

4.3.1 边交换算法

Lin倡导使用路线改进算法。这类算法名副其实，读取一条路线后，便会查漏补缺，对其调整修正。以《发现》杂志第一篇文章中的TSP路线为例，它在进出田纳西州时形成了一个尖角，表明这部分路线有问题。局部调整修正方法如图4-18所示。首先删掉形成尖角的两条边，同时删掉它们正北方（图中正上方）紧邻的一条边，将路线分为3段，其中一段就是田纳西州首府这一个孤立点。然后再连接3条新的边，将路线连为一体。新添的边用红色表示。由于三条新边的长度之和远远小于3条旧边，因此路线得到了改进。这步操作相当于交换了3条边，因此称为3-交换（3-opt）。

图4-17　Shen Lin，1985年（照片由David Johnson提供）

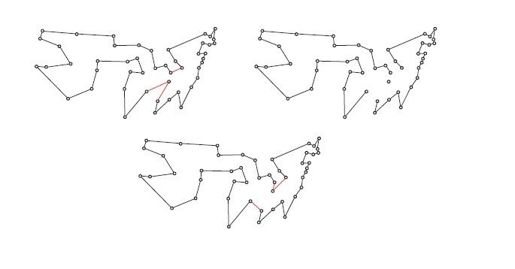
图4-18　通过一步3-交换改进《发现》杂志的TSP路线

Lin在计算这道题目的过程中，全面探寻了可以改进路线的方法，包括2-交换、3-交换和更多边的交换操作。2-交换的步骤就是删除路线中的两条边，用另外两条更短的边重新连接路线。首次尝试求解42座城市的环游美国问题时，我们曾按照最近邻算法构建了一条大大需要改进的路线，现在就以此为例探究Lin运用的解题思想。

TSP领域，最基本的定理可能要数这一条：如果题目数据使用欧几里得距离，那么最优路线必定不会自交。用一步2-交换就可以证明这个事实，因为删除一对相交边、重新连接相应点之后，总路线必然会缩短。如图4-19所示，一步2-交换使总路线长度减小为982个单位长度，缩短了31个单位长度。这步交换非常明显，而且图上仍然有多处可以进行此类交换。

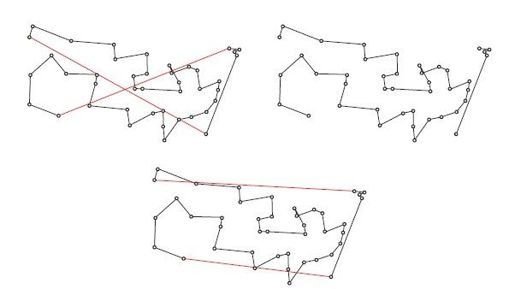
图4-19　可以改进最近邻路线的一步2-交换

接下来，我们反复使用2-交换改进路线，最终得到的路线如图4-20所示，总长度为758个单位长度。这时总共进行了27次2-交换，已经无法通过这种操作进一步改进路线了。但是我们发现，通过交换两条边的简单操作，就大大改进了差劲的最近邻路线，如今它只比最优路线长8%而已。

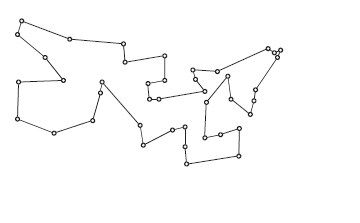
图4-20　无法通过2-交换进一步改进的路线

图4-21　Shen Lin和Brian Kernighan，Bell Labs News，1977年1月3日（Brian Kernighan供图，Alcatel-Lucent USA Inc.授权复制）

4.3.2 Lin-Kernighan算法

我们要前进到底，所以接下来可以考虑所有能够改进路线的3-交换，然后是4-交换，再然后是5-交换，以此类推。20世纪60年代中期，Lin确实发表了结果，证明3-交换可以成功地改进路线。但是，如果k远远大于2和3，搜寻改进路线的k-交换就需要巨大的计算量，因此完全不可行。尽管如此，Lin和计算机科学先驱Brian Kernighan还是成功实现了这种方法。¹他们巧妙地构建了一种新算法，取得了TSP研究中最伟大的成就之一。

^{1. Lin and Kernighan (1973).}

Lin-Kernighan算法（简称LK算法）精巧复杂，但图4-22足以概述其中心思想。该图将初始路线表现为一个环，降低了理解算法流程的难度。需要提醒读者注意，各边在图中的长度并不代表实际路程。

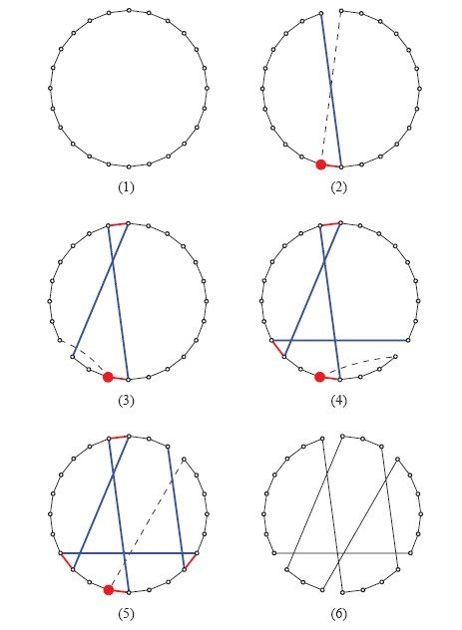
图4-22　使用Lin-Kernighan搜索算法寻找k-交换

搜索的第一步如图4-22的小图（2）所示。首先选定一座城市作为根据地，图中用红点表示；然后选择一条与之相连且属于初始路线的边，图中以红色表示；再从这条边的另一个端点出发，选择一条不属于初始路线的边，图中以蓝色表示。算法意在删减红边，增加蓝边，因此仅考虑蓝边的代价低于红边的情形。这一步也可以进行图示的2-交换操作，删除路线中与蓝边远端相连的合适的边，并连接该端点与根据地之间的边，从而用蓝边替换红边，即改变路线。如果这步2-交换可以改进路线，那么很好，我们就把具体改进数值记录下来。但是接下来还要继续搜寻，希望能找到更大的改进。

如图4-22的小图（3）所示，第二步是把刚才考虑删除的边染成红色，并选取不同于刚才考虑连接的边的另一条蓝边。此时，依然仅考虑两条蓝边的代价之和低于两条红边的情形。同样，也可以删除路线中与蓝边远端相连的一条边，增加直接回到根据地的边，如虚线所示。同样，如果这步可能的3-交换可以对路线做出迄今最好的改进，那么我们就把改进的数值记录下来。

搜索继续以蓝边总代价低于红边总代价为前提，考察成对的红边和蓝边。如果到达路线终点，无法增加新的一对蓝边和红边，就回溯到早前的某级端点，继续探寻其他可选的蓝边。该算法最终有两种可能的结局：要么由于时间因素而中止搜索，要么由于已经考虑过所有可能的边而终止搜索。

总之，在搜索结束时，我们选取已记录的改进最大的交换操作，以此改进路线，再对改进后的路线重新开始新一轮搜索。如果找不到有改进的交换操作，则重新选择根据地，再次从初始路线出发尝试搜索。

只需每次选择红边和蓝边，再检查直接回到根据地的边，如此重复即可。乍一听易如反掌，然而细节里暗藏无数玄机。幸好，Lin和Kernighan不仅计算出了出色的结果，还深入浅出地阐述了用于实现与改进该算法的诸多思想。过去40年间，在他们两人的原始论文的指导下，Lin-Kernighan算法得到了精确的设计和落实。新近开发的此类软件能力更强，能够解决超过千万座城市的大规模TSP题目，求出非常优秀的路线。

对于环游美国问题的数据集，以图4-20中经过反复2-交换得到的路线为初始路线，使用Lin-Kernighan算法的解题步骤如图4-23所示。该算法在五次迭代之后找出了最优解，每一步所得路线中红边所示的路段都将在下一轮搜索中被删除。

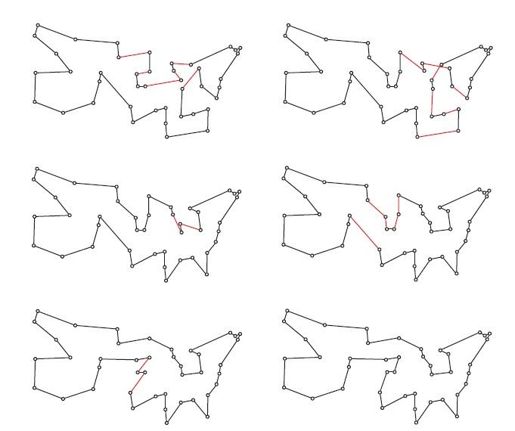
图4-23　Lin-Kernighan算法求解环游美国问题的五次迭代

Lin和Kernighan在原始程序中使用随机路线作为初始路线，结果同样得到了环游美国问题的短路线，这本来就在意料之中。“对于中小规模的题目，比如环游42座城市问题这么大的规模，一次试验得到最优解的概率接近1。”²然而后来的结果却出人意料，卓越非凡。他们设计这一基本方法原本只为解决几十或几百座城市的TSP题目，却为过去几十年中大多数优秀TSP启发式解法奠定了基础，在此期间，规模大得多的题目也获得了解决。

^{2. Lin and Kernighan (1973).}

这里必须指出，k-交换方法虽然在应用中表现出了优秀的性能，在理论上却无法保证优良的最差情况性能，实属不幸。以反复进行2-交换的方法为例，对于满足三角不等式的题目来说，该方法只能确保路线长度不超过最优解的4√n倍。³这是Lin-Kernighan算法的缺点所在。即便如此，使用该算法时也不必过分担心，因为它是算法中的王者，一般情况下都确实能够得到非常好的解。

^{3. Chandra, B., H. Karloff, C. Tovey. 1994. In: Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms. SIAM. 150–159.}

4.3.3 Lin-Kernighan-Helsgaun算法

Lin-Kernighan算法在实际计算领域长期占据统治地位，得力于研究界对它持续不断的改进和增强。尽管多数改动只是在原有想法的基础上进行细微的调整，但是1998年，计算机科学家Keld Helsgaun却带来了一枚重磅炸弹。

Helsgaun的主要贡献是重写了算法的核心搜索程序。此前25年间，这部分内容几乎一直原封未动。Lin-Kernighan标准算法可以视为搜寻2-交换操作序列的方法，Helsgaun的新方法却以5-交换操作序列为搜寻对象。换言之，他没有沿用一条红边一条蓝边的逐步搜索模式，而是发明了一种新的方案，每次同时考虑5条红边和5条蓝边，总共10条边。

10条边。看到这个，你的第一反应想必是：“边数可真够多的。”没错，如果考察5条红边、5条蓝边的所有可能情形，确实会严重拖慢算法速度。为避免这种结果，Helsgaun对搜索加以限制，只考察能由连续5步搜索得到的红边、蓝边组合，该过程中并未要求每步的蓝边代价之和必须低于红边。他的方法每次都一下子考虑所有此类5-交换，因此能够发现原有标准算法完全找不到的改进操作。

新算法名为Lin-Kernighan-Helsgaun算法，简称为LKH算法。它以5-交换操作为核心，还借用了大量各类技巧，树立了探寻路线方法的新标杆。“对于含有100座城市的一般题目，给出最优解只需不到一秒钟；若含有1000座城市，则只需不到一分钟。”¹当时人们认为该领域的研究已经相当成熟完善，但LKH算法还是在实际性能方面实现了如此惊人的飞跃。

^{1. Helsgaun, K. 2000. Eur. J. Oper. Res. 126, 106–130.}

4.3.4 翻煎饼、比尔·盖茨和大步搜索的LKH算法

人们得知Helsgaun构建了许多知名难题的改进路线后，纷纷猜测他在实际计算中是如何成功实现5-交换策略的。为使读者理解其原因，在此有必要指出，在Lin和Kernighan发表原始论文之后、LKH算法公布之前的25年时间里，实现标准LK算法的有效程序代码屈指可数。LK搜索算法虽然有清晰明确的解释表述，但难以转化为能处理大规模数据集的软件。

LK算法还可以用难来形容，但LKH算法看起来简直是不可能实现的。事实上，LK算法按照红边、蓝边交替顺序搜寻路线，具有一大特色，即在搜寻的每一步，回到根据地城市的路线都仅有一条。换句话说，如果从一条完整路线中删除两条边形成两条子路线，那么把它们连接起来形成新路线的方式是唯一确定的。然而LKH算法却不同，简单计算可知，每一步5-交换操作都来自连续五步2-交换，涉及5条子路线，连接形成新路线的可能方式便有148种之多。所以LK算法和LKH算法之间的差别，就是1和148之间的差别，也就是难和特别特别难之间的差别。

Helsgaun向研究界公开了完整的程序代码，以此揭示了他取得成功的秘诀。Dave Applegate和我通读了他的文件，结果发现其中根本没有真正的独门秘诀可言：他的代码里完整列出了148种情形，分别讨论了所有的可能性。他为了写出正确可行的代码，实现极为复杂的算法，付出了堪比愚公移山的努力。

Helsgaun的代码令人动容，LKH算法的性能振奋人心，但人们还是好奇，把5-交换改为6-交换能否进一步优化结果。Applegate写了一个小程序，计算出连续得到的6-交换会产生1358种重连路线的可能方式。这样的数字已足以令人望而却步，但每次交换的边数更大会怎样呢？升级到9-交换的时候，要面对的可能情形已高达2 998 656种，确实会相当费劲。

不过，其实还有一线希望。Applegate的小程序能够逐一列出所有可能的重连方式，而仔细考察LKH算法可以发现重连方式的规律。因此，我们结合这两方面内容，能够设计出一个计算机程序。对于任意k，这个程序都能提供解决k-交换操作的实际代码，也就是说用一个程序生成另一个程序。

这个主意似乎不错，实际上产生的代码非常长：6-交换的代码有120 228行，7-交换的代码有1 259 863行，8-交换的代码有17 919 296行，全都是用C语言编写的。尽管把这些代码编译为计算机可以识别的2进制语言并非易事，不过生成的程序确实可以运行，而且得到了有趣的结果。8-交换是能够实现的上限，效果却并不比5-交换更让人满意。而对于9-交换而言，根本不可能生成完整列表逐一讨论所有情形。

Applegate毫不气馁，勇往直前。他想到，如果采用这种母程序生成子程序的方法，提高母程序的工作效率，就不必逐一列举出所有情形。具体说来，母程序可以在执行k-交换搜索的同时，提供每种情形的应对步骤，从而生成子程序代码。这样一来，虽然执行搜索步骤所需的计算时间仍然是限制因素，但是有机会实现每次交换更多边数。加快生成程序计算速度的研究与翻煎饼问题¹密不可分。微软公司的比尔·盖茨（William Gates，常称为Bill Gates）本科就读于哈佛大学，他在校时曾和TSP专家Christos Papadimitriou共同研究过这一类问题，此事众所周知。翻转煎饼堆顶部的一叠煎饼对应于反转TSP路线中的一段子路线，也就是2-交换操作。因此，要想实现能够生成k-交换程序的母程序，首先要有一个算法，能够找出按照k-交换顺序重排路线最少需要反转几次。这正是Gates-Papadimitriou的研究成果的变形。²我们经过努力实现了这种算法，得到了连续k-交换的高效动态搜索机制。

^{1. 翻煎饼问题是指，有一堆大小不一的煎饼叠放在一起，希望通过翻转把煎饼按照从小到大的顺序从上到下排列，要求编写翻转的算法或程序。每次翻转时，把铲子插入两块煎饼之间，铲子上方的煎饼整体上下翻转，使铲子上最下层的煎饼翻到顶上，而原来顶上的煎饼则落到插入铲子的地方，铲子下方的煎饼没有变化。参见http://poj.org/problem?id=2275。——译者注}

^{2. Gates, W. H., C. H. Papadimitriou. 1979. Discrete Math. 27, 47–57.}

Helsgaun后来对LKH程序进行了有力的升级，在新的代码中引入了类似的思想，允许用户具体指定每次交换操作包含连续几步。2003年，为了展示新软件的效力，他以周游瑞典24 978座城市的问题为例，计算了10-交换操作，所得TSP路线的最优性于次年得到证明。