7.1 拆分

在线性规划的松弛问题里寻找最优路线，就像是在干草堆里寻找最精细的针一样。如果有充足的不等式和耐心，割平面法也能解决问题，把上面的干草都移走，让那根要找的针最终脱颖而出，在干草堆顶上闪闪发光。

虽然听起来不错，可惜有时候事情并不尽如人意，有可能每次新加入割平面都只能移走一点点干草。此时，我们便可以放弃继续在剩下的干草堆上“割”来“割”去，转而考虑把大草堆“分”成两垛小草堆。如果拆分方式合理，那么解决新得到的两个子问题就会比原先搜寻整垛大草堆更容易，也就能在干草堆和所有针之间理清头绪。这个拆分步骤称为分支（branching）。Dantzig等人描述了一般情况下的分支思想，后来Willard Eastman根据该理念提出了完整的TSP算法¹。

_{1. Eastman, W. L. 1958. Linear Programming with Pattern Constraints. Ph.D. thesis. Department of Economics, Harvard University, Cambridge, Massachusetts.}

我们将在下一节介绍分支定界算法。这里首先以42座城市的环游美国问题为例，深入探讨其中的一步分支操作。对于这道题目，本来只用割平面法就足以轻松给出答案，所以，我们人为施加限制，只允许使用一类割平面，也就是对应于线性规划解中孤立子图的子回路不等式。这样一来，第6章列出的前三步计算仍然可以照常进行，得到的下界为682.5个单位长度，连通图如图7-1所示。

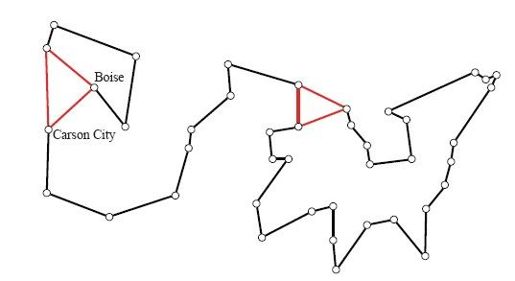
图7-1　增加3个子回路消去约束之后求得的解

至此，图7-1中的线性规划解相当于草堆顶部露出来的一束干草。因此，合情合理的分解问题方式至少应该把这个解移走。标准做法非常简单，只需要选取一条红边，并要求题目必须在“使用”与“不使用”该红边之间做出选择。也就是说，我们把路线集合一分为二，用到该红边的路线属于第一个子集，而不包含该红边的路线则属于第二个子集。在线性规划模型里，这种方法效果很好，因为只需要加入约束条件x_ij=0就能得到第一个子问题，加入x_ij=1则能得到第二个子问题，其中城市i和城市j是该红边的端点。新生成的两个子问题分别称为分支的0侧（0-side）和1侧（1-side）。

在环游美国之旅的例子中，我们选择Boise和Carson City之间的边作为分支边，得到的线性规划解如图7-2所示。请注意用黄色区域标出的这条分支边，分支0侧的线性规划解里不含该边，而分支1侧的线性规划解里含有该边。单纯形算法再一次给出了正确答案。0侧解对应的目标函数取值为687.5，而1侧解对应的取值为676。由于每条周游42座城市的回路同时都是两个线性规划模型的可行解，我们知道，所有路线取值都不可能低于686个单位长度。

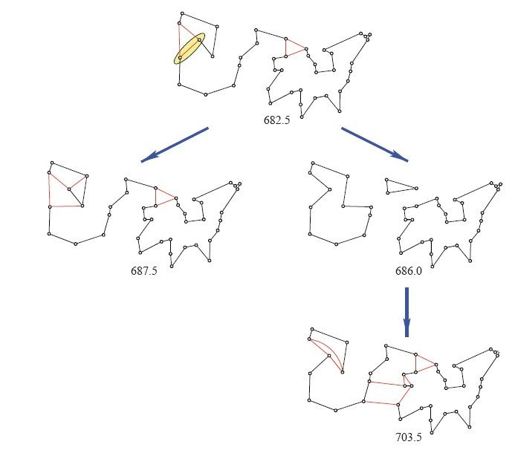
图7-2　选择连接Boise和Carson City的边进行分支操作

这一步分支操作不但把解的下界从682.5提高到了686，而且还有进一步的好处：在1侧的线性规划解中有几个孤立子图，只需加入几个子回路消去约束就能收拾干净，得到一个新的线性规划解，长度为703.5，见图7-2的右下角。很好。我们既然已经知道有条路线长度只有699，那么继续寻找潜在更优路线的过程中，就没有必要再看分支的这一侧了。由此，我们可以直接去掉1侧的子问题，也就是“修剪”掉一个分支，以后搜寻最优路线就不再考虑这一部分的解。

总而言之，我们首先把干草堆一分为二，接着向模型中添加若干个割平面，然后在两个小草堆中舍弃一个。并不是所有时候都能出现这么理想的形势变化，不过这个例子应该足以让你相信，在TSP求解过程中，分支法的确能够发挥很大的用处。