5.4 TSP对应的度约束线性规划的松弛

线性规划方法问世之后，没过多久就打入了旅行商的世界。Dantzig与Hotelling和约翰·冯·诺依曼的那段往事发生在1948年9月9日，而在次年秋天，Julia Robinson就公布了第一个基于线性规划的TSP解法。

在表面上看来，TSP似乎与Dantzig发明的通用经济统筹方法并不契合。事实上，如果你把五名TSP研究者关在一间房子里，让他们解释为什么线性规划方法是TSP的自然求解思路，最后很可能会得到五种截然不同的答案。我个人最欣赏的线性规划的理解方式如本章开篇一段所述，也就是将所有路线都满足的若干简单基本规则结合在一起，从而获得路线的品质保证。

在对偶性的脚本上，这一切写得明明白白：藉由对偶变量的赋值，规则之间相互结合；而通过弱对偶性定理，品质保证便水到渠成了。

让我们看看实际应用如何吧。按照之前的惯常做法，我们考虑对称的TSP，也就是旅行成本与旅行方向无关的情形。读者想必已经很熟悉用来描述这种题目的图论术语了，顶点代表的是城市，边代表的是城市间的道路。路线就是选择的一组边，这些边合起来构成一条哈密顿回路，如图5-2所示，图中给出了24座城市的完全图，红线表示一条选定的路线。

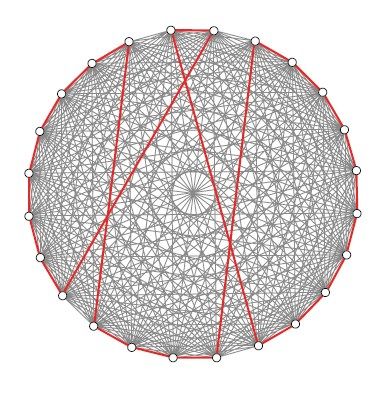
图5-2　完全图某条路线的边

画图的时候，完全可以用灰线和红线表示，但是用数学语言描述题目时，最好还是给边赋值0和1来表示两种情况：赋值为0的边不在路线里，而赋值为1的边在所给的路线中。

图5-2的例子有24座城市，因此有276个这样的值。数值太多了！如果要仔细考虑，我们难免会困在一大堆记号里动弹不得，所以我们先简化题目，看看更原始的图5-3。这里只有区区6座城市，为了确定一条路线，需要15个值。我们把连接每对顶点i和j的边所取的值记为x_ij，具体说来，这15个值分别为x₁₂, x₁₃, x₁₄, x₁₅, x₁₆, x₂₃, x₂₄, x₂₅, x₂₆, x₃₄, x₃₅, x₃₆, x₄₅, x₄₆, x₅₆。这些就是线性规划模型中的变量，它们量度的是路线是否用到了对应的边，如果你愿意的话，也可以把它们理解为某种“经济活动强度”。

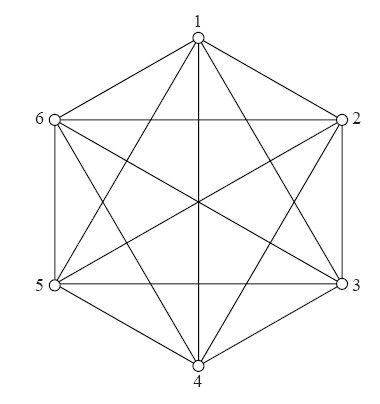
图5-3　6个顶点的完全图

我们把每对城市之间的旅行成本记为c_ij，这样一来，如果某条边在路线中，那么相应的c_ij乘以x_ij就等于c_ij，反之则该式取值为0，一条路线的总成本便可记为线性表达式c₁₂x₁₂ + c₁₃x₁₃ + …+ c₅₆x₅₆。这就是我们在TSP的线性规划模型中需要最小化的目标函数。至此，我们已经确定了变量和目标函数，那么约束条件如何得到呢？

哎呀，大事不妙，我们可没法直接说条件就是挑出一条路线作为解。要想使用线性规划方法，就必须严格遵照Dantzig建立的模型，严格使用线性规则。寻找合适的线性规则是我们的解法的核心之道。

5.4.1 度约束条件

开始求解时，疯帽匠指出，线性规划中的每个变量都必须是非负数。没错，可是这没什么实际效果。要想真正有所进展，我们必须仔细观察，图的边组成的子集中，能够形成路线的子集究竟有何特别之处，因为有的子集能够形成路线，有的却不能。如何利用线性约束条件区分这两种子集呢？

Julia Robinson的研究便是以此作为出发点的。她注意到，在任何路线中，图的每个顶点都恰好与两条边相连。这条规则本身并不是线性规则，不过由此可以推出，如果把经过给定顶点的所有边的x_ij值相加，那么得到的和必然恰好为2。因此，我们对任何一座城市都有一个度约束条件（degree constraint），从而得到线性规划模型。

目标：c₁₂x₁₂ + c₁₃x₁₃ + …+ c₅₆x₅₆取最小值

约束条件：

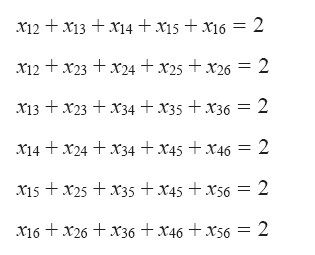
(i,j)是任意一对顶点，且x_ij≥0

上述模型称为TSP对应的度约束线性规划的松弛（degree LP relaxation）。

上述松弛的最优解本身往往未必是完整路线，即便如此，它依然能够提供宝贵的信息。事实上，每条路线都是线性规划的可行解，所以最优的线性规划目标函数值必然不会超过最优路线的成本，这是运用线性规划解决TSP时最需理解和领悟的重点所在。对于TSP对应的线性规划问题，我们在一大堆可行解中选择最优解，从而获得路线可能成本的一个下界，数值为X。任意路线的成本都绝对不可能低于X，就像之前我们确信产品利润绝对不可能超过450美元一样。

5.4.2 控制区

上述给出界限的思想非常重要，值得再次细细品味。所以，下面我们换种角度，重新审视度约束线性规划的松弛。这一次，我们直接研究对偶问题，采取由Michael Jünger和William Pulleyblank提出的思想，用一种漂亮的技巧处理TSP的几何题目。¹在本节的说明中，我们假定TSP题目的旅行成本是各点之间的直线距离。

^{1. Jünger, M., W. R. Pulleyblank. 1993. In: S. D. Chatterji et al., eds. Jahrbuch Überblicke Mathematik. Vieweg, Brunschweig/Wiesbaden, Germany. 1–24.}

首先，假设以一座城市为圆心、以r为半径画一个圆盘，使圆与其他所有城市都不接触，如图5-4所示。无论路线如何，旅行商必定会在旅程中的某一刻到达这座城市，为此，他到达和离开这座城市时都必须至少经过距离r。我们由此可以得出结论，每条路线的长度至少为2r。进一步，我们可以以每座城市i为圆心、分别画一个半径为r_i的圆盘，只要它们互不交叉重叠即可，如图5-5所示。这样一来，任何TSP路线的长度都不短于所有圆盘半径之和的两倍，我们便得到了路线长度的一个下界。Jünger和Pulleyblank将这些圆盘命名为控制区（control zone）。

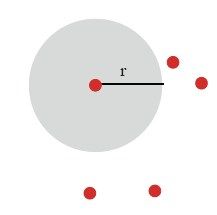
图5-4　1个控制区

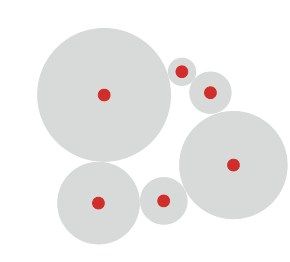
图5-5　6个控制区

图5-6　Michael Jünger（左），Regine Strobl摄；William Pulleyblank（右），Nick Harvey摄

我们希望控制区给出尽量大的下界，为此，有必要适当选择各个圆盘的半径，在互不交叠的前提条件下，使圆盘半径之和的二倍取最大值。无交叉无重叠的前提条件可以简洁地表示为：对于每对城市i和j，它们对应圆盘的半径r_i与r_j之和不得超过城市之间的距离，即r_i与r_j必须满足

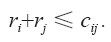
由此可见，为了获得最好的一系列控制区分布，要解决如下的线性规划题目。

目标：2r₁ + 2r₂ + 2r₃ + 2 r₄ + 2r₅ + 2r₆取最大值；

约束条件：

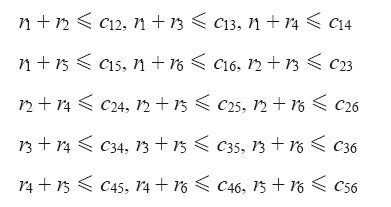
满足上述模型的任何可行解都给出一组互不交叠的控制区分布，所以同时也给出原题的所有TSP路线长度的一个下界；最优解给出的控制区下界是最强的。

读到这个命题，你也许回想起了之前提到过的弱对偶性定理。的确，控制区分布问题正是度约束线性规划的松弛问题的对偶问题！何以见得？只需注意到，对偶问题中每个顶点i都有一个系数y_i对应于第i个度约束条件。当我们分别用y_i乘以相应的约束条件，将它们加在一起时，得到的线性表达式中，每个变量x_ij前的系数必然不会大于c_ij的值。由于变量c_ij出现在第i个和第j个约束条件中，因此，我们便要求y_i+y_j≤c_ij。这个式子正是上面的互不交叠条件，唯一区别只是半径r_i改用y_i表示而已。

当然，我们必须承认，这里有一点投机取巧了。实际上，对偶线性规划问题允许控制区的半径取负数值，原因在于度约束条件是等式而非不等式，所以用负数与等式相乘也是完全合理的。不过，我们只是为了严谨起见而指出这一点，它对结果并没有影响，因为虽然在上面的题目中并未直接限定取值为非负数，但是根据三角不等式可以证明，必然存在一组最优的对偶系数，使得每个系数取值都是非负数。