6.3 TSP不等式的分离问题

现在我们面前有一大堆不等式，任何有意接受TSP挑战的勇士都可从中自由选用，不过，高效利用这些不等式可没那么容易。事实上，如果要继续推进TSP研究，这个问题就应当重视。

我们的研究任务是分离问题（separation problem），也就是说，要从已知的TSP不等式中，找到给定的线性规划解不满足的不等式。可以认为，这些不等式对应的半平面将给定的解从路线的凸包中“分离”出来，该问题正是因此而得名。分离是割平面法的核心问题——Concorde之类的TSP求解程序的实质只是调用分离程序的打包程序而已。所以，假如你希望加入TSP的盛会，那么研究又快又省的分离方法绝对是不二法门。

6.3.1 最大流与最小割

在割平面法中，各种子回路消去约束条件犹如工蜂，任劳任怨，尽职尽责。至少，在子回路消去约束层面，分离问题已经得到了充分的认识。这里用到的技巧方法可追溯至冷战年代，当时有两拨数学家关注过东欧铁路系统，一方的研究内容是利用铁路运输装备，另一方的研究方向则是如何“卓有成效”地发起轰炸从而摧毁铁路网。¹

^{1. Schrijver, A. 2002. Math. Program. 91, 437–445.}

我们不打算就此转向欧洲，还是继续看42座城市的环游美国TSP吧。请再次仔细考察加入前7个割平面之后得到的线性规划解。图6-13给出了对应的线性规划图解，我们用四种不同颜色指明了四条通路，它们均从南方的Phoenix出发，汇集于北部的Montpellier。设想要沿着这四条道路运送货物，比如运送油品，而经过每条边的载货量不得超过这条边的x_ij值，也就是说用x_ij值来衡量连接i点和j点的管道容量。设每条通路赋值为1/2，从源点（出发地）流向汇点（目的地）的总流量就是2。

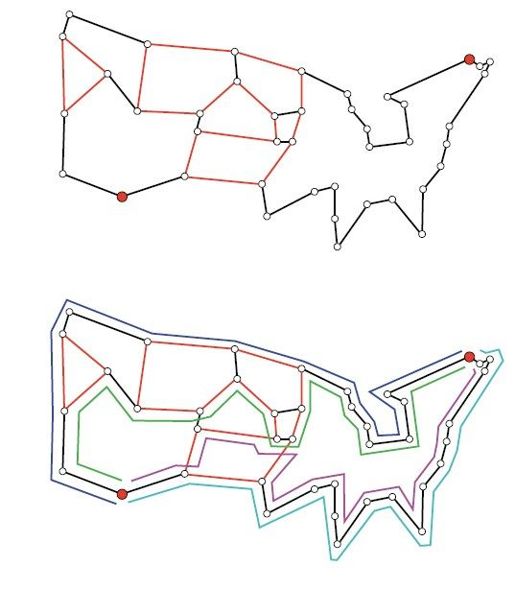
图6-13　Phoenix和Montpelier之间的4条通路

“流”的对偶概念是“割”。割就是一组边，假如在图中去除这些边，图就会变成两个互不相交的独立子图，其中一个子图包含源点，另一个子图则包含汇点，因此一个割把顶点分成两个集合。割包含的各边的容量之和是最大流量的一个上界，因为在运输油品途中，必然会在某时某处离开一个子图，到达另一个子图。在42座城市的例题中，我们可以把一端是Phoenix的所有边取作一个割，它的容量是2，与之前得到的流量相等。这并不是巧合，而是关于流和割的核心定理——最大流最小割定理。

最大流最小割定理是一个具有“强对偶性”的结论，内容是说，对于任意一个图，在图中任意选定源点（source）和汇点（destination），则流的最大值等于割的最小容量。由此可进一步推出，如果一个标准的多项式时间算法能计算最大流，那么它也能计算最小割。

注意，由割产生的两个子图中，有一个子图对应的子回路不等式取值恰好等于割的容量。又由于从Phoenix到Montpelier的流量为2，可以推知，任取一个只包含这两座城市之一的集合，它对应的子回路不等式都已经得到满足。依次把汇点（目的地）换成剩下的40座城市，如法炮制，便可证明，所有的子回路不等式均已得到满足。²

^{2. 集合S与其补集有相同的子回路不等式，S的补集由所有不在S中的顶点构成。因此，我们可以假定Phoenix属于集合S。}

总而言之，我们解决子回路分离问题的一般方法如下：首先选择一个源点，依次以其他顶点为汇点，计算出最大流，也就是求解n-1道最大流问题。如果计算发现所有的最大流量都是2，那么所有子回路不等式就都已经得到满足；反之，只要有任何一个结果小于2，则对应的最小割就不能满足某个子回路不等式。³听起来求解过程似乎耗时很长，但实际上完全可以实现很快的执行速度。

^{3. 流量问题是网络理论的基础，自冷战时期以来，网络理论一直在持续发展。欲知详情，可参考《网络流》一书（R. Ahuja, T. Magnanti, J. Orlin. Network Flows. 1983. Prentice Hall, Englewood Cliffs, New Jersey.）。}

6.3.2 梳子分离问题

子回路消去约束怎么样？没问题，已经搞定了。那么梳子不等式呢？不是太顺利。目前我们还没有找到合适的多项式时间算法，保证能够发现给定解不满足的梳子不等式。我们也没有把梳子分离问题归入NP完全问题的复杂度类，它的地位还没有定论。该问题悬而未决，而又亟需解决，换言之，它是个重要的研究课题。

虽然梳子分离问题尚未解决，但这不代表计算时就完全不考虑梳子。如果子回路消去约束条件不能改进线性规划最优解的界，计算机程序别无他法，必须找出有用的梳子，为此只能不择手段，使出浑身解数。程序做到了，使用的方法是试探策略，能够实现延长梳柄、缩减梳齿、切分集合等诸多操作。当然可能会遇到复杂混乱的情形，但其实在初始阶段很容易发现不满足的梳子结构。事实上，梳子不等式的结构表明，我们在寻找可能的梳齿时，应当观察现有线性规划解，考虑边界交叉次数取值接近2的集合。这样的集合其实有现成的，它们形如S={i, j}，这里i和j是解里满足x_ij=1的值，也就是图里黑色各边的一对顶点。因此，我们解决这一问题时，第一步可以在图中删掉所有黑色边，考察剩下的红色独立子图。如果这些黑色边与其中一个子图边界的交叉次数为奇数，就确定了一处不满足梳子不等式的结构。求解过程如图6-14所示，这里我们在子回路线性规划的松弛解中找到了两个可能有用的梳子不等式，并在下面两幅图里标明了梳子结构。在计算时，我们选择了左下图中有3个梳齿的梳子。

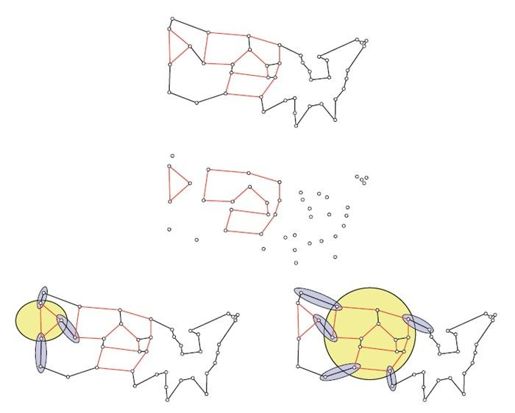
图6-14　以红色独立子图为梳柄的两个梳子结构

有好几种方法都可以用来寻找以单边为梳齿的梳子结构。除了上面介绍的现成捷径之外，也有一些更精巧的启发式算法，还有一种具有多项式运行时间的恰当分离方法。这些方法都很成功。研究者也发扬正宗的算法工程风格，充分利用试探算法寻找一般性的梳子。他们的核心思想是，先把城市构成的簇换成单个顶点，得到收缩图，然后再在其中搜寻以单边为梳齿的梳子。找到梳子以后，可以再反向展开，扩充为原图中一般性的梳子结构。这里的技巧在于簇的创造性选择，通常要借助一定方法，在线性规划解中搜索边界取值接近2的集合。在计算42座城市的TSP题目时，最后给出那把有3个梳齿的梳子的求解方法正是属于这一类启发式收缩聚类算法。

6.3.3 不自交的线性规划解

表面上，探索梳子分离算法的任务是没人想干的脏活累活，但实际上，这方面的研究会从其他各研究领域借鉴方法和结构，因此有可能发展成为非常有趣的数学研究。Lisa Fleischer和Éva Tardos在康奈尔大学的研究工作就是出色的例证，研究时间是20世纪90年代末期。¹对算法工程的紧迫需求涌现自计算方面的研究，主导了她们所处学术领域的研究方向。她们没有随大流研究试探风格的启发式算法，而是经过冷静思考，得出了优美精确的理论结果。这也是针对一般性梳子结构的第一个准确结果。

^{1. Fleischer, L., é. Tardos. 1999. Math. Oper. Res. 24, 130–148.}

Fleischer-Tardos研究的主旨是把重点放在满足特定条件的线性规划解上：这类解可以画成各边互不相交的图，例如之前看到的环游美国42座城市路线以及图6-15的1000座城市周游路线。这样的限制条件很有用。几何形式的TSP题目多数都有完全或近乎不自交的线性规划解。图论里有些工具虽然不能用在一般情形下，却适用于此类情况。她们通过分析，给出了一种分离算法，其运行时间为多项式时间。不过这种算法得到的梳子究竟质量如何，我们不能妄下结论。

图6-15　子回路线性规划的松弛解，题目包含1000座城市

已经知道，每条回路与k齿梳子的边界至少相交3k+1次。另外，如果线性规划解满足所有子回路消去约束条件，相应的相交次数取值就至少为3k次，也就是说梳子不等式即便得不到满足，最多也只会相差1。现在给定一个不自交的线性规划解，只要存在一个梳子结构使二者相交次数取值为3k，就可以保证Fleischer-Tardos算法必定能给出一个这样的梳子结构。然而，如果梳子不等式的违背程度不到1，而是1-δ，其中δ是一个很小的数，那么该算法未必能保证找到这样的梳子。因此，该算法令人喜忧参半。一方面，它能找到违背不等式程度最大的梳子，这是件好事；可是另一方面，它找不到梳子时，有可能依然存在许多梳子结构使不等式不成立，从务实的角度来看，漏掉这些梳子当然是件坏事。

能够完全解决不自交线性规划解的梳子分离问题的多项式时间算法，应该如何构造？这一研究问题依然有待解决。它的答案不但将成为重大的理论成就，而且很可能直接影响TSP的实际计算。英国兰卡斯特大学的Adam Letchford对此作了探究。他采用了Fleischer-Tardos研究的思想，只不过改变了思路，自下而上建立起一类新的约束条件，得到了不自交情形下的多项式时间分离算法。²Letchford的一系列约束条件包括梳子结构和许多其他结构，统称为多米诺奇偶性不等式（domino-parity inequality）。

^{2. Letchford, A. L. 2000. Math. Oper. Res. 25, 443–454.}

图6-16　Lisa Fleischer（左）、Éva Tardos（中）和Adam Letchford（右）

“许多其他结构”听起来好像不错，但是它的实际后果并不清晰。根据已有的海量计算研究，我们知道，梳子不等式的力量非常强大，但是Letchford的多项式时间算法给出的约束条件更为一般，有时候虽然是当前解不满足的梳子不等式，但并不是小平面定义不等式。几年后，Sylvia Boyd、Sally Cockburn和Danielle Vella组成的加拿大研究小组解决了这个问题。他们把人工计算和计算机程序实现结合起来，证明Letchford算法用在中等规模的测试题目上非常高效，结果令人印象深刻。³在Daniel Espinoza和Marcos Goycoolea的领导下，佐治亚理工学院的研究小组紧随其后，完成了一项大型计算研究，全面实现了该算法的自动化。⁴这项研究成果成为了Concorde程序的重要新增模块，大大提高了TSP求解速度，最终解决了85 900座城市的题目，创下TSP实战领域的纪录。

^{3. Boyd, S., S. Cockburn, D. Vella. 2007. Math. Program. 110, 501–519.}

^{4. Cook,W., D. G. Espinoza, M. Goycoolea. 2007. INFORMS J. Comp. 19, 356–365.}