9.5 非计算机不可吗
尼尔·斯蒂芬森(Neil Stephenson)在科幻小说《飞越修道院》(Anathem)中描述了一台神奇的外星机器,它能解决“偷懒的佩里格林”(Lazy Peregrin)问题——这个名字是他虚构的,本质就是旅行商问题。
“说的就是那道题,一个漫游者需要拜访好多个数学圈,那些数学圈四处散落在地图上。”
“没错,问题要求找出经过所有目的地的最短路线。”
“我大概明白了,”我说,“可以列一张表,穷举出所有可能路线。”
“但那样永远也算不完的,”奥若罗说,“在葛罗德圣人的机器里,你可以推广这种情况,设计某种一般化模型,配置机器,使它实际上同时检验所有可能路线。”
“葛罗德圣人的机器”有魔力,但现实世界里,同时检验所有路线的实体设备也已针对TSP构想出来,甚至存在某些测试实例。别忘了,图灵风格的计算绝对不是解决旅行商问题的唯一手段。
9.5.1 DNA计算TSP
如何制作“葛罗德圣人的机器”?1994年,美国南加州大学教授Leonard Adleman提出了一种生物思路1。Adleman是一位曾获大奖的计算机科学家,“RSA密码系统”中的“A”指的就是他的鼎鼎大名。他的TSP解题装置在分子层面运作,力图利用极少量DNA存放无数信息。
1. Adleman, L. M. 1994. Science 266, 1021–1024.
Adleman解决的题目是TSP的变形,属于哈密顿路径问题。输入为一个图,目标是找到一条路径,起始和终止顶点均已指定,要求该路径周游所有顶点,但不考虑旅行成本问题。他在实验中采用了一道包含7座城市的例题,如图9-4所示,从城市0出发,到城市6结束。在这个例子里,大多数边都类似于道路的单行线,哈密顿路径必须遵从箭头所示方向。只有顶点1和2之间、顶点2和3之间的两条边允许双向通行,其他边则都只允许单向通行。
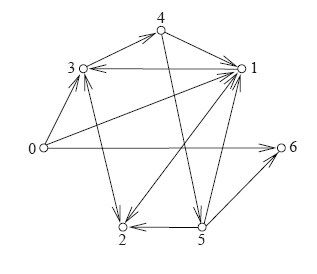
图9-4 有向哈密顿路径问题
针对该问题,Adleman发明了一种分子编码,赋给每个顶点一个随机的20位DNA字母串。例如,赋给顶点2的DNA字母串为
TATCGGATCG|gtatatccga
而顶点3则为
GCTATTCGAG|cttaaagcta
如上所示,20位字母串的顶点标签可以分成两组,视为相连的两个10位字母串标签,第一个标签全由大写字母组成,第二个则全是小写字母。这样一来,要表示从顶点a指向顶点b的边,就可以把a的后半标签和b的前半标签组合成一个字母串。例如,从顶点2到顶点3的边就是
gtatatccga|GCTATTCGAG
两段字母串分别取自顶点2的后一组和顶点3的前一组。这条规则只有两种例外情形,就是边包含起始顶点0和终止顶点6的时候。此时不再只用一半的10位字母串,而是使用整条20位字母串标签。如果一条边允许双向通行,则将它拆分成两条单向边,分别指向一个方向。
下面进入Adleman解法的第二步,给出一种能把各边连成一条路径的机制。除了起点0和终点6,对于其他每个顶点,写出字母串标签的互补DNA序列。在按照一致的方向连接两条边的时候,这样的序列起到“夹板”的作用。以顶点3为例,它的互补序列可以连接边(2, 3)和边(3, 4),因为该序列的前半段与边(2, 3)的后半段互补,而序列的后半段与边(3, 4)的前半段互补。
在Adleman领导的实际实验中,研究者在实验室制备了分别与边和“夹板”对应的DNA链的多份副本,并将它们混合起来。经过七天的缜密工作,他们最终发现了一条得到完整哈密顿路径的双链。
9.5.2 细菌
Adleman的实验需要有位科学狂人在实验室里辛辛苦苦工作一个星期,而处理DNA原本就是活的生物的拿手好戏,所以改用其他生物替人干活的主意值得一试。由一群本科生组成的研究小组就实现了这个点子,在细菌体内构建合适的DNA序列,成功解决了哈密顿路径问题的一道小例题1。研究小组的成员来自美国大卫森学院、约翰逊 C.史密斯大学、西密苏里州立大学和北卡罗来纳中央大学四所院校。
1. Baumgardner, J. et al. 2009. J. Biol. Eng. 3, 11.
当然,使用细菌计算机自有其难处:既然对应于路径的DNA包埋在活体内部,研究者要如何发现并识别它呢?上述研究小组的答案是,利用荧光性质,迫使体内DNA确为路径的细菌菌落发光。他们用一道三座城市的题目演示了荧光方法。当两条有方向的边在哈密顿路径里相接时,红色荧光和绿色荧光叠加,得到发黄光的细菌菌落。实验结果如图9-5所示,展示了这一思想。左图中,DNA链的初始顺序构成了哈密顿路径,细菌生长之后便出现了许多黄色菌落;右图中,DNA链的初始顺序是错误的,但经过一系列突变,有一定数目的菌落“变节”了,显示出不该属于它们的黄色。
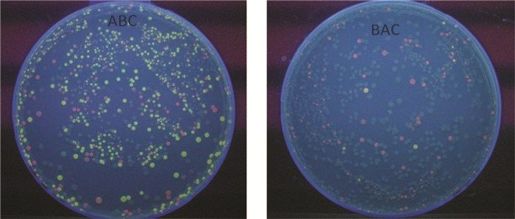
图9-5 哈密顿路径的细菌计算实验,Todd Eckdahl供图
好吧,三座城市确实太少了,几乎算不上TSP。不过毕竟总要从简单的例子讲起,而且这里的重点在于思想很巧妙。细菌培养时,数目会呈指数增加,这一特点或许可以用在规模更大的计算中,届时需要使用更加精细的方法来筛选整理得到的菌落。
9.5.3 变形虫计算
从低等的细菌走向食物链的上游,接下来登场的是单细胞的变形虫。一个来自日本的研究团队创立了使用变形虫解决TSP题目的通用做法——变形虫计算可解决一般的TSP题目,而不仅限于哈密顿路径问题。1该变形虫计算机的核心部件如图9-6所示,左侧是一只变形虫,右侧是一枚具有星形开口的塑料构件。将变形虫放在构件中,它会逐渐变化自身形状,完全填充构件中心的星形空间。因为变形虫会避开光源,所以可在构件的每条星形放射状分支内打开或关闭光源,借此引导变形过程。要点是变形虫有能力响应变化环境并调整至最优外形,而研究者恰要利用这一能力。
1. Aono, M., et al. 2009. New Generation Comp. 27, 129–157.

图9-6 单细胞变形虫和星形围栏构件,青野真士供图
四座城市TSP的解题程序在变形虫计算机上的实现如图9-7所示。这里用到的星状结构具有16个放射状分支,每座城市都由4个分支表示。城市A对应的分支标记为A1、A2、A3、A4,数字表示城市A在总路线中所处的位次,如果变形虫选择A2,则A就是路线中第二座城市。实验开始1小时14分钟之后,变形虫开始将一只伪足探入A4分支。这时,计算机程序在A1、A2、A3处打开光源,以保证满足城市A只能在路线中出现一次的规则。同理,B4、C4、D4处的光源也同时开启,以保证满足只能有一座城市处于路线中第四位的规则。不过,上述光照步骤在变形过程中不会始终严格维持,这是为了在短暂关闭光源的时候,让变形虫有机会重新选择其他城市作为路线的第四位城市。为了引导变形虫获取较短路线,选定A4后,距离A较远的城市的1、3位分支会开始闪烁照明,阻碍变形虫选择这些分支。最终,变形虫到达稳定状态,给出的解对应于路线D-C-B-A。
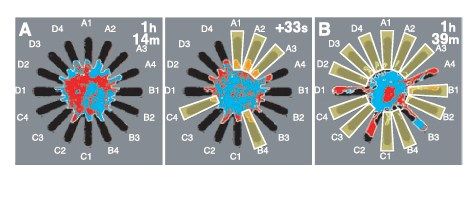
图9-7 变形虫求解4座城市的TSP题目(青野真士供图)
和细菌求解的例子差不多,这里只有四座城市,没有真正的计算难度可言。这项研究的最重要之处在于,研究者发明了一种由生物构成的新型可工作计算机。
9.5.4 光学
“葛罗德圣人的机器”还有一种基于光学的方案,用于求解哈密顿路径问题。2007年,这种解法在互联网上一鸣惊人。1它的思路是构造图对应的物理装置,光纤对应边,延时装置对应顶点。机器运行时,光到达一个顶点,经过固定的延迟时间之后分散成多束光线,分别沿着自该顶点引出的各边传播。延迟装置用来提供特征信号,用以标志光线已传过相应顶点。令D等于每个顶点恰经过一次时整条路线的延迟总时长。解决哈密顿路径问题时,我们从起始顶点发射光线,检验光线是否在D个单位时间之后到达终止顶点。
1. Haist, T.,W. Osten. 2007. Optics Express 15, 10473–10482.
表面上看,这种光学解题机器解决n座城市的问题时,需要的步骤数目正比于图的顶点数目。它之所以一举成名,正是因为人们看中了这一点。然而,罗马尼亚计算机科学家Mihai Oltean经过仔细分析得出结论,选择延迟时间长度的时候,若想给出可分辨的特征信号,D必须至少为2n个单位时间。2目前,接收时间差如果小于10-12秒,示波器就无法区分,因此解题时间至少是2n×10-12秒,按照指数速率增长。幸好,数字还是很小,中等规模的题目也能很快解决。
2. Oltean, M. 2008. Natural Comp. 7, 57–70. Oltean的研究也出现在2006年的一份会议论文集中,先于Haist和Osten的研究。
据Oltean估测,如果图具有33个顶点,那么一秒钟就够了,还不错。不过同样据他计算,实现该例的延时装置需要的线路长达8×1011米。此外,要解决一道包含几百个顶点的题目,需要的光子数目比太阳每年输出的光子数目还多。这下可不好办了。
9.5.5 量子计算机
无论是基于DNA、细菌、变形虫还是光学原理,上述TSP解题程序虽然都有完全一步到位的优点,但是也都离不开随城市数目增加而呈指数增长的资源。要制造货真价实的“葛罗德圣人的机器”,或许需要抛开生物和古典物理,另谋出路。事实上,我们发现一种更有可能成功的思路要利用量子物理学特性。第一个提出把量子物理用在计算设备中的人是Richard Feynman。
量子计算设备最为基本的组成部分是量子位(qubit)。传统计算机使用0/1二进制位表示信息,量子位与传统二进制位类似,但很特别。它能够存放值0,也能存放值1,还能同时存放0和1两个值。根据量子力学的神奇特性,如果有100个量子位,那么它们合起来就能同时编码2100种可能性,因此确实有可能实现真正的“一步到位”,一次检验所有TSP路线。
世界各地的研究小组都在孜孜不倦地奋战。他们希望能克服物理和工程方面的困难,从而开发出能正常运转的量子计算机。根据Peter Shor的知名结果,这样的计算机将给出整数因子分解问题的快速解法。不过,如果认为数目众多的量子位就能保证轻松求解旅行商问题,那你就错了。诚然,一百万个量子位足以编码周游1000座城市的每条路线,问题出在物理学上。虽然所有路线都能同时表示,但是真正考察所有量子位状态的时候,却只剩下一条路线,其他路线全都消失得无影无踪。既然有这么糟糕的现象,我们怎么可能让机器选出最优路线呢?问得好,眼下人们确实不清楚是否可能。
Scott Aaronson在《科学美国人》上发表了一篇文章,对此作了讨论,并描述了量子计算的可能局限。1关于NP完全问题的多项式时间量子算法,他针对其难度写出了如下评论:
1. Aaronson, S. 2008. Sci. Am., March, 62–69.
假如存在这样的算法,那么算法必然会以前所未见的方式利用问题的结构,而同类问题的传统高效算法也是如此,两种利用方式大致相同。仅凭量子的神奇特性本身,将无法获得成功。
量子计算机具有迷人的神奇性能,类似图灵机的传统计算机难以望其项背。但是它究竟能否派上用场,能否显著增强给旅行商指路的能力,目前依然没有定论。
9.5.6 闭合类时曲线
Aaronson的文章还讨论了几种猎奇的计算模型,其中之一是我的最爱——时间旅行解题程序。原理很简单。在稳定可靠的计算机上开始运行Concorde程序,并设置程序将很久之后找到的解传回到当前时刻。这样一来,一眨眼就能完成,但是读者自然要问:我们从这台时间机器上接收到解之后,能否直接关掉计算机?如果立刻关机,那么Concorde是怎么找到那个解的?
有些人认真琢磨这些思想,想到“闭合类时曲线”的概念,即路径穿越时间和空间之后首尾相接,构成闭合的环路。1如果存在这样的环,那么旅行商就会在曲线中途被追上,我们或许就能在返程途中得到解。
1. Deutsch, D. 1991. Phys. Rev. D 44, 3197–3217.
9.5.7 绳子和钉子
回到现实世界,让我们脚踏实地,别忘了Dantzig、Fulkerson和Johnson使用的那台实体装置,还有20世纪初期货真价实的旅行商背后的助手团队。他们使用的都是钉绳法,即用图钉在地图上标出目的城市,再用一条绳子勾勒出可能的路线。绷紧绳子便可以测量路线长度,所以这种装置比纯手工计算更快,又比穿越时空的量子计算机更容易搭建,直至今日仍是最实用的TSP实体辅助解题工具。
