2.3 维也纳—哈佛—普林斯顿

欧拉和哈密顿都曾研究路线，但是从国际象棋棋盘和正十二面体到上路奔波的旅行商之间却有天壤之别。对旅行商来说，可不是随便哪条路线都能满意。他们只想要总路程最短的那一条。

为了讨论实际旅行成本，我们要前往奥地利的维也纳，拜访Karl Menger，了解他的研究工作。在20世纪20年代，Menger最关心的研究题目包括一项：度量空间曲线长度的方法。 可能是在这项内容艰深的研究的启发下，1930年2月5日举办的一场学术讨论会上，Menger公布了一道与TSP密切相关的题目¹。

_{1. Menger (1931).}

我们用“邮递员问题”（messenger problem）一词表示这样一个问题（因为每位邮递员在实际工作中都会遇到这个问题，不过许多旅行者也会遇到）：给定有限数目的点，它们两两之间的距离已知，试求连接所有点的最短路线。

这道题也就是要找到一条周游所有点的路线，但不需要最终回到起点。所以只需要在终点和起点之间添加一个“虚城市”，就可以把通路两端连接起来，形成一条回路，从而转化为TSP路线。可以设“虚城市”和任意一座真实的城市之间的路费都为零，这样一来，虽然增加了一座城市，但并不会干扰我们选择路线的起点和终点。

在维也纳数学研讨会的出版文献资料中，留下了关于Menger邮递员问题的德语文献记录。这一问题的发表显然具有重要的历史地位，但是美国的TSP研究热潮似乎并不直接来源于此，而应该归功于哈佛大学的优秀数学家Hassler Whitney。Dantzig、Fulkerson和Johnson的经典论文里提到了Whitney的讲座。²

_{2. Dantzig, Fulkerson, Johnson (1954).}

哥伦比亚大学的Merril Flood多次介绍旅行商问题，在激发相关研究兴趣方面功不可没。早在1937年，他便努力求解校车路线的近优解。Flood和普林斯顿大学的Albert. W. Tucker都回忆说，他们最早得知这道题是在1934年，当时Hassler Whitney在普林斯顿大学做了一次学术报告（尽管近期向Whitney本人求证时，他似乎对此全无印象）。

Merril Flood在叙述TSP的研究历史时，也把功劳归于Whitney的讲座。在1956年的一篇论文里，他写道：“该问题于1934年由Hassler Whitney在普林斯顿大学的一场学术报告上提出。”³很久之后，到了1984年，Flood在接受Tucker的访谈时，仍然用“Whitney的48州问题”代指TSP。⁴

_{3. Flood, M. M. 1956. Operations Research 4, 61–75.}

_{4. Flood, M. M. 1984. The Princeton Mathematics Community in the 1930s, Transcript Number 11 (PMC11). Princeton University.}

人们会很自然地猜想，在Menger的维也纳研讨会和Whitney的普林斯顿报告会之间，可能存在某种联系。Alexander Schrijver发现了证据。他指出，在1930年到1931学年间，Menger曾到Whitney所在的哈佛大学访问了一学期⁵，因此他们两人曾经见面。然而，至于他们在交流中是否直接提到了旅行商问题（邮递员问题），目前仍不得而知。

_{5. Schrijver（2003）一文中详细地记录了Menger的具体工作。}

同样，Whitney当年在普林斯顿大学是否真的讨论过TSP，也依然没有定论。很遗憾，普林斯顿大学并未保留20世纪30年代的数学系学术研讨会记录。不过，哈佛大学普西图书馆却有另外一些档案。这里收藏了Whitney的论文，文档总体积达到0.1立方米。其中有一批手写的笔记写于1930年后不久，似乎是Whitney为学术研讨会做准备时写的。笔记中介绍了图论，摘录一段如下。

下面是一个难度更大的类似问题：我们能否在一个图中找出一条简单闭合曲线，要求它恰好经过每个顶点一次？该问题对应另一个问题，即，给定一组国家，是否可能以某种方式周游列国，从而恰好到达每个国家一次？

把每个国家看作一个顶点，若两个国家之间有公共边界，就在对应的两个顶点之间连一条边，便得到了第一个问题中的图。第二个问题中周游列国的路线就是图里的一条哈密顿回路。用这样的例子来描述哈密顿回路问题，其实并不是无心之选，而且这道题距离真正的TSP显然只有一步之遥。

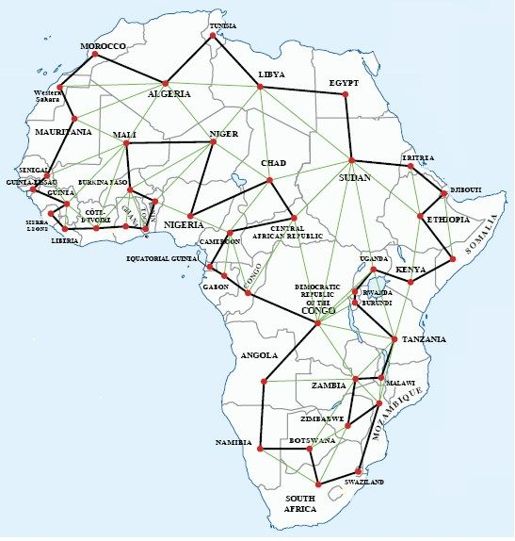
图2-18　周游非洲的哈密顿回路

惠特尼例题具有地理背景，与Flood回忆起的环游美国48州问题彼此吻合。确实，惠特尼用来说明哈密顿回路的例子很可能就是美国TSP研究的源头。正如Alan Hoffman和Philip Wolfe评价的那样，惠特尼把旅行商介绍给数学界的过程中，角色“也许相当于门格派来的邮递员”⁶。

_{6. Hoffman and Wolfe (1985).}