2.2 欧拉和哈密顿

那个时代，在数学的王国里，数学家正在为飞速发展的自然科学打下根基，研究工作忙得不可开交，无暇顾及旅行商、巡回律师和牧师面临的难题。然而，数学界的两大领军人物确实曾经探索过旅行商问题的部分领域。如今，我们把他们两人推崇为TSP研究的开山鼻祖。这是他们应得的评价。

2.2.1 图论与哥尼斯堡七桥问题

有关路线问题的早期数学文献中，最重要的一篇论文来自伟大的莱昂哈德·欧拉（Leonhard Euler）。The Euler Archive（欧拉档案网站）引用了历史学家Clifford Truesdell的一句评价：“若能列出18世纪数学、物理学、工程学、天文学、航海学方面的所有论文，则其中欧拉的作品将占到整整四分之一。”欧拉是历史上最多产的数学家。他的研究范围很广泛，其中有一道难题曾经长期困扰哥尼斯堡的居民。

这座城市旧称哥尼斯堡，当时属于东普鲁士，如今已改名为加里宁格勒。图2-8是当地的卫星图像。可以看到，普莱格尔河流经哥尼斯堡，形成了错综复杂的水路。中间的长方形岛屿是克奈芳福岛（Kneiphof），河道在岛的两侧分流而过；东侧是较大的朗兹岛（Lomse），两岛隔河相望；河流北岸的部分为老城区（Altstadt），南侧则是郊区（Vorstadt）。¹

_{1. Gribkovskaia, I., O. Halskau, G. Laport. 2007. Networks 49, 199–203.}

图2-8　哥尼斯堡（今加里宁格勒）和普莱格尔河（今普列戈利亚河），TerraServer.com，2011年

在欧拉那个年代，普莱格尔河上一共架有七座桥梁：克奈芳福岛和老城区之间有绿桥（Green）和下桥（Köttel）两座桥梁，克奈芳福岛和郊区之间也有商人桥（Krämer）和铁匠桥（Schmiede）两座桥梁，克奈芳福岛和朗兹岛之间是蜜桥（Honey），朗兹岛和老城区之间是高桥（High），朗兹岛和郊区之间则由木桥（Wood）连接。哥尼斯堡的居民都是好市民，喜欢在城里散步，通过绿桥、下桥、商人桥、铁匠桥、蜜桥、高桥³、木桥这七座桥往返于普莱格尔河两岸。据说，当地流传着一道多年未解的难题：如何在一场散步中走过全城各地区，七座桥中的每一座都必须恰好走过一次？

_{3. 原文误作Lomse，实际应为High。——译者注}

这就是哥尼斯堡七桥问题（Königsberg problem）。1735年8月26日，欧拉向圣彼得堡科学院提交了一篇论文，发表了对该问题的看法。⁴为了抓住问题的本质，他按照经典的数学思想，只把必要的信息提取出来，从而解决了问题，也开辟出了一个新的数学分支。这个新分支就是图论（graph theory）。⁵

_{4. Euler, E. 1741. Comm. academiae scientiarum Petropolitanae 8, 128–140.}

_{5. Biggs等人将欧拉的论文译成了英文，并对其影响做了详细的学术论述，参见*Graph Theory 一书。}

首先，欧拉抛开这个问题的具体背景，将城镇、河流、桥梁抽象出来，画成示意图，如图2-9所示。（图2-9取自欧拉原始论文副本的扫描件，图片经过处理。）他分别用大写字母A、B、C、D表示哥尼斯堡城的4个区域，又用小写字母a～g表示普莱格尔河上的七座桥。这11个字母足以描述城里的任何一条路线，比如一条路线可以描述为：从A地经过c桥到达C地，再从C地经过g桥到达D地，从D地经过f桥到达B地，最后从B地经过b桥回到A地。这条路线也可以简记为AcCgDfBbA。欧拉的论证完全建立在这种表示的基础上。他把路线视为字符串，而不是行人的实际散步路线。

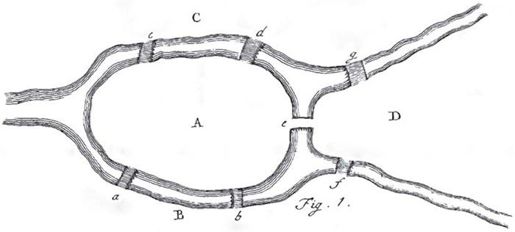
图2-9　欧拉简化后的哥尼斯堡七桥图

在这道题目里，A、B、C、D 4个区域的面积与论证完全无关，因此可以把它们都抽象成一点，而把a到g的桥梁抽象成连接两点的线，从而把题目形象化，画成一张更简单的图，如图2-10所示。图的含义不受点和线的形状、大小的影响，只和线的连接方式有关。这就是图论中的图（graph）。其中，点称为顶点（vertex），线称为边（edge），每条边两端的点是边的两个端点（end）。

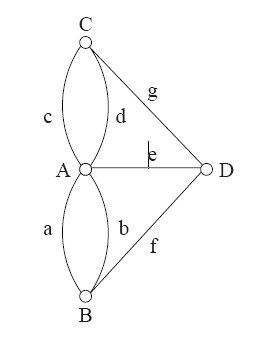
图2-10　哥尼斯堡七桥问题的图表示

经过简化以后，居民在哥尼斯堡城散步便可以理解成沿着边在图的各顶点之间移动。从B到D的一条散步路线可以写成BaAcCgDeAbBfD。在这条路线经过的边中，与顶点B相连的边有3条，分别是a、b、f；与顶点A相连的边有4条，分别是a、c、e、b；与顶点C相连的边有2条，分别是c、g；与顶点D相连的边有3条，分别是g、e、f。经过各顶点的边数依次为奇—偶—偶—奇，这样的排列并非出于偶然。欧拉发现了最关键的一点：若散步的起点和终点不同，则路线中，分别以起点或终点为端点的边都是奇数条，以途中任何一点为端点的边则都是偶数条；此外，如果散步路线是闭合的，也就是说起点和终点是同一点，那么以任何一个顶点为端点的边都有偶数条。综上可见，要么所有顶点都是“偶点”，要么恰好有2个顶点是“奇点”。

对哥尼斯堡城的居民们来说，这真是个坏消息。七桥问题的图里，4个顶点都与奇数条边相连，都是“奇点”，所以不可能在一次散步中经过每座桥恰好一次。欧拉的论证非常简短，却结束了哥尼斯堡问题的所有争论。

2.2.2 骑士周游问题

几年后，欧拉又写了一篇论文，再次讨论周游路线难题。¹这次的题目来自国际象棋，称为骑士周游问题（knight's tour problem）。问题是：能否按照一定顺序移动骑士，让骑士从棋盘上的某一格出发，走遍整张棋盘，落在每一格上恰好一次，最后回到出发的格子？²欧拉的解法如图2-11所示，每格的数字表示骑士出发后第几步到达这一格。

_{1. Euler, L. 1766. Mémoires de l'Academie Royale des Sciences et Belles Lettres, Année 1759, Berlin. 310–337.}

_{2. 国际象棋的标准棋盘有8行8列，骑士相当于中国象棋中的马，走“日”字格，即每移动一步时，或者横走两格竖走一格，或者横走一格竖走两格。——译者注}

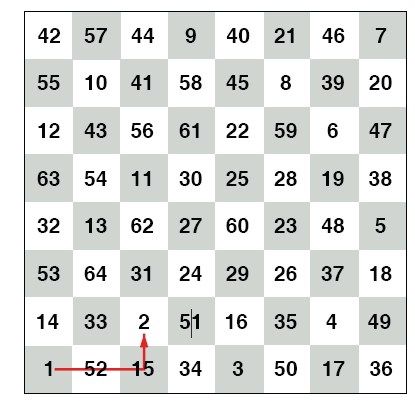
图2-11　欧拉为骑士周游问题给出的解法

欧拉对骑士周游这种想法很感兴趣，对于棋盘不是标准尺寸的情形也给出了解法。这些问题可以用图清楚地表示出来。我们用顶点表示棋盘上的格子，若骑士只用一步就可以从某格走到另一格，则在相应的两点间连一条边。骑士周游路线是指一条闭合路线，它到达每个顶点刚好一次。（在哥尼斯堡七桥问题里，所求的散步路线经过每条边刚好一次，请注意这两道题目的相似之处。）如此，可以将整张标准棋盘转化为图2-12所示的图，其中红色路线是欧拉的解答。

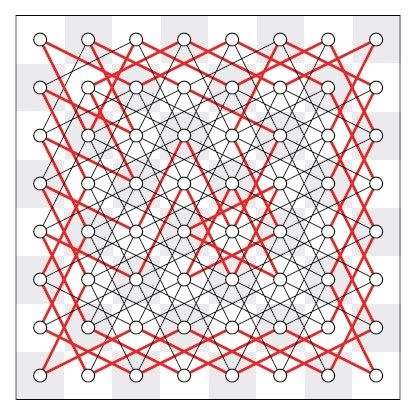
图2-12　用图表示的骑士周游路线

2.2.3 Icosian图

威廉·卢云·哈密顿爵士（Sir Wiliam Rowan Hamilton）是一位爱尔兰数学家。在欧拉之后一个世纪，哈密顿同样对某道与图相关的路线问题产生了兴趣。他研究了经过正十二面体全部20个顶点的路线，把正十二面体抽象为图2-13所示的图形，称之为Icosian，意即“有20条边的图形”。图上的线段代表正二十面体的棱，而标有字母的小圆圈代表顶点。

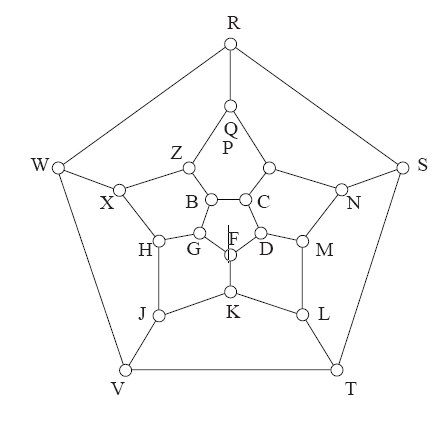
图2-13　Icosian图

图2-14　哈密顿纪念邮票（爱尔兰邮局于2005年发行，哈密顿画像由爱尔兰皇家科学院提供）

哈密顿和欧拉一样，要求路线沿着Icosian图的边前进，依次经过各个顶点。但是哈密顿的做法非常有趣。他引入了一种代数系统来考虑图上的路线，与他对四元数的定义式在本质上高度一致。1856年，他在写给朋友John T. Graves的一封正式信函中描述了他的思路。¹

_{1. Hamilton, W. R. 1856. In: H. Halberstam, R. E. Ingram, eds. The Mathematical Papers of Sir William Rowan Hamilton, Volume III. Cambridge University Press, Cambridge, UK. 612–624.}

我将延续此前寄出的信里的做法，设三个符号ι、κ、λ满足下面的4个等式：

ι²=1，κ³=1，λ⁵=1，λ=ικ

首先，我要举一两个例子来证明，这些符号在以上定义下，具有奇妙而确定的性质，从而足以成为合理的计算工具。对于它们得出的符号化的计算结果，我做了大量检验。在我看来，每一个结果都可以解读为古典几何学的某个多面体中连接各面或者各顶点的一条路线。这种理解方式很简单，而且往往很有趣。

这3个符号对应Icosian里的3种操作。符号之间做乘法相当于依次进行各个操作。²哈密顿利用这些符号进行计算，表明了无论从五个顶点中的哪一个出发，都有可能完成一条周游Icosian的路线。哈密顿非常喜欢Icosian图的结构，在信的末尾还向Graves介绍了一个在Icosian图上玩的游戏。

_{2. ι对应的操作就是在一条边上反转路线，κ对应在顶点处顺时针旋转到下一条边，λ对应在顶点处左转。因此，以连续做5次λ操作为例，实际就是在图中走出一条五边形路线，最后将回到原点，这就解释了为什么哈密顿定义λ⁵=1。}

我发现有些年轻人很喜欢玩一个新的数学游戏。这个游戏来自Icosian图，一个玩家选取任意连续5个点，比如abcde或者abcde'，插上5枚大头针，然后另一个玩家按照一条连续环状路线，再依次插入15根大头针，目的是到达剩下的每一个点，而且最后一枚大头针应当与对手插入的第一枚相邻。按照我在这封信里叙述的理论，符合条件的路线总是存在的。

后来，英国的一个玩具经销商推出了基于这个游戏的两款产品。第一款叫做“环游世界”游戏（Icosian Game），由一块木制棋盘和一些用来标注到过哪些点的象牙棋子组成。第二款则是一个手持玩具，名为“旅行者的十二面体——环游世界之旅”（Traveller's Dodecahedron: A Voyage Round the World），形状为压扁的十二面体，配有一些用来标记点的棋子，还有一条细绳用来勾勒路线。³

图2-15　“环游世界”游戏（左）和“旅行者的十二面体”游戏（右）

（© 2009 Hordern-Dalgety Collection, puzzlemuseum.com）

_{3. 哈密顿游戏的两幅插图（图2-15和图2-16）由James Dalgety提供。他创办的智力玩具博物馆（Puzzle Museum）收集了各年代的智力玩具和游戏，藏品引人入胜。}

虽然哈密顿热情高涨，他的游戏在市场上却一败涂地。你若亲自玩上几个回合，很快就会发现问题出在哪儿——Icosian图的路线实在太好找了。哈密顿极力为自己的游戏辩护，说他本人觉得玩起来相当有难度。看来，同样一个游戏，对小孩子来说很容易，对爱尔兰最伟大的数学家来说反而很难。之所以会出现这种奇怪的状况，可能是因为哈密顿思考时总是从代数的观点出发。说不定他玩游戏的时候，并不是用眼睛寻找路线，而是在脑海中进行ι、κ、λ操作来算出结果。

不过可喜的是，到了20世纪，哈密顿的游戏改头换面，成功地打开了销路。1975年，James Dalgety推出了“蠹虫之困”游戏（Worried Woodworm）。玩法也是要求玩家在一个图里找出路线，但是这次的图比较特别，路线很难发现。图2-16就是游戏使用的木制地图板。玩家的主要目标是以左下角的小孔为起点，右上角的小孔为终点，找到一条遍历板上每个小孔的路线。

图2-16　“蠹虫之困”游戏（Worried Woodworm）

（© 2009 Hordern-Dalgety Collection, puzzlemuseum.com）

Dalgety还补充了“蠹虫之困”游戏的其他挑战题。最近在解决这些难题的过程中，Concorde代码也派上了用场。如今的“玩家”在寻找周游23个点的蠹虫路线时，可以借助先进的TSP求解程序和高效的计算机。毫无疑问，光明磊落的玩家心里一定对这种做法不以为然。

2.2.4 哈密顿回路

不论是在欧拉的棋盘上周游的骑士，还是玩哈密顿的游戏的小孩子，他们都在寻找图中的路线。但是对于一般情形的问题，结果又如何呢？并不是所有的图里都能找到一条周游顶点的路线。判断哪些图有这样的路线，哪些图没有，则是一道难题。当年在数学领域中，图论才刚刚开始寻求一席之地，哈密顿的鼎鼎大名让这道难题增色不少。正因为这段往事，他的名字在本节第一个登场。但是，不要因为我们冷落了欧拉而吓一跳。图论研究者暂时不用欧拉的名字，是为了把它留给另一类闭合路线，比如哥尼斯堡居民心驰神往的散步路线。因此，在一个图中，哈密顿回路（Hamiltonian circuit）就是经过所有顶点恰好一次的闭合路线，而欧拉回路（Eulerian walk）则是经过所有边恰好一次的闭合路线。¹这两种回路都是图论中的基本概念，虽然表面很相似，实际意义却天差地别。

_{1. Eulerian walk是欧拉通路，欧拉回路应该是Eulerian circuit或者Eulerian cycle。本书原文没有明确区分通路和回路的概念，但是提醒读者注意。严格说来，回路是起点与终点相同的通路，通路本身未必是闭合路线。——译者注}

要想判断一个图中是否存在哈密顿回路，是一个NP完全问题，复杂度与一般形式的TSP相当。然而对于欧拉回路的存在性，却存在一条简单的判定规则：图里可以有孤立顶点，不连接任何边，但除此之外，其他部分必须是连通的（connected），也就是说必须是连成一整片的，每个顶点都应该与偶数条边关联。

所以我们可以理解欧拉，却理解不了哈密顿。而且，年复一年，许多无畏的数学家提出了哈密顿回路的充分条件，可是他们的猜想最后都被推翻了。其中有一个例子非常著名，这就是P. G. Tait于19世纪80年代提出的猜想。当时，Alfred Kempe宣布证明了四色定理，得出结论说，至多只需要使用四种颜色，就可以给任意一张地图上色，使得任意两个有公共边界的相邻区域（国家或地区）都染成不同的颜色。这一发现令世人大为兴奋。Tait也受到了感染，并试图寻找另一种方式证明四种颜色就足够了。于是，他提出了一个猜想，认为在某一类图中一定存在哈密顿回路。

旅行路线和地图上色是如何联系起来的呢？把地图上每个区域的边界看作图的边，边界的交点看作图的顶点，你就明白了。生成的边界图里若存在一条哈密顿回路，则可以根据它来给地图染色。做法如图2-17所示，其中红色的边连成一条哈密顿回路。哈密顿回路不会自交，因此有内部和外部之分。位于回路内部的每条边都横穿内部区域，将其一分为二，从而可以只用两种颜色交替给内部区域染色，每经过一条边就换成另一种颜色即可；同理，回路外部的区域也可以只用另外两种颜色完成染色，最终就得到一幅四色地图。在图2-17中，内部区域使用深黄色和浅黄色染色，外部区域则用深蓝色和浅蓝色交替染色。

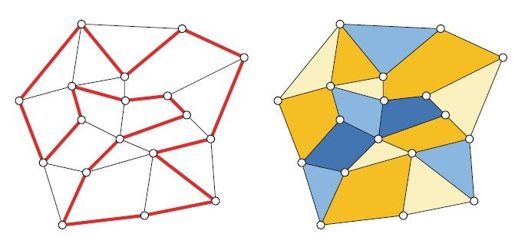
图2-17　通过哈密顿回路给地图染色

Tait知道，并非所有地图都存在沿着边界的哈密顿回路（美国本土地图就是一个现成的反例），但是可以通过一定的技巧，将四色问题的地图限定为边界图中每个顶点恰好连接3条边的情形，即3正则的（three-regular）。还可以进一步假定边界图是3连通的（three-connected），也就是说通过去掉一个或者两个顶点，可以把图分成两部分。Tait猜想，在这样的3正则、3连通的地图中，总是存在哈密顿回路。

William Tutte是伟大的图论专家，也是伟大的“布莱切利园”²密码破译专家。1946年，Tutte最终证明了Tait的猜想是错误的。这实在是非常遗憾，但是Kempe的四色证明早在1890年就被P. J. Heawood推翻了，相比之下，至少Tait的回路猜想坚持的时间更久。

_{2. “布莱切利园”（Bletchley Park）是二战期间英国政府情报部门进行密码破译的中心，现为英国国家计算博物馆所在地。——译者注}

我要补充一点历史信息。四色问题的表述最早记载于哈密顿收到的一封信里。这封信的作者是Augustus De Morgan，时间是1852年。³哈密顿当时对这道题并没什么兴趣。他在回信里写道：“我最近不太可能尝试你的‘四元色问题’⁴。”

_{3. 哈密顿写给德·摩根的这封回信上的日期是1852年10月26日，在一本非常精彩的哈密顿传记作品中有记载，参见Thomas L. Hankins: Sir William Rowan Hamilton, Johns Hopkins University Press, 1980。}

_{4. 此处哈密顿的表述为“quaternion of colours”，而quaternion表示哈密顿发明的四元数，故称“四元色问题”。——译者注}

2.2.5 数学谱系

数学家都喜欢对学术传承关系追本溯源，从自己的博士生导师，到导师当年的博士生导师，再继续这样一步一步追溯回去。数学谱系计划网站（The Mathematics Genealogy Project Web）由北达科他州立大学管理，收录了130 000多条博士生导师的记录，目标是汇集世界上所有数学家的信息。¹我很自豪，因为我自己的学术源头可以追溯到维多利亚时代的数学家Arthur Cayley，然后可以不太正式地直接跳到哈密顿爵士本人。

_{1. 该网站地址为http://genealogy.math.ndsu.nodak.edu，截至2012年12月，已收录166 000多条记录。——译者注}

我和Cayley之间的学术传承关系是直系的，回溯路径是：W. Cook（作者本人）——U.S.R. Murty——C. R. Rao——Ronald Fisher——James Jeans——Edmund Whittaker——Andrew Forsyth——Arthur Cayley。正式的追溯路径至此就结束了，因为Cayley当年学的是法律，并没有取得博士学位。但是他对数学深深着迷，并在1848年前往都柏林的圣三一学院，参加过哈密顿关于四元数的讲座。他受到哈密顿的影响，一面从事法律工作，一面继续数学研究，总共完成了几百篇数学论文，因此于1863年被任命为剑桥大学的赛德勒数学教授²。尽管Cayley并没有继承哈密顿对TSP相关问题的兴趣，但是他却是图论领域的著名人物。我们稍后会讲的“树”的概念就是由他提出的。

_{2. 赛德勒数学教授（Sadleirian chair of mathematics）是剑桥大学纯数学教授荣誉职位，因Lady Sadleir遗愿而设立并得名，Cayley是第一位获此殊荣的数学家。——译者注}