4.2 扩充构造树与路线

无论是在白纸还是在木制模型上勾画路线，思路都有一点别致之处：先选取一个出发点，然后逐步扩展出一条路线，扩展的过程可以理解为依次加入其他地点，也可以理解为依次加入其他路段。Dantzig等人凭借直觉决定每次应该选择哪枚钉子，但简单的算法也可以像样地完成任务。

4.2.1 最近邻算法

在从头开始构建路线的时候，最容易想到的方法就是每次都在没有到过的城市中选择最近的一个。这种算法称为最近邻算法（nearest-neighbor algorithm），看起来合情合理，然而得到的路线通常不是最短的。

对于42座城市的删减版题目，根据Dantzig等人提供的距离数据，可以按照最近邻算法求出一条路线。分步过程如图4-3所示。这条路线从菲尼克斯（Phoenix，凤凰城）出发，很快在美国南部延伸开来，前面若干步看起来都很不错，但是到了太平洋西北地区以后就会发现，除了一路回到东海岸以外别无选择，因此接下来只能把之前满不在乎地漏掉的城市一个一个补回来。使用最近邻算法的后果一贯如此，前进的时候目光短浅，最后总会把自己逼入死角。图4-3最后得到的完整路线长度为1013个单位长度，而Dantzig等人得到的最优路线仅为699个单位长度。

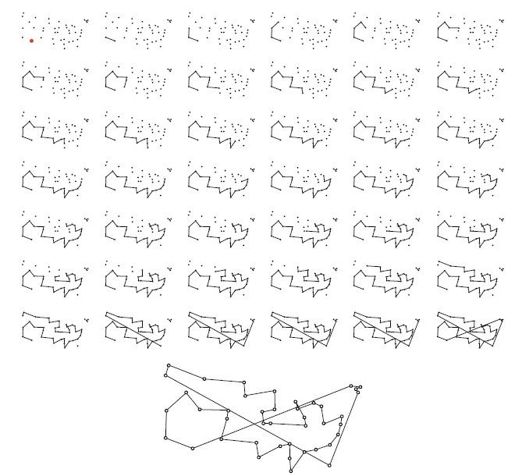
图4-3　基于最近邻算法构造路线

如果你想故意抬扛，也很容易设计一道TSP的题目，让最近邻算法得到的路线非常长，和最优路线相比简直糟糕透顶。重点就是，旅程的最后一程必须从最后一座城市回到出发地，无论这条路有多远都别无选择。所以，如果让蒙彼利埃和菲尼克斯之间的距离增加1 000 000个单位长度，很不幸，最近邻算法还是会得到同一条路线，而且这次的长度为1 001 013个单位长度，而最优路线不受影响，依然是699个单位长度。

上面这种修改方式比较无耻，得到的TSP题目虽然在数学上是合乎规定的，但其旅行距离的情形却违背了实际的道路情况。实际上，任何合理的TSP题目都应该满足三角不等式：对任意三座城市A、B、C，从A到B的路程加上从B到C的路程应该大于等于从A到C的路程。有了这条限制，上面那种没素质的题目就被排除在外了。事实上，对于n座城市的TSP题目，若其旅行成本对称且满足三角不等式，则可以证明最近邻路线成本不会高于最优路线成本的1+log(n)/2倍。因此，当城市数为50时，最近邻路线必然不超过最优路线的4倍；城市数为一百万时，最近邻路线不超过最优路线的11倍。你如果指望用最近邻算法做旅行计划，可能看到这里还是不放心。没关系，接下来介绍的其他算法可以保证更好的结果。

^{1. 本书用到的对数（log）均以2为底。}

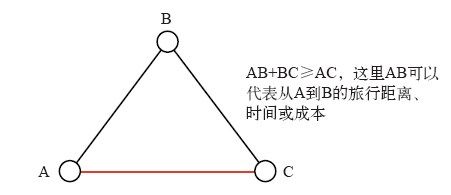
图4-4　三角不等式

4.2.2 贪心算法

最近邻算法只会生成一条路线。这条路线四处曲折延伸，最终遍历所有城市，其中每一步都选择最短的一段路程，因此这种算法非常贪心，但是“贪心”一词却被用来命名另一种算法¹。贪心算法（greedy algorithm）同时生成许多段子路线，每一步都把最短的可用路线片段加入解集中。同样以环游美国问题为例，图4-5中给出了贪心算法求解路线的分步过程。每次新增的子路线位置分散在地图各处，但最终连成了一条完整的路线。

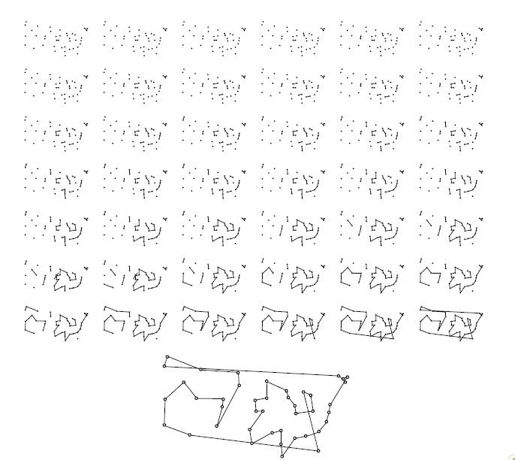
图4-5　基于贪心算法构造路线

^{1. 最近邻算法也是基于贪心算法的思想，因此有时它也称为贪心算法的最近邻点策略，而这里介绍的贪心算法则称为贪心算法的最短链接策略。——译者注}

用图论语言可以很方便地描述贪心算法这样的TSP解法，其中图的顶点就是城市，图的边则是城市之间的路线片段。最终路线是图中一条哈密顿回路，选择的边与旅行商实际出行的路段相互对应。

贪心算法以最短边优先为原则。如果一条边不能连接两条子路线，形成更长的子路线，就不会把它加入解集。按照这个算法求解路线时，起初会让人莫名其妙。在环游美国的例子中，大约前20步生成的边都确实相当短。问题出现在求解过程的最后几步，因为这时我们为了把子路线全都连接起来，不得不接受几条非常长的边，结果导致总路程长达995个单位长度。

如果测试范例很大，贪心算法几乎总是明显优于最近邻算法。试举一例，若城市在正方形内随机分布，以直线距离作为每段路程，则贪心算法得到的路线长度一般不会超过最优解的1.15倍，而最近邻路线长度则通常不超过最优解的1.25倍。遗憾的是，这个数据只是实验观察得到的。目前已知在最差情况下，对于满足三角不等式的题目，贪心算法的路线长度只能保证不高于最优解的1/2+log(n)/2倍，因此只是比最近邻算法好一点点而已。

4.2.3 插入算法

1954年，Dantzig等人借助钉绳模型获得了环游美国问题的最优路线，但是进一步的研究工作不可能指望用这种方法取得最优路线，所以当时人们面临一个紧迫的问题：他们的成功与钉绳模型的关系有多大？第二年夏天，年轻的兰德公司研究员John Robacker为此投身TSP研究，由随机路线出发，用Dantzig等人的方法，做了一系列试验，成功解决了好几道包含9座城市的题目。这些题目规模太小，说服力不强，但他还描述了通用的路线求法。如果题目的数据集很大，这种方法可以实现自动化。¹

^{1. Robacker, J. T. 1955. RAND Research Memorandum RM-1521.}

根据这些试验研究，A. W. Boldyreff提出了求近优路线的一系列步骤。他的方法具有两大优点：原理简单，使用快捷。以环游美国49座城市的题目为例，最优路线为699个单位长度，而这种近似算法求出的近优路线则为851个单位长度，误差为20%。

这种算法的思路是从一条周游几个城市的子路线出发，逐个增加新的城市，让路线像橡皮筋一样扩展，从而包围更多的城市。

由Boldyreff和Robacker提出的技巧，可以得出一类方法，统称为插入算法（insertion algorithm）。按照选取城市的具体规则，插入算法可分为几种，分别为最小插入法（cheapest）、最近插入法（nearest）、最远插入法（farthest）、随机插入法（random）。无论是哪一种插入算法，在插入新城市时，都会选择路线上最合适的位点，使插入后的路线长度最短。

最小插入法就是Robacker介绍并试验的方法，每次选择城市的原则都是使插入后的路线长度最短。最近插入法每次比较所有剩余城市到当前子路线上每一座城市的距离，选择相距最近的一对城市，其中，不在当前子路线上的城市就是要插入的。最远插入法则相反，每次选择的城市都是距离当前子路线上任意城市最远的一座。而随机插入法每次都是随机选择，把剩余城市中任意一座插入到子路线中。

在这些算法中，我最喜欢最远插入法，因为它一开始就能把握路线的整体形状，在插入城市的过程中也会不断完善细节。以环游美国问题为例，图4-6给出了最远插入法的分步求解过程。出发点是菲尼克斯，前五步就扩张到新奥尔良、明尼阿波利斯，还有两个波特兰市²，然后逐渐构造出一条778个单位长度的路线。

^{2. 美国有两座城市都叫波特兰，分别位于美国西北部（属于俄勒冈州）和东北部（属于缅因州）。——译者注}

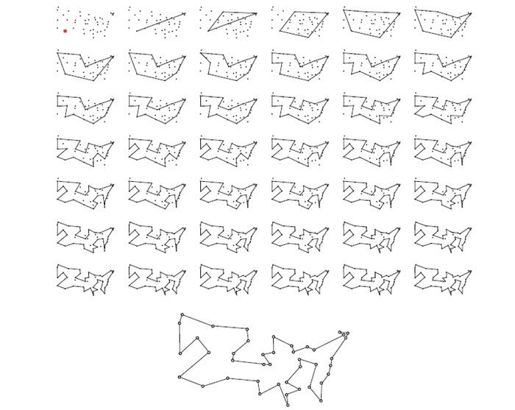
图4-6　基于最远插入法构造路线

研究表明，在满足三角不等式的条件下，最小插入法和最近插入法都相当不错，得到的路线长度不会超过最优路线长度的2倍。³虽然在实际应用中，最远插入法往往效果最好，但奇怪的是，在理论上，其路线长度只能保证不超过最优路线的log(n)倍。

^{3. Rosenkrantz, D., et al. 1977. SIAM J. Computing 6, 563–581.}

4.2.4 数学概念：树

最近邻算法和贪心算法往往虎头蛇尾，最初的选择似乎很合适，最终的路线却总是令人失望。对旅行商来说，贪心没有好结果。然而出人意料的是，对于一道与TSP相关的题目，确实有一种贪心算法能保证得到最优解。这道相关题目是给定一组城市，要求选出一系列道路，能够连接所有城市，并且总成本（代价）最小。对于环游美国问题的数据集，最小代价的道路结构如图4-7所示。道路总长度为591个单位长度，因此比最优路线还短不少。

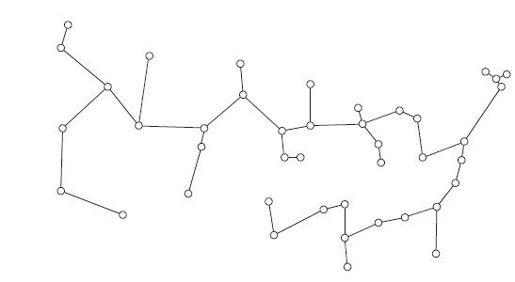
图4-7　最优树

我的曾曾曾曾曾祖师爷Arthur Cayley研究过这样的图。观察图4-7，请注意，这种结构是连通的，而且不包含回路。Cayley给此类图起了一个合适的名字：树（tree）。同时，他还把图的顶点称为“节点”（knot，该词也可表示“树的节疤”）。因此他的数学著作读来颇有植物学韵味：“在一棵有N个节点的树中，随意选择一个节点作为根节点，便可以认为这棵树是从根节点生长而成的，故称为有根树。”¹我们这里并不介绍如何从根节点生成一棵树，而是利用树的结构给出TSP的一种解法，并且同样可以保证这种解法得到的路线长度不超过最优路线的2倍。顺便一提，在电影《心灵捕手》中，马特·达蒙（Matt Damon）饰演的男主角解决了一道神秘的数学题，那道题目就是关于树的。图4-8是影片中的一幕，他写了几行字，描述了用来计数包含n个顶点的树的Cayley公式，还画出了几棵顶点较少的树。

^{1. Cayley, A. 1881. Am. J. Math 4, 266–268. 原文为“In a tree of N knots, selecting any knot at pleasure as a root, the tree may be regarded as springing from this root, and it is then called a root-tree”，其中“knot”有“节点”和“树的节疤”两层意思，“root”也有“根节点”和“树根”两层意思，故有此言。——译者注}

图4-8　马特·达蒙在电影《心灵捕手》中的形象，版权归米拉麦克斯影业公司（Miramax Films）所有

对于那个相关的道路连接问题，最优解确实就是一棵树。你大概已经凭感觉相信了这一点。关键在于，在建设道路网的时候，绝对不能形成回路，否则回路的最后一条边就是冗余的，因为它连接的两座城市之前已经通过其他道路连接起来了。这种情况下，使用贪心算法时，应该以最短边优先为原则。如果通过已经选择的其他边，可以从一条边的一个端点到达另一个端点，那么就不能把这条边加入解集。按照贪心算法，在求解过程中，各点会逐渐连接起来，形成分散的几大部分，各部分规模越来越大，最终生成一棵包含所有城市的树。不难证明一个出色的结论：根据这种简单的方法得到的树一定是最小代价生成树，也就是说总成本一定是最小的。²

^{2. Kruskal, J. 1957. Proc. Am. Math. Soc. 7, 48–50.}

树并不是环形路线，但是可以给出周游各城市的方式，下面给出一种做法。在一棵树中，到达一座新城市后，如果有一条边从这座城市出发，尚未经过搜索，便沿这条边继续前进，到达另一座新城市；否则，如果从这座城市出发的所有边都已搜索过，则逐个回溯之前访问的城市，直到发现某座城市连接的某条边未经搜索为止。重复上述过程，最终会到达所有城市，并回到出发点。这样的路线称为按照深度优先搜索算法（depth-first search）遍历（traversal）一棵树。

深度优先搜索过程如4-9所示。图中的树有6个顶点（城市），虚线表示未经搜索的边，单实线表示经过一次搜索的边，双实线表示经过搜索和回溯的边。请注意，在结束时，每条边都刚好走过两次，这就意味着旅行路线的成本是树的代价的两倍，而最优树的代价不可能超过最优路线的成本，因此这个结果很不错。要想根据遍历路线得到一条实际路线，只需跳过回溯步骤，抄条近道即可。在图4-9的最终路线中，这些近道以红线表示。

图4-9　根据树的遍历构造路线的步骤

按照这种算法，可以构造出环游美国问题的路线，长度为823个单位长度。如图4-10所示，深度优先遍历的起点是菲尼克斯。搜索过程中，如果从一座城市出发有多条未经搜索的边，总会选择对应最小子树（即子树上的城市数目最少）的一条。

图4-10　基于最优树构造路线

4.2.5 Christofides算法

为了给旅行商指路，“种”一棵树是个不错的主意。若想充分发挥树的作用，需要退一步，从莱昂哈德·欧拉的角度思考问题。把一棵树的每条边复制一遍可以生成一个图，按照深度优先搜索算法遍历树的路线实际上相当于周游对应的图的欧拉回路。复制的目的是保证图的每个顶点都连接偶数条边，不会像哥尼斯堡七桥问题那样出现奇点。¹

^{1. 无向图存在欧拉回路的充要条件是每个点都是偶点且该图是连通图。奇点（odd vertex）就是连接奇数条边的顶点。——译者注}

我们也可以不复制整棵树，而是对树添加一组边，使每个奇点连接的边数都增加一条。这样一来，生成的图中便没有奇点，因此必然存在欧拉回路，可以截短取直，得到一条周游路线。下面以环游美国问题为例说明这种思路。如图4-11所示，这道题目的树总共包含42个顶点，左图用红色标出了24个奇点，右图中共有12条边染成红色，恰好连接这些奇点各一次。²这样的一组边称为一个完美匹配（perfect matching）。Jack Edmonds提出了一种解法，可以在多项式时间内计算出最小代价完美匹配。在最优化领域，这一结论具有里程碑地位，相关内容将在第6章具体讨论。现在，我们暂时只需要知道，因为最优匹配的代价至多只有最优路线的一半（原因稍后阐明），所以最小代价完美匹配就是最合适、最完美的匹配。把树和其最优匹配相结合，在新的图中截出一条欧拉回路，便得到了一条TSP路线，其长度不超过最优路线的1.5倍。在理论上，这样的性能保证已经很不错，而实际使用时，往往可以得到更好的结果。对于环游美国问题，分步求解过程如图4-13所示，最终路线长度为759个单位长度。

^{2. 原文误作26个奇点和13条边。——译者注}

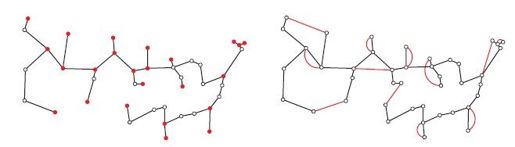
图4-11　对于奇点的最小代价完美匹配

图4-12　Nicos Christofides，1976年

图4-13　基于Christofides算法构造路线

为了从整体上估算最优路线的长度，首先要注意，在图上沿TSP路线前进时，会从一个奇点到达另一个奇点，间或穿插几个偶点。如果抄近道，只走奇点，则得到一条周游所有奇点的回路。这条回路可以分拆成两个完美匹配，从某条边开始的第1、3、5…条边组成了一个完美匹配，第2、4、6…条边也组成一个完美匹配。这两个完美匹配中，必有一条的长度不超过奇点回路长度的一半，而Edmonds的最优匹配只可能更短，不可能更长。大功告成！这三步分析如图4-14所示。环游美国的最优路线先被截短，得到一条周游奇点的回路，然后拆分形成两组完美匹配。

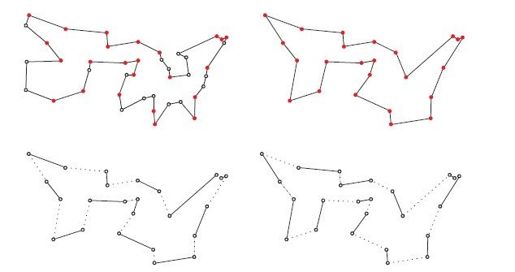
图4-14　从周游42座城市的最优路线得到两组完美匹配

1976年，Nicos Christofides首次完整提出这一算法，将欧拉和Edmonds的结论结合在一起。Christofides算法在TSP的神殿里占有重要地位，因为已知的其他多项式时间算法都无法保证给出更短的路线上限。³

^{3. Christofides, N. 1976. Report 388, GSIA, Carnegie Mellon University.}

4.2.6 新思路

从零开始逐段构造路线的过程简单而纯粹，因此常常吸引新人参与TSP研究，激发新的解题思路，也非常适合亲身体验TSP的复杂性。

如果你有意求解这道题，那么显然有一个目标：改进Christofides算法的性能保证。然而，我有必要警告你，Christofides算法保证路线长度不超过最优解的1.5倍，你可能很难突破这一结果，原因详见第9章。另一方面，如果在实际应用中，新方法能够与已有的路线构造算法一较高下，也是不足为奇的。除了已经讨论的几种著名算法以外，TSP爱好者和研究者也提出了大量其他方法，包括聚类技术、划分算法、空间填充曲线，等等。目前，在实际计算领域，上述路线构造算法的效果都不如下一节介绍的路线改进方法，但是新的思路完全有可能缩小两者之间的差距。