4.1 周游48州问题

这道难题流行于20世纪40年代，题目是给一名旅行商设计路线，让他以华盛顿特区为起点和终点，周游美国本土的48个州。Julia Robinson建议把各州首府指定为旅行商的目的地，从而限制了路线的范围。尽管只需把各段路程的数值列成表格，就可以彻底明确题目叙述，但是当初似乎没有人做这一步工作。很可能是因为，在当时的人们看来，如此大规模的TSP题目超出了他们的解决能力。

显然，Dantzig、Fulkerson和Johnson并不这么认为。由于无法获得城市间路程的标准数据集，他们自己动手给出了一组数据。由图4-1可见，他们选择的城市与前人的限定大不相同，在分别选自各个州的48座城市中，只有20座是所在州的首府。这种背离传统的选择却并非出于什么神秘的原因。“我们之所以选择这组城市，是因为很容易在地图集里查出其中大部分道路的里程。”¹有道理。这一选择尽管理由简单，但在TSP计算中，确实直接带来了好的开始。因为在他们使用的兰德麦克纳利标准地图集中，从华盛顿到波士顿的最短路线会经过美国东北部的另外7座城市，这些城市也在旅行商的目的地之列。于是，他们决定不考虑这7座城市。这样做有点冒险，论证过程如下：在周游剩下42座城市的最优路线里，如果有一段是从华盛顿直接开车前往波士顿，那么他们只需要在路过巴尔的摩、威尔明顿、费城、纽瓦克、纽约、哈特福德和普罗维登斯的时候，摇下车窗挥手示意就可以解决原题了；但是另一方面，周游其他城市的最优路线也可能以另外的方式到达华盛顿，若真如此，就只能换种思路从头再来了。

_{1. Dantzig et al. (1954).}

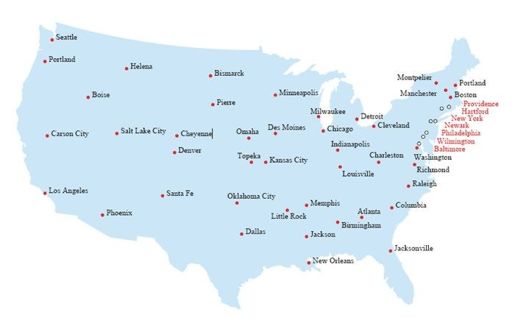
图4-1　周游48州问题里的各大城市

看看地图，很容易猜到，最优路线大概会用到直接连接华盛顿和波士顿的这条路。实际确实如此。因此，兰德公司的Dantzig等人确实有理由只考虑剩下的目的地。然而有必要指出，放在今天就没有这么顺利了。通过谷歌地图（Google Maps）可以测得，从华盛顿到波士顿的最短路程是451英里（756千米），但是假如要求经过那7座城市，这段路就变成491英里（790千米）了。同样是从康涅狄格州一路开入马萨诸塞州，前者之所以能节省路程，主要是因为用到了84号州际高速公路。但是这段高速公路直到1967年才通车。

Dantzig等人当时由兰德麦克纳利地图查得的数据是对称的，城市两两之间的距离与行车方向无关。（在本章中，我们假定旅行成本是对称的。²）他们处理了初始数据，把每段距离值先减去10，再除以17，然后四舍五入，取最接近的整数。“我们选择这样的变形，是为了把原始表格里的d_ij数据都变成小于256的整数，以压缩用二进制形式存储距离表所需的空间，实际并没有什么用。”³他们的论文列出了处理后的距离数据表，从而明确提供了这道题目的条件。

_{2. 本书重点始终是对称形式的TSP，也就是旅行成本（路线长度）与旅行方向无关的情形，即从城市A去城市B的旅行成本与从城市B返回城市A相同。这一限制主要是为了控制讨论的篇幅，但是请不要认为作者有意蒙混过关，因为可以证明：任意包含n座城市的TSP题目都可以转化为2n座城市的对称TSP题目。}

_{3. Dantzig et al. (1954).}

钉子和绳子

Dantzig等人的数据并没有使用两点之间的真实距离，因此稍微改变了问题原有的几何学本质。不过，如果数据取为两点之间的直线距离，也就是欧几里得距离（欧氏距离），可以有效提高比较路线长度的效率。事实上，他们当时的解法就完全建立在这种近似的基础之上。

他们在原始论文里给出了一条周游美国的路线，对得到这条路线的方法却只字未提。随后，Dantzig在讲座中透露，研究小组当时使用了一个实物模型。模型是木质的，由他们自制而成，上面标有题中的49个地点，每处都有一枚钉子。代表出发地的钉子上系了一根细绳。他们把这根绳子依次绕过其他钉子，便勾画出一条路线。

图4-2　根据钉绳法构造周游德国的路线（德国柏林祖斯研究院供图）

Dantzig表示，这个模型是他们手工解题的得力助手。绷紧绳子测量绳长就可以获知路线的长度，也能很快直观看出下一段子路线的可能走向。这个模型完全没有提供解题的算法，却帮助Dantzig等人确定了一条周游所有城市的路线。并且他们后来证明，这条路线就是所求的最优路线。按照处理后的数据表来计算，周游美国的最优路线长度为699个单位长度，换算成地图集上的实际距离则是12 345英里（即19 867千米）。