5.5 消去子回路

在TSP的线性规划解法中，下一步是引入一系列简单而强有力的附加规则。为此，我们再次考虑图5-5中包含6座城市的控制区分布示意图。该图中，控制区连成环状分布，很容易勾勒出一条路线，穿过各个控制区，完全不浪费任何空间。然而，一般情况下我们并没有这么幸运。如图5-7所示的现象更为常见，图中各个控制区挤成好几堆，因此勾连路线时不得不留出一大截空隙。新规则利用的正是这样的空隙。

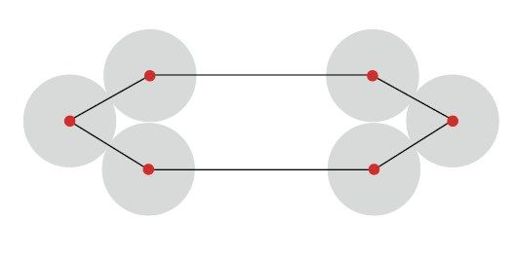
图5-7　不合适的控制区分布

下面我们描述一下新规则的几何思想。在控制区分布剩下的空隙中，可以围绕一堆点的团簇，画一条环带，如图5-8所示。任何一条路线必然在某一刻到达这一簇点，旅行商进出这组城市时，每一程都必须经过这个环带，所以总共至少要经过两次。因此，控制区给出的路线长度下界中可以加上环带最小宽度的两倍。Jünger和Pulleyblank把这样的环带称为“护城河”（moat），因为它们确实就像护城河一样。

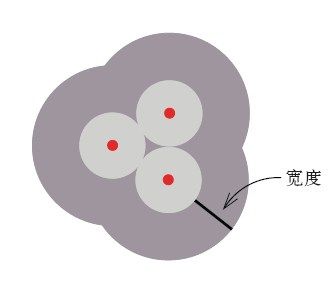
图5-8　护城河区域

如图5-9所示，在6座城市的题目中，可以使用两个护城河区域弥合控制区之间的空隙，这样一来，沿着城市勾画路线时，便同样不会浪费任何空间距离了。虽然我们并非次次都能如此幸运，充分利用一切边角空间，但是只要仔细安排护城河和控制区的分布，通常依然能够给出很强的路线长度下界。以图5-10为例，这里有100座城市，图中的分布很合理，足以证明给出的路线长度最多只比最优路线长0.65%。

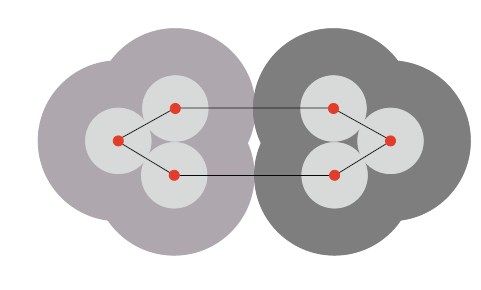
图5-9　用护城河弥合控制区之间的空隙

图5-10　护城河和控制区的综合分布

这个100座城市的例子很漂亮，不过如果想要更好地理解这种路线的下界，最好选择规模更小的题目实际演练。在此，我向读者推荐Geodual软件包，它是由德国科隆大学的Mike Jünger研究团队开发的。¹该软件能够为20座城市左右规模的TSP题目给出最优解，同时还会提供一幅优美的护城河和控制区分布图，成果一例见图5-11。

图5-11　Geodual求解15座城市的TSP时的真实截图

^{1. 参见http://www.informatik.uni-koeln.de/ls_juenger/research/geodual/。}

5.5.1 子回路不等式

在一些TSP题目中，我们如果想用原始解构造一条路线，就会遭到度约束线性规划的松弛的无情捉弄。图5-7的6座城市TSP便是如此。事实上，考虑到跨过巨大空隙的边会有高昂的旅行成本，单纯形算法给出的解会包含两个三角形，而不是一次性走过全部点的完整回路。显然，这虽然是松弛问题的可行解，对旅行商而言却并不可行。

注意到有些边跨越城市团簇之间的空隙，如图5-12的绿色线段所示，而所有路线都必定包含至少两条这样的边，于是我们能直接做出简便的补救。仿照Jünger和Pulleyblank构建护城河的思路，我们可以提出一条规则：对应这些跨团簇的边的变量之和至少为2。

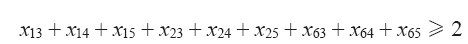
图5-12　构成子回路不等式的边

有了这个不等式，再加上度约束条件，图5-12的解便不可能包含左图中红边组成的子回路了。因此，这条规则称为子回路消去约束条件（subtour-elimination constraint），简称子回路不等式（subtour inequality）。

对于全部城市的任意适当子集S，因为一端在S中而另一端不在S中的边所对应的变量之和至少为2，可得到一个子回路不等式。图5-12中有S={1, 2, 6}，而图5-13展示的例子规模更大，落在矩形框内的顶点构成了集合S，而染成绿色的各边对应于相应的子回路不等式中的各个变量。

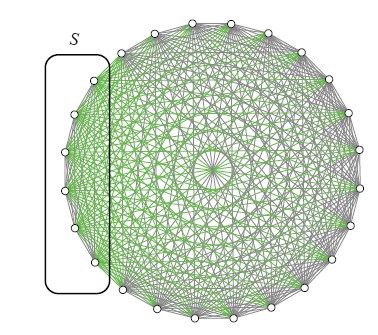
图5-13　构成子回路不等式的绿边

这些附加规则虽然简单，但通过线性规划结合在一起时却能带来巨大的威力。度约束线性规划的松弛和所有的子回路不等式联合起来，构成的模型称为子回路线性规划的松弛（subtour LP relaxation）。事实上，这种方法可以获得优质的路线长度下界，其结果对实际应用线性规划成功求解TSP举足轻重，功不可没。对于随机生成的几何题目，子回路方法给出的下界几乎每次都与最优路线相差不到1%。如果选取42座城市的环游美国数据集为例，可以看到，得到的路线长度下界是697个单位长度，而最优路线为699个单位长度。在这一特例中，与理论的品质保证相比，实际的最优路线仅仅超出0.3%而已。

5.5.2 “4/3猜想”

总体上，我们并没有这么强的品质保证，幸好，糟糕的反例看来只是偶然例外，优良的范例才是正常规则。对于满足三角不等式的题目来说，如何才能判断路线长度下界质量是好是坏？这是一个颇有意味的问题。从乐观的一方面来看，人们已经知道，最优路线的成本必然不会超过子路线下界的3/2倍。比起前一章介绍的Christofides定理，这个理论结果很出色。

但是凡事都有两方面，这个问题的负面则在于，人们已经发现了一系列题目，当城市数目增大时，它们的最优路线成本与子路线下界之比将逐步逼近4/3。4/3这个数字就是最差的可能性吗？这个问题称为“4/3猜想”（4/3rds Conjecture），加拿大渥太华大学的Sylvia Boyd是钻研该问题的顶尖专家。她与同事通力合作，已经验证确定，在不超过十座城市的所有情形下，该猜想都成立。她还提出了一个更尖锐的问题，有可能为完整解决猜想、证实最终结论提供必要的思考方向。¹

^{1. Benoit, G., S. Boyd. 2008. Math. Oper. Res. 33, 921–931.}

品质保证从3/2升级到4/3，看似只是一小步改进，但基本上，要想迈出这一小步，必须深刻理解子回路线性规划的松弛问题的可行解结构。²反过来，这样的理解也会产生新的TSP方法，提出新的解题规则，从而有机会推动实际计算超越现有的极限。

^{2. 麻省理工学院的Michel Goemans已经证明了若干与子回路LP松弛之解有关的重要结论。}

图5-14　Sylvia Royd和Richard Haynes（左），Bellairs Workshop 2007，Nick Harvey摄；“4/3猜想”文化衫图案（右），由Bill Pulleyblank设计

5.5.3 变量取值的上界

此前没有解释过，度约束线性规划的松弛之所以非比寻常，是因为该题目必然存在所有变量取值均为0、1或2的最优解，所以我们完全不必担心边取分数值的问题。子回路的松弛并没有这个结论，它的变量赋值有时候也会出现复杂麻烦的分数。最终，我们有必要从整体上处理一般情形，但是有价值的特例能让我们赢在起跑线上。事实上，在度约束线性规划的解中，如果变量x_ij取值为2，就意味着对应的子回路只包含城市i和城市j一来一回的两段路途。根据S={i, j}确定的子回路不等式，可以排除这种情形，但是简单规定x_ij≤1可以更方便地解决这个问题。这样一来，不但使用度约束，而且限制所有变量的取值上界，就比只用度约束的基础效果更好，所以实际应用往往都采取这种做法。另外，在改进之后，初始模型必然存在所有变量取值均为0、1/2或1的最优解。它虽然不完全是整数解，总算也是八九不离十了。