5.6 完美松弛

借助子回路不等式，我们可以将TSP的解限制在最优解附近，那么，能否再添加其他规则，大大改进所得结果呢？没问题，放心吧，能！要进一步改进结果，需要用到少许数学知识，马上你就明白了。

5.6.1 线性规划的几何本质

迄今为止，我们处理线性规划时，一直在对变量和方程进行运算，把它视为单纯的代数问题。对George Dantzig和大多数线性规划研究人员来说，这样的待遇是不公平的。在他们心目中，线性规划独具一种优雅的几何韵味。

下面，从一道小例题出发，我们试着回顾一下之前忽视了什么。

目标：x+2y取最大值

约束条件：

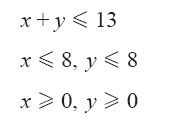
我们可以把该题的可行解理解成二维平面内的点(x, y)，这里x和y的数值分别由水平方向和垂直方向的数轴确定。

在一道线性规划题目中，全部可行解的点构成的集合称为可行域（feasible region）。为了理解可行域的范围，首先只看第一个约束条件x+y≤13。相应的直线x+y=13把所有形如(x, y)的点划分成两个集合，分别位于直线两侧，直线一侧的点都不是可行解，而直线另一侧的点以及直线上的点都是这个约束条件的可行解。可行解所在的一侧区域称为半空间（halfspace）。图5-15给出了半空间的两种不同表示形式，左图中红色箭头指向可行域一侧，右图中可行域则涂成了红色阴影。

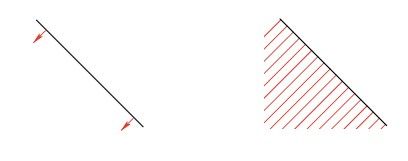
图5-15　由一个线性不等式确定的半空间

上面的线性规划例题中，有五个线性约束条件，对应五个半空间，它们的交集就是题目的可行域，如图5-16所示。在这个几何模型里，右侧小图中的蓝色直线代表目标函数，线性规划问题的目标就是尽力向上移动蓝线，同时保证它与可行域有公共点。因此，本例题的最优解就是图中的红点，坐标为(5, 8)。

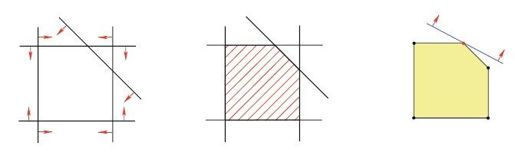
图5-16　从几何角度理解线性规划问题

请注意，最优解是可行域的五个顶点之一，另外四个点按顺时针顺序依次为(8, 5)、(8, 0)、(0, 0)和(0, 8)。在这道线性规划题目中，有一个重要结论：无论目标函数如何设定，这五个顶点中必有一个是最优解。事实上，改变目标函数就意味着改变蓝线的斜率，而尽力向某个方向移动直线时，无论移动方向如何，直线在即将离开可行域的瞬间都必定刚好触及可行域的一个顶点。

上述一般性质非常有用，它意味着线性规划问题虽然有无穷组可行解，但求解时只需要考虑顶点即可，而顶点的数目是有限的。事实上，单纯形算法的过程可以理解为沿着可行域边界移动，顺次经过各个顶点。

读到这里，你可能会问：既然只需要把顶点列出来就能解决线性规划问题，为什么还要大费周章地使用单纯形算法呢？原因归根结底在于数字。请记住George Dantzig的话：“对于大规模的问题，组合（顶点）的数目有可能非常多，可能像天上的星星一样多。”在d维空间里，一系列d维半空间的边界面相交，就得到线性规划模型的顶点。这样的交点未必总会落在可行域里，但是已经足够让试图列出所有顶点的解题者为之头疼了。

5.6.2 闵可夫斯基定理

刚才我们讨论的对象是线性规划问题的顶点，但是具体说到TSP，情况就完全相反了。对于TSP，我们已经有了所有点的完整列表，它们分别对应于图里的各条回路，但是我们却并不知道线性规划模型的可行域是什么样的。从这种角度看来，搜寻TSP规则就等于搜寻能够限制回路范围的半空间。

让我们研究得更仔细一些。在6座城市的TSP里，每条完整路线都对应于15维空间里的一个点，这15维空间里的每个维度都对应于一对城市。每个路线点的坐标都由0和1组成，其中1表示路线用到了相应两座城市之间的边。这些坐标取值或为0或为1的点组成了一个很大的集合，虽然它们都落在15维空间里，但是当我们想选出对应最短路线的点时，却没有任何可供使用的几何结构。线性规划的作用正是弥补这一缺陷。

15维空间的图像是画不出来的，所以我们转而思考二维空间的类似问题，也就是从一组形如(x, y)的点里选出一个，使某个确定的目标函数在该点处取得最大值。这里，我们要找这组点都满足的线性不等式，换言之，使这组点都落在可行一侧的半空间。如图5-17所示，根据实际题目可以逐步构造合适的不等式，最终在给定点集周围得到6个半空间，这些空间的中心区域的每个顶点都是题目条件给定的点。根据线性规划，这个结果具有出色的推论：对所得区域应用单纯形算法，便可以得到原题的最优解。

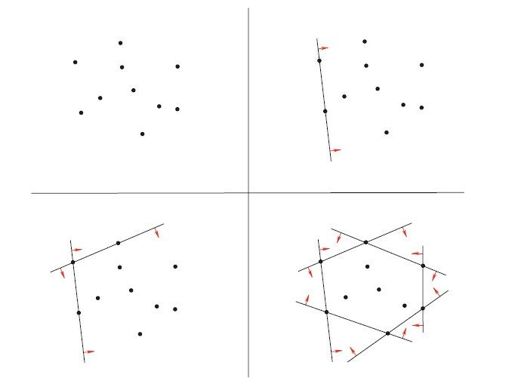
图5-17　构造线性约束条件

图5-18再次展示了图5-17最终得到的区域。该区域之所以构造得天衣无缝，并不仅仅出于偶然运气而已。实际上，我们可以通过合理构造，让任意点集都落在线性规划的可行域内，使得可行域的每个顶点都是点集里的一个点。如果是在二维空间里，请想象把一根橡皮筋抻开，然后松手让它收紧，套住所有的点；在三维空间里，请想象用塑料薄膜裹住所有点，然后加热使薄膜缩紧，再次形成完美贴合。如果维度继续增加，那么很难进行形象化的想象，但是结合代数学和几何学，不难证明相应的结论。这个结论最初发现于20世纪伊始，发现者是（赫尔曼·闵可夫斯基）Hermann Minkowski。

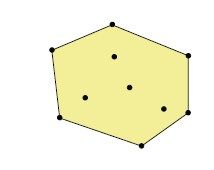
图5-18　凸包

给定一个点集，恰好紧紧包围所有点的区域称为点集的凸包（convex hull）。在二维空间里，凸包是一类特殊的多边形。在三维空间里，凸包则是具有多个小面的立体结构，像是柏拉图立体¹或者钻石经过切割以后的形状，这些形体统称为凸多面体（convex polytope），数学家从很久以前开始就一直在研究它们。Günter Ziegler在专著Lectures on Polytopes（《多面体课程》）中对这一研究领域做出了出色而严谨的介绍，这本书虽然有高深的理论细节，但是引言部分以及前几章内容都值得一读，能让你充分体会为何数学家始终对这些经典几何结构一往情深。²

^{1. 即正多面体，共五种，分别为正四面体、立方体、正八面体、正十二面体和正二十面体。——译者注}

^{2. Ziegler, G. 1995. Lectures on Polytopes. Springer, Berlin, Germany.}

5.6.3 TSP多面体

任何TSP都可以准确描述为线性规划问题，这个结论非常重要，而闵可夫斯基定理的意义完全不在前者之下！它为寻找TSP规则的行动提供了坚实的理论支持：必需的线性不等式就在那里，只等着我们发现呢。

先别摩拳擦掌，我得提醒你，求解的时候可能会遇到困难，因为描述TSP多面体所需的半空间总数相当庞大。人们已经知道，城市数目达到10座时，所需的不等式数目就至少达到51 043 900 866个。¹不过，只是数字很大的话，并不足为惧。2008年，Harold Kuhn做了一场George Dantzig纪念讲座（George Dantzig Memorial Lecture），他在演讲里强调了这一点，并在文中援引了自己在1953年的TSP研究做例子。

^{1. Christof, T., G. Reinelt. 2001. Int. J. Comput. Geom. Appl. 11, 423–437.}

整个夏天，我跟George经常联系，一直在讨论这道题目和其他题目。我知道，夏天快结束时，他来听过我的课（Selmer Johnson、Ray Fulkerson和Alan Hoffman也来了）。我们俩都很清楚，虽然在用线性规划模型描述旅行商问题的时候，面（face，约束条件）的总数是巨大的，但是只要你能找到一道松弛问题的最优解，这道题由面的子集构成，而且这个解是一条回路，那么你就解决了这一切背后的旅行商问题。

我们需要好好学习如何使用不等式，也就是如何提出对于求解的TSP题目有用处的不等式。这是线性规划求解TSP的核心所在，第6章将对此进行深入讨论。