5.2 单纯形算法
在《纽约时报》的封面上,要等多久才能看到一回数学的身影?费马大定理的证明成功登上了封面,而四色定理却不够格。至于研究线性规划的人,他们会自豪地说起两期封面故事。
一位名不见经传的苏联数学家做出了意外的发现,震惊了数学和计算机分析的世界。现在专家学者已经开始探索这一发现的实际应用。
——Malcolm W. Browne,《纽约时报》,1979年11月7日
方程系统常常变得数目繁杂,极为复杂,最强大的计算机也无法解决。如今,贝尔实验室有一名28岁的数学家在这方面实现了惊人的理论突破。
——James Gleick,《纽约时报》,1984年11月19日
上述两段评论来自两篇封面文章,分别介绍了求解线性规划问题的一种新算法,而且都是多项式时间算法。前一种算法由前苏联数学家Leonid Khachiyan发明,后一种则由贝尔实验室的Narendra Karmakar设计。
在这两篇文章中都咄咄透露出一点,Dantzig的单纯形算法在求解大规模问题时不甚实用,因此即将让出线性规划算法的王座。然而它并不会这么轻易就被推翻。20世纪80年代晚期,人们实现了新的单纯形算法程序,比如莱斯大学的Bob Bixby开发了CPLEX程序,IBM公司的John Forrest开发了OSL程序,这些都证明了单纯形算法仍有相当大的力量深藏不露。事实上,2000年评出的“世纪十大算法”(The Top Ten Algorithms of the Century)中,它的名字赫然在列,而且它至今仍在数学最优化领域不断立下汗马功劳。1
1. Dongara, J., F. Sullivan. 2000. Comp. Sci. Eng. 2, 22–23.
5.2.1 主元法求解
一代应用数学家与工程师领会了单纯性算法的实质,他们写了许多优秀的文献,用五花八门的方式描述算法的详细步骤。Vašek Chvátal的著作《线性规划》(Linear Programming)1渊博美妙,其他作品无出其右者。所以,下面我们就借助产品制造的例子,一起理解他介绍的计算步骤。
1. Chvátal, V. 1983. Linear Programming. W. H. Freeman and Company, New York.
向线性规划模型中引入产品以后,变量A、B、C就表示商品A、B、C的生产活动强度。这些数值足以彻底明确问题,但如果要向管理部门提交报告,我们可能希望在报告里附加其他信息,包括总利润Z、镍的剩余库存量N和钢的剩余库存量S。这三个新变量定义如下:
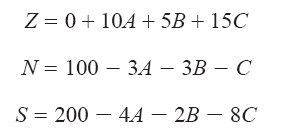
上述各式相当于用来查找这些变量数值的字典。
由这个字典可以自然想到一种赋值方式,即令A、B、C均为0,则由字典读出利润Z=0,镍存量N=100,钢存量S=200。这结果真令人失望,不过也很容易提升。以A为例,因为在利润的定义式里出现了10A这一项,而目前A取值为零,所以只要提高A的取值,那么公司就会有更多钱入账。不过在模型的约束条件下,A的产量最多可以提高到多少呢?保持B=0和C=0不变,就能满足最后三条取值非负的约束条件,不过我们还需要保证原材料镍和钢的库存够用,也就是N≥0且S≥0。N≥0意味着100/3A≥0,换言之,A最多可以取值 ,再多就没有镍可用了。同理,S≥0意味着A最多可以取值50,然后钢也就耗尽了。在这个例子中,镍就是最严格的约束因素,也就是紧约束,于是我们决定,令
,再多就没有镍可用了。同理,S≥0意味着A最多可以取值50,然后钢也就耗尽了。在这个例子中,镍就是最严格的约束因素,也就是紧约束,于是我们决定,令
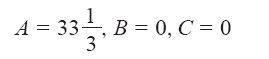
总利润为 美元。2
美元。2
2. 在线性规划模型里,必须假定允许生产、销售非整数的产品量。本章结尾将继续讨论这点。
下面,让我们看看现在取值都是零的B和C。要如何增加它们的产量呢?这次结果并不是一目了然的,因为A已经用尽了所有的镍存量,所以在增加B和C的同时,必须减少A才能有镍可用。为了明确A对B、C的影响,可以把A移到字典定义式的左端,改写上述等式。同时,由于N目前取值为零,我们要把它也移到右端。
字典中对N的定义式为
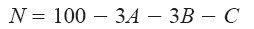
把A移到左端,N移到右端,等式两端同时除以3,就得到等价的表示式
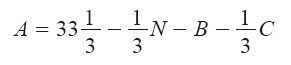
我们会在新的字典中使用A的上述新定义式,并且将它代入总利润Z和镍存量S的定义式中,从而得到方程组
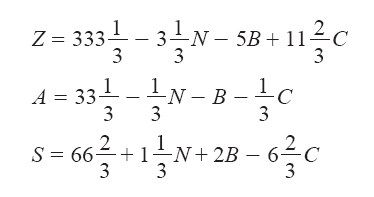
这步操作互换了A和N的地位,称为选主元(pivoting),其中A称为换入变量(incoming variable),N则称为换出变量(leaving variable)。请注意,虽然变量Z和S的定义式不同于之前字典中的形式,但是Z和S的意义依然不变,分别代表总利润和镍存量。事实上,在改写变量定义式时,由于使用的等式对任何赋值都成立,因此变量的意义都不会改变。
得到新字典之后,很自然的答案是令N、B、C均为零,读出其他各变量的值为
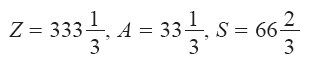
 美元的总利润肯定比零利润多,但是我们完全可以赚更多。仔细观察改写后的利润定义式,可以发现,N和B这两项的系数都是负的,因此,如果增加其中任何一个的量,就会导致总利润下降。幸好C项的系数是正的,所以下一步换主元操作时,我们就应该考虑增加C的值。
美元的总利润肯定比零利润多,但是我们完全可以赚更多。仔细观察改写后的利润定义式,可以发现,N和B这两项的系数都是负的,因此,如果增加其中任何一个的量,就会导致总利润下降。幸好C项的系数是正的,所以下一步换主元操作时,我们就应该考虑增加C的值。
下面,让我们把C作为换入变量,逐步进行换主元操作。首先,保持N和B为零,根据新字典,有

由此可知,C最多可以增加到100。类似可得
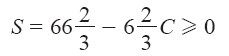
由此可知,C最多可以增加到10。又因为10<100,所以S是这一步换主元操作的换出变量。
下一步是改写字典,用S表示C并依次代入各式,具体算术过程在此略去。最终,新的方程组为
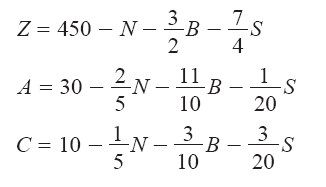
对于刚得到的新字典,自然的答案是令
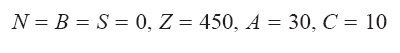
这种赋值方式就是我们在前一节宣称的最优解。你不必盲目相信我的断言,因为我们可以给出充分的证据:利润式Z=450−N−32B−74S证明了,生产商绝对不可能获得高于450美元的利润。事实上,无论如何赋值,N、B和S都必然是非负数,因此总利润就是450美元减去一个非负数。以上,证明完毕。
可以看出,单纯形算法就是这样,通过换主元操作把一部字典变成另一部字典,每一步变换都希望增加目标函数的值。如果到了某一部字典,目标函数定义式可以证明,自然解就是最优解,那么算法就终止。易如反掌,不过刚才我们有意无视了几处难点。一般来说,如何找到初始字典?如何确定算法必定终止?这些问题都可以获得解答,Chvátal对此做了详尽的分析,感兴趣的读者请参阅他的书。
如果你有意求解其他的题目,但又讨厌人工完成这么多运算,有一个网页提供了Bob Vanderbei的单纯形换主元工具(Simplex Pivot Tool)3,请上网一探究竟。这个小工具允许你以字典的形式建立起自己的线性规划模型,让你选择换入和换出变量,实现换主元操作。假如你犯了错误,选择的换出变量与紧约束条件不对应,该网页甚至会提醒你这一点。
3. http://campuscgi.princeton.edu/~rvdb/JAVA/pivot/simple.html。这是下书的相关工具:Vanderbei, R. J. 2001. Linear Programming: Foundations and Extensions. Kluwer, Boston, MA.
5.2.2 多项式时间的选主元规则
Dantzig给出了一个算法,但我们凭什么相信它是可行的,无论多大规模的题目都能解决?问得好。
2009年,计算机科学基础年会(IEEE FOCS)迎来50周年,并在亚特兰大举行了庆祝会议。Richard Karp以“优秀的算法好在何处?”为题,做了开场报告。他举了一堆优秀算法的例子,单纯形算法排在第一个,上榜理由是实际高效可行,加之应用广泛。不过Karp当时也不得不指出,在复杂度方面,单纯形算法并不优秀。事实上,它并不能保证在多项式时间内完成运行。
问题在于,虽然可能的字典数是有限的,但是这个有限的数字却是指数级的。目前人们并不知道,能否按照某种方式选择每步的换入变量和换出变量,使得只需经过多项式次数的换主元操作,就能得到最优字典。实际上,人们已经知道,有好几种思路自然的换主元规则并不是多项式的,也就是说已经针对它们构造出了特定的极端反例,导致单纯元算法按照相应的换主元规则运行时,换主元的步骤达到了惊人的指数级。
既然如此,Dantzig本人对单纯形算法的巨大信心从何而来?答案是,他其实并没有信心,至少一开始没有。1
1. Albers and Reid (1986).
刚开始,我觉得这个方法有可能效率不错,但不一定实际可行。如果题目很大,就可能有很多种组合(顶点,corner point,也称为角点或极点),说不定跟天上的星星一样多,那算法可能就需要上百万步才能解出来。这个步骤数确实比可能组合的总数要小,所以可以认为算法是高效的,但基本还算不上可行。因此,我当时就继续去寻找更好的其他算法了。
直到国防部的同事们成功解决了一道又一道难题之后,Dantzig才终于认可了自己的算法。
时至今日,情况依然如此。单纯形算法是如今数学中应用最广的工具之一,但是我们并不清楚,今后从实际模型中涌现出的问题是否一直能够迎刃而解。如果有人能回答这个问题,绝对能成为《纽约时报》的封面故事主角。如果有人能提出新的选主元规则,保证在多项式次数的步骤之内获得最优解,那么声望乃至财富都将从天而降,滚滚而来。
5.2.3 百万倍大提速
Dantzig在计量经济学会1948年年会上发表了报告,摘要只有寥寥几行,最后一句总结道:“对于由约翰·冯·诺依曼或笔者等人提出的此类计算方法,在实现规划问题的解法时,建议配合使用大规模数字计算机。”1当时,数字计算机时代刚刚拉开序幕,应用数学家已为此激动万分,Dantzig亦把单纯形算法推到了最前线,等待可能的计算机实现。
1. Dantzig, G. B. 1949. Econometrica 17, 74–75.
然而,单纯形算法的第一次大规模测试却没有用到计算机。1947年,这场计算测试在美国国家标准局举行,一群测试人员手动操作台式计算器,总计连续工作120个工日。2测试实例的原始问题是选择成本最低的日常健康饮食计划,模型包括9个约束条件和77个非负变量。在如今的工业线性规划模型中,约束条件和变量都数以十万计。当年的测试实例虽然规模挺大,相比之下也只是小巫见大巫而已。幸运的是,从当年的计算饮食计划问题到发布新型线性规划软件之间的这些年里,人们殚精竭虑,致力于调整改进单纯形算法,为程序实现做准备。
2. Dantzig, G. B. 1982. Oper. Res. Let. 1, 43–48. 工日是工作时间的计算单位,一个人工作一天记为一个工日。——译者注
在单纯形算法的发展史上,有一个阶段格外重要。1984年,Karmarkar公布了内点法(interior-point method),这是一种具有竞争力的线性规划新算法。围绕内点法的新闻报道使线性规划成为了舆论关注的焦点,性能强劲的台式工作站和个人电脑恰恰也在此时走入寻常百姓家。强强联手,线性规划世界自此跨进超光速发展时代。事实上,在1987到2002年间,基于单纯形算法的求解程序速度加快了百万倍。Bob Bixby具体解释道:“机器运行速度提高了三个量级,算法运行速度又提高了三个量级,合起来就让解题能力提高了六个量级。10年前需要花一整年才能解决的题目,如今不到30秒就能解决。”3这下,线性规划解题性能获得了可观的提升。后来的岁月风平浪静,波澜不惊,但是我们完全有理由相信和期待,研究活动继续开展下去,必将掀起新一轮突飞猛进的浪潮。许多科研项目得到了广泛的资助,尤其是来自美国国家科学基金会和海军研究办公室的大力支持。这些课题致力于促成单纯形求解程序的更新换代,新一代程序将利用未来计算机芯片的众核性能。如果历史可以为鉴,那么线性规划研究者将面对更好的硬件,并在此基础上设计出更好的实现,让Dantzig的单纯形算法不但能更快地作出解答,而且能解决更大规模的题目。
3. Bixby, R. E. 2002. Operations Research 50, 3–15.
5.2.4 名字背后的故事
单纯形算法的英文是simplex algorithm,感觉像是用simple(简单、单纯)这个词新造出来的生词一样,很有近年流行的文字游戏的味道。实际上,用谷歌搜索这个英文单词,返回的前几条结果确实如此。但是它其实是个几何学概念,表示一种经典的几何形体:单纯形,即有n+1个顶点的n维多面体(可剖分空间)。二维单纯形就是三角形,而三维单纯形则是四面体。当时,Dantzig的好友Theodore Motzkin建议,借用这个几何概念为算法命名。“‘单纯形方法’这种说法来自我和T. Motzkin的一场讨论。他觉得如果考虑列向量的几何意义,那么可以恰当地把我的方法描述为相邻的单纯形之间的变换。”1他采纳了这个建议,这实在是太遗憾了,因为“Dantzig算法”明明是个不错的名字,可以恰如其分地纪念他的杰出贡献。
1. Dantzig (1991).
