5.3 买一赠一：线性规划的对偶性

最优字典能够给出证据，证明单纯形算法已经给出了最优解，但是要说服经理相信这一点，恐怕没那么轻巧。实际上，大概没人打算把整个换主元操作序列都交给经理过目，让他一步一步验算；同样，也没法要求检验Bob Bixby的线性规划解题工具，看看它那上百万行的代码有没有问题，以确认它正确地实现了Dantzig的算法。我们需要的其实是得出字典证据的捷径，而在线性规划中，对偶性（duality）的作用正在于此。

让我们回到带有三种产品线性规划的模型里，观察最终的利润式

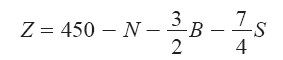
这个表达式是由Z的初始定义与所有允许赋值都满足的若干等式相加而得的。我们知道这句话是事实，可惜经理并不知道。没关系，别担心。如果我们在总利润Z的最终定义式里，把N和S在初始字典中的定义式分别代入，那么就重新得到了总利润Z的初始表达式。这样一来，经理应该可以相信，我们没有做什么手脚。不过我们可以更简洁地完成这一过程，直接证明盈利不可能超过450美元。

为了建立证明，我们首先取镍存量N和钢存量S的初始约束条件，再分别乘以总利润Z的最终定义式中相应项的系数（不带负号），得到

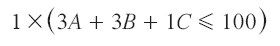
及

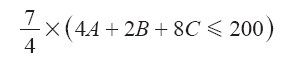
然后计算得两个新的不等式，相加得到一个不等式

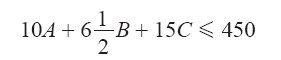
经理看到这个，肯定也会点头，同意任何可能的产品生产水平都满足上式。而与总利润10A+5B+15C相比，可以看出，盈利不可能超过450美元，就算把产品B的利润率（profit margin）提高到每单位6.5美元也无济于事。稍做几步乘法和加法，即可得出结论：我们提出的生产方案是最优的。

下面，我们回顾一下刚才证明中的几处要点。首先，我们取了N项系数和S项系数，称为y_N和y_S，它们都是非负数，因此可以用来与镍和钢的约束条件相乘。其次，相乘之后得到了两个新的约束条件，两式相加时，A、B、C前面的系数都不小于相应产品的单位利润值。

这两条规则确保我们对y_N和y_S的使用有理可依，而它们事实上正是另一道线性规划问题的约束条件。

目标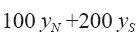：取最大值

约束条件：

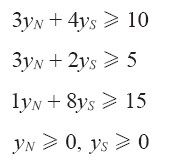
上面三个约束条件分别对应于变量A、B、C，它们可以保证，在原始不等式乘以y_N和y_S之后，得到的新不等式中，各项产品前的系数都至少不低于三种产品的单位利润值。如果y_N和y_S的赋值满足以上各条约束条件，就可以说明总利润值不会超过100 y_N + 200 y_S。因此，为了获得有说服力的证据以供给经理看，我们希望想办法使这个量取得最小值。

这个新的线性模型称为对偶问题（dual problem），按照Dantzig的父亲Tobias的建议，原始问题则称为原问题（primal problem）。对偶线性规划问题中，约束条件要求，任何满足条件的对偶变量赋值都给出原目标函数的一个上界或下界。本例中，有 10A + 5B + 15C ≤ 100y_N + 200y_S。

单纯形算法的最优字典给出，取值

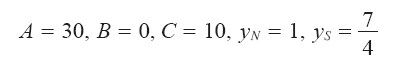
使上面的不等式两端均为450，这就证明了450是原目标函数的最优值，也是对偶目标函数的最优值。一举两得，花一道题的工夫，解出两道题的答案，多划算啊。

值得注意的是，对于任何线性规划题目，都存在这样简洁优美的最优性证明：单纯形算法构造出了用来相乘的系数，它们把线性规划原问题的约束条件合而为一，从而强有力地说明目标函数不可能取更大的值。进一步，这些系数本身又是线性规划对偶问题的最优解，而且原目标函数和对偶目标函数两者取值相等。这一美妙的结果称为强对偶性定理（strong duality theorem），最初由约翰·冯·诺依曼叙述并证明。²

^{2. 准确叙述为，如果一道线性规划问题与其对偶问题都有可行解，则它们都有最优解，且它们的目标函数最优值相等。}

强对偶性是线性规划问题里的重要理论，不过在TSP论题里，我们确实只需要更简单的命题，也就是弱对偶性定理（weak duality theorem）：在线性规划中，对偶问题的任意解都给出原目标函数的一个界。刚才几页草草掠过，许多细节浅尝辄止，你若错过了几处，也不必忧虑，下一节我们将针对TSP这种线性规划的特殊情形，直白易懂地解释，究竟何为对偶性，如何用线性不等式布下天罗地网，把旅行商团团围住。