5.7 整数规划

如果掌管线性规划的精灵出现，允许全世界的线性规划方法使用者许一个愿望，他们肯定会异口同声地祈求精灵赐给他们整数解。有一个原因显而易见，就是希望避免麻烦，比如要求生产33+1/3个产品的生产方案就相当棘手。但是，最主要的原因还是为了把决策归结为一系列独立的选择。是否应该建造一座新工厂？请回答“是”或者“不是”。是否应该生产销售一种新产品？请回答“是”或者“不是”。如果可以引入只能取值0或1、不能取分数或小数值的变量，那么线性规划模型就能给出这样的决策。这是线性规划的一类推广，它虽然威力强大，但是现阶段却离不开巨大的计算成本。

对变量附加整数限制之后，线性规划模型就不符合Dantzig的理论了，因此无法由单纯形算法或其他线性规划方法直接求解。尽管如此，成千上万人无法抗拒整数变量带来的灵活性，所以照样迎难而上，每天都在线性规划模型中使用这样的限制。这种拓展的模型称为整数规划（integer programming，简称IP）。

Dantzig最早做出了关于整数规划广泛适用性的书面记述。他的一篇论文同时为最优化理论和复杂性理论奠定了基础，其中也说明了如何将一长串重要的最优化问题逐一建模转化为整数规划问题。¹在1963年的线性规划专著中，他对这番研究工作作了如下的描述²：

^{1. Dantzig, G. B. 1960. Econometrica 28, 30–44.}

^{2. Dantzig (1963).}

我们的整体目标是对一些题目进行总结并分类，这些题能够归结为线性规划问题，而且其部分或者全部变量只取整数值。我们将说明，大量非线性、非凸性的组合问题虽然复杂困难，乃至表面看来完全无从下手，如今都有机会直接正面攻破。

他的题目分类包括TSP和最优地图染色问题。

染色问题是整数规划的典范应用实例。我们不考虑具体的地图，而是考察更一般的问题：对图的顶点染色，使得任意两个共边的顶点都不同色。我们在地图的任一区域内放入一个顶点，如果两个区域有公共边界，就在对应的两个顶点间连一条边，便可以把地图染色问题转化为上述一般的染色问题。

图5-19给出了一个用4种颜色染色的图。对于这一特例，不难看出，无法只用3种颜色给出符合要求的染色方案，但是一般而言，我们很难确定3种颜色够不够用。下面就把这种一般问题转化为整数规划问题。每个顶点i的颜色用3个非负变量x_i,red、x_i,green和x_i,blue表示。如果顶点i染成红色，那么令x_i,red取1，反之则取0，x_i,green和x_i,blue则分别对应绿色和蓝色，同样在0和1中间取值。因为顶点i的颜色必须指定为红绿蓝之一，所以有约束条件

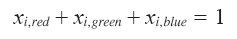
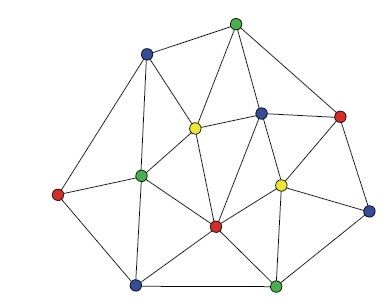
图5-19 用4种颜色染色

对于任意边（i, j），因为两端的顶点i和j不可能染成同一种颜色，所以有约束条件

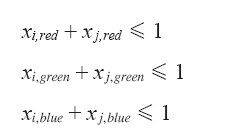
上面这组方程和不等式的整数解给出切实可行的红绿蓝染色方案。不过，如果不限制变量取值为整数，则令所有变量等于1/3也是满足条件的线性规划解，请注意，这个解完全不能提供任何对染色有用的信息。一切的意义都取决于整数变量。

5.7.1 TSP的整数规划模型

在某种意义上，我们已经成功建模，将TSP也视为一类整数规划问题。事实上，有了整数变量，再把度约束条件和子回路不等式结合起来，已经足够保证TSP题目的任何线性规划解都必定是一条完整回路。这个数学模型虽然属于整数规划模型，但并不能直接交给解题程序让它解决。问题在于，如果TSP题目包含n座城市，那么它的子回路不等式总数就近似等于2^n/2。

因此，Dantzig采用了另一种模型描述TSP题目，这次他使用了n³个非负变量，但约束条件只有n+n²个。模型的核心思想是，对于两个城市间的边，我们不仅标明它是否用在路线中，同时也标明它在路线中出现的顺序位置。Albert Tucker等其他早期TSP研究者曾经用过其他整数规划模型，那些模型变量和约束条件比这个模型更少，但是它们并不够切实可行，对旅行商用途不大，我们不打算耗费笔墨。迄今为止，所有其他模型在实际应用性能方面都不及子回路模型，也不如我们将在下一章介绍的方法。看到这些复杂的模型，你应该能够明白，要想从整体上解决整数规划问题很困难，因为多项式时间的整数规划解题程序就直接意味着多项式时间的TSP解题程序。

5.7.2 整数规划的求解程序

虽然解决一般性的整数规划问题是个难题，但世人并未因此却步，依然在海量商业应用中反复建立整数规划模型。就像面对TSP时一样，假如我们举手投降，向世界宣布，一般的整数规划问题也许压根不可能解决，那根本无济于事。我们必须用算法工程的方法攻克它。事实上，有人已经做到了，而这方面的成果大致就是TSP研究者的主要回报：几乎所有已知的整数规划问题通用解法，最初都是在求解TSP的过程中提出的。

至于全世界建立的商业整数规划模型，目前市面上有几种精巧复杂的求解程序正处在竞争之中。在过去20年间，这些计算机程序的实际性能获得了有力的提升，而放眼未来，我们会进一步了解如何打败旅行商（TSP）和整数规划（IP）这对兄弟，因此它们的求解程序必将迎来更大程度的改进。