9.4 TSP研究现状

Gerhard Woeginger在荷兰埃因霍芬理工大学工作，他也是克雷大奖的民间档案管理员，保管无数大胆的申领文件。他的“P与NP”网页的亮点在于，上面按照时间顺序列出了该问题的里程碑式成果，并在每条成果开始相应注明“相等”或“不相等”，例如¹。

^{1. 网站经过更新，2013年初，上面的序号44~46已变为47~49，特此说明。——译者注}

• [Not equal]: In September 2008, J. J. proved . . .
• [Not equal]: In October 2008, S. T. established . . .
• [Equal]: In November 2008, Z. A. proved . . .

翻译过来就是。

• [不相等]：2008年9月，J. J.证明了……
• [不相等]：2008年10月，S. T.证明了……
• [相等]：2008年11月，Z. A.证明了……

Woeginger提供了每篇论文的链接，有些时候还给出了反驳意见的链接。²有25篇论文支持“P=NP”，24篇论文支持“P≠NP”，双方可谓势均力敌，不相上下。读来有趣，可惜迄今为止，每篇论文都在严肃的审查面前败下阵来。

^{2. 参见http://www.win.tue.nl/∼gwoegi/P–versus-NP.htm。}

Woeginger的列表中，25条“相等”结果都是通过设计TSP变体问题的好算法得证的。这些方法五花八门，既有简单的枚举法，也有人不辞繁复，试图针对旅行商问题，构造出多项式时间的完整的线性规划方案。它们都有严重的漏洞，无一例外。不过，求解旅行商问题确实是证明P=NP的有望途径。

9.4.1 哈密顿回路

如果你准备向百万美元的大奖迈进，而你的计划中有一步是搜寻多项式时间的TSP算法，那么有必要牢记在心：只考虑有限定条件的TSP，足矣。很多人会选择研究哈密顿回路的判定问题，探究图中是否存在哈密顿回路的判定方法。我们知道，这道题是TSP的变体，也属于NP完全问题。不仅如此，如果假定输入的图是二分图（bipartite），该问题依然是NP完全问题。所谓二分图，即顶点可以分别染色为红蓝两色，使得每条边的两个顶点都为一红一蓝。具有如上限制的特殊结构可以用在算法中，但是要论多项式时间内解决的可能性，哈密顿回路问题其实不比完整TSP简单。

在此基础上，Alon Itai、Christos Papadimitriou和Jayme Szwarcfiter思考得更加深入。他们证明，可以具体说明哈密顿回路问题，把考虑的图限定为网格图（grid graph），即无穷网格的有穷子集。取一大片矩形网格，删去顶点的一个子集，就得到网格图，如图9-3所示。网格图为回路搜索算法提供了诱人的NP完全问题目标。David Johnson和Christos Papadimitriou称之为“TSP的终极特例”。¹

^{1. 见Lawler (1985)，“Computational Complexity”（计算复杂性）章节。}

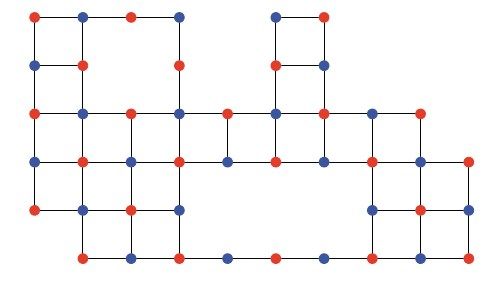
图9-3　网格图

9.4.2 几何问题

哈密顿回路问题清楚明白，没有枝节，不需要劳心计算旅行成本。可惜，对于我们多数人来说，为方便直观理解，TSP题目最好还是加以限定，使用欧几里得距离，以(x, y)坐标指明城市位置，以城市间直线距离作为旅行成本。解决这种TSP题目也能证明P=NP，收获百万美元的大奖。¹

^{1. 为理解该结论，注意到网格图上的哈密顿回路问题可以作为欧氏距离TSP求解。}

除了大奖难题以外，在同一背景下，还有另一个重要的问题悬而未决，而且乍一看令人意外：目前尚不知道，使用欧氏距离的TSP是否确实属于NP类。改用判定问题的方式来叙述，也就是问，指定数字K，是否存在长度至多为K的路线。因此，按照满足要求的路线顺序，列出所有城市，就构成了自然的证明。为简化数据显示问题，可以假定(x, y)坐标取值均为整数，则技术上的困难就在于计算平方根。近似计算每一个数的平方根都很简单，想算多少位都能轻松算出多少位，可是，把它们加起来就麻烦了，它们的和很可能距离K只差一丁点儿。要确定路线长度真的不大于K，就要算出足够精确的近似值。能否在多项式时间内做到这一点？目前尚无定论。

20世纪80年代初期，Ronald Graham普及了这道平方根之和问题。他举例说明了该题的困难之处：下面有两行数，每个都加上1 000 000，然后分别取它们的平方根之和。

1 25 31 84 87 134 158 182 198

2 18 42 66 113 116 169 175 199

例如，由第一行得到的和是√1000001+ √1000025 +. . .+ √1000198。看起来平淡无奇，可是算完就会发现，得到的两个值分别为

9000.4499835688397309490268288613590291912

9000.4499835688397309490268288613590291915

两者直到小数点后第37位才首次出现差别！一般说来，目前仍不清楚，要确定一系列平方根之和是否不大于给定数K，多项式量级的数字位数是否够用。具体到欧氏距离TSP的例子里，输入的规模是K和各个(x, y)坐标的数字位数。

解决平方根之和问题，便可长驱直入，直接证明欧氏距离TSP属于NP问题。不过，要证明一组点有长度至多为K的周游路线，这不是唯一途径，或许还有其他方式，只不过需要借助尚不为人所知的几何结构。这方面的研究很有意思。至少就TSP而言，这也许比平方根之和所需的数论方法更值得研究。

9.4.3 Held-Karp纪录

要想确定旅行商问题在多项式时间内能否解决，不管是给出肯定答案还是否定答案，大概都需要有颠覆性的革新思想才能做到。不过，另一个目标没那么困难：反复改进TSP算法最知名的运行时间界限，一点一点瓦解问题的复杂性。这种逐步方法自有其诱人之处，毕竟如果算法能获得更快的时间界限，就可能适用于实际应用，从而推进TSP的实战前线。

“没有最快，只有更快”确实是复杂性分析的座右铭。但是在TSP领域，似乎早在1962年，研究者就遇到了无法翻越的高峰——Michael Held和Richard Karp的研究成果¹。他们的动态规划算法能在正比于n²2ⁿ的时间内，解决任何一道n座城市的TSP题目。时至50年后的今日，境况依然如此。要超越Held-Karp纪录，或许不需要“革命”那么夸张，但显然需要令人眼前一亮的创新。

^{1. Held和Karp (1962).}

鉴于Held和Karp是最高纪录保持者，不完整介绍一下他们的算法，实在是说不过去。为方便解说，考虑n座城市的TSP题目，城市从1到n依次编号命名，每两座城市之间的旅行成本记为cost(1, 2), cost(1, 3), 等等。

固定城市1作为旅行社的出发地，Held-Karp解法根据最优子通路得到解，而最优子通路则分别针对不包含城市1的每个城市子集和其中每个终点得出。以子集{2, 3, 4, 5, 6}为例，若选取6为终点，则所谓最优子通路需要满足：从城市1出发，到城市6结束，按任意顺序经过城市2、3、4、5，并且是所有此类通路中成本最低的。这样一条最优子通路的旅行成本记为trip({2, 3, 4, 5, 6}, 6)。为计算该值，求和式

trip({2, 3, 4, 5}, 2) + cost(2,6)

trip({2, 3, 4, 5}, 3) +cost(3,6)

trip({2, 3, 4, 5}, 4) +cost(4,6)

trip({2, 3, 4, 5}, 5) +cost(5,6)

中的最小值，这四个和分别对应子通路中倒数第二座城市的四种选择方式，即转化为首先按最优路线前往倒数第二座城市，然后再从那里出发前往城市6。

从若干个关于四座城市的数值出发，构造关于五座城市的trip值，正是Held-Karp方法的核心所在。该算法如下进行。第一步，计算所有关于一座城市的数值。这很容易，例如trip({2}, 2)就是cost(1, 2)而已。第二步，使用关于一座城市的数值，计算所有关于两座城市的数值。第三步，使用关于两座城市的数值，再计算所有关于三座城市的数值。以此类推，最后得到(n-1)座城市的数值时，即可直接读出最优路线的成本，因为在和式

trip({2,3,. . . , n}, 2) +cost(2,1)

trip({2,3,. . . , n}, 2) + cost(2,1)

trip({2,3,. . . , n}, 3) +cost(3,1)

…

trip({2,3,. . . , n}, n) +cost(n,1)

中，cost项对应于返回城市1的路程，所以最小值就是所求结果。

原理就这么简单，介绍完了。下面推算运行时间界限。首先，在n座城市的题目里，有2^n-1个不包含起点的城市子集，这是基本事实。在每一个子集里，终点至多有n种取法（事实上，取法数目只是相应子集的基数，但是为方便计算，此处统一增加到最大值n），trip值计算过程包括少于n次加法和少于n次比较大小。2^n-1乘以n再乘以2n，可知总步骤数不会超过n²2ⁿ。

只要城市数目n超过10，那么上述运行时间界限就比枚举检验所有路线更好。但假如这个Keld-Harp结果就是最好结果，难免让人灰心丧气。在尝试突破纪录时，挑战者应当把重点放在2ⁿ项上。即使把n²2ⁿ改进为n²ⁿ，也不能算是重要提升；但一旦改进为n²(1.99)ⁿ或者n²2^√n，就堪称重大新闻，甚至可能标志着新时代的开端，其后的新改进可能带来更好的实用方法，具有强有力的运行时间保证。²

^{2. 此类研究的优秀参考资料见：Woeginger, G. J. 2003. Lect. Notes Comp. Sci. 2570, 185-207.}

9.4.4 割平面

若想打败Held-Karp，何不试试割平面法？Randall Munroe是xkcd.com的作者（画手）兼创始人，第1章的图1-5就是出自他笔下的TSP漫画。在发布该画作时，他的评论正中要害：“最好的线性规划割平面方法，属于哪个复杂度类呢？我遍寻而不得答案。嗨，画加菲猫的那哥们儿可不会碰到这种问题。”¹

^{1. 请访问Randall Munroe的网站xkcd.com，在编号为399的TSP漫画上方悬停鼠标，就能看到这一评论。}

割平面法是当之无愧的实际计算冠军，所以当然可以考虑把它用在TSP的复杂性分析中。

可惜，割平面法在最差情形下的性能如何，似乎不容易一窥究竟。1987年，我和Vašek Chvátal、Mark Hartmann共同证明，分支切割法有一种强的形式，需要至少2^(n/72)/n²步操作，才能解决哈密顿回路问题的一道专门构造的棘手题目，而其他TSP题目甚至可能需要更多的步骤。不过该分析并未封杀所有可能性，新类型的割平面仍有可能大大改进运行时间界限。当前，人们正在搜寻性能更佳的分支切割法实现，而搜寻新的割平面恰是不错的理论目标，两者完全可以相辅相成，同步进行。

9.4.5 近优路线

一旦证明P≠NP，对于好的TSP算法便无需再抱任何希望。幸好，旅行商尚有一线生机。例如，第4章描述了Nicos Christofides提出的基于树的启发式算法，它保证能给出成本不超过最优路线之1.5倍的路线。假如能够改进这一结果，得到1.01倍的近似算法，保证给出与最优解之差小于1%的路线，又将如何？届时，该算法的快速计算机实现会成为许多相关应用的得力工具，用途超乎想象。

即便无法用来确定P与NP问题的结论，这样的近似算法必定代表了一条值得探究的路子。然而，为研究它们，就必须限制旅行成本的取值范围，排除困难的“是/非”判定问题。¹Christofides本人的做法也就是通用标准做法：假定旅行成本是对称的，而且满足三角不等式，即对于任意3座城市A、B、C，从A到B和从B到C的旅行成本之和不能小于直接从A到C的旅行成本。满足这种自然条件的题目则称为TSP的度量（metric）题目。

^{1. 一般的哈密顿回路问题可以成功编码，方法是在图中存在对应边的各对城市之间的旅行成本都赋值为0，不存在的各对城市之间成本赋值为1。则哈密顿回路的成本为0，非最优解的路线成本均至少为1。因此，如果存在某种方法，对于任意给定的近优路线与最优路线之间误差百分比要求，都能返回符合要求的近优解，那么这种方法就能为“是/非”问题提供答案。}

Christofides算法最早出现在卡耐基梅隆大学的一篇论文里。当时是1976年，他的结果似乎相当简单。可是30年过去了，一直没有改进，可见他的结果并没那么简单。确实，要找到多项式时间的α倍近似算法，满足α小于1.5且适用于一切度量题目，仍是亟待解决的难题。

公平公正地说一句，有必要指出，其实也许根本不可能超越Christofides。支持这一消极论点的依据是，Christos Papadimitriou和Santosh Vempala业已证明，除非P=NP，否则没有多项式时间的α倍近似算法能解决TSP的度量题目且满足α小于1.0045²。因此，他们的研究扼杀了在P≠NP时获得极好近似算法的幻想。真正的计算壁垒在哪儿？更接近1.0045还是更接近1.5？没人知道。没法缩小这一范围固然使人不爽，不过有趣的未解研究课题列表上面可以再添一项了。

^{2. 准确值是220/219。}

9.4.6 Arora定理

普林斯顿大学的Sanjeev Arora证明了一个重要定理，既揭示了近似方法的愿景，也揭露了它的陷阱。他证明，无论选取怎样的α值，只要超过1.0，就存在适用于欧氏距离TSP的多项式时间α倍近似算法。¹注意欧氏距离的情形与度量情形不同，后者除非存在计算最优路线的多项式时间算法，否则根本不能指望这么好的结果。这是Arora定理的乐观一面，很有意思，表明欧氏距离的TSP可能比一般的度量题目更容易搞定。

^{1. Arora, S. 1998. J. ACM 45, 753–782. 另参见：Mitchell, J. 1999. SIAM J. Computing 28, 1298–12309.}

下面指出近似方法的陷阱。虽然Arora定理是出色的理论结论，但当α值接近1.0时，近似算法的运行时间却会显著增长，实验结果更是很不理想。其实，近似方法一贯如此，因为要获得高质量的解，就需要非常精细地划分空间，同时还要以延长搜索时间为代价。要把Arora的几何方法巧妙转化为实际TSP工具，还有待后人出手解决。