4.4 借鉴物理和生物思想
事实证明,把TSP视为一类搜索问题的特例,从全局着眼看待寻找路线过程,这种出发点无论对于找到好的路线还是想出多用途的技术都大有裨益。思路意图在于产生元启发式算法(metaheuristic),即用来设计启发式算法的启发式算法。这类研究工作本质具有一般性,因此科学界各领域的研究者纷纷前来参与搜寻路线之旅。
4.4.1 局部搜索与爬山算法
该研究领域中有一个类比很有价值:想象路线所处环境具有一定的地形变化,每条路线的高程对应于它的好坏程度。脑海中的图像恰似加舒尔布鲁木诸峰,如图4-24所示,好的路线对应于各座山头,而最好的路线位于高耸入云的加舒尔布鲁木II峰之巅。这样一来,启发式算法就可以想象成四处移动搜寻高地的过程。

图4-24 加舒尔布鲁木诸峰(Florian Ederer供图)
为使这种想象图景有意义,应当对两条路线在什么情况下彼此相邻加以说明。通常的处理方法是在每条路线周围设定邻域(neighborhood)。例如,可以把两条路线相邻定义为它们能够通过一步2-交换操作互相转化,或者定义为能够通过LK算法找到的某种交换操作互相转化。大的邻域有助于在地理环境中确定前进方向,而构建邻域时应当使算法能查看并评估近邻。
爬山算法(hill-climbing algorithm)代指一类路线改进方法,以反复操作改进性的2-交换为例。这类算法之所以得名,是由于其过程可视为沿一系列相邻路线前进,始终向高处移动。算法的每一步都进行一次局部搜索(local search),以寻找附近的高地。若搜索全面彻底,则最终算法将在山峰上终止,或者至少在高原上终止,因为此时所有局部移动必然要么走下坡路,要么走平路。完整运行时,算法会从初始路线出发,然后迅猛攀升到局部高峰处。
请注意,初始路线的选取将决定爬山算法的命运:如果初始路线只能到达小山坡的半山腰处,那么算法就会受到局限,最终路线将会表现平平,只能登顶那座小山而已。 因此,Lin和Kernighan决定选择随机路线作为反复运行LK算法的初始路线。理由何在?想象向所处地面投掷飞镖,若飞镖数量足够多,便有很大概率击中高峰周围的山坡。
随机路线可以使飞镖落点广泛分散开,但是也有缺点,就是它们通常不是好路线,所以初始阶段往往会在低洼的山谷中蜿蜒很久。如果TSP题目的规模很大,从山谷走到山峰就可能需要很长时间。也可以选择折中的方法,通过随机选择出发城市保证路线的随机性,再按照最近邻原则投掷飞镖。
4.4.2 模拟退火算法
模拟退火(simulated annealing)算法是一种启发式算法。它按照一定概率接受比当前解更差的邻域,因此条件限制比爬山算法更弱。这种情况下的接受概率一开始比较高,然后随着算法运行而逐渐降低,使算法有机会先跳到更高的山坡上,然后才转而稳步向上攀登。
模拟退火算法由Scott Kirkpatrick、Daniel Gelatt和Mario Vecchi发明。他们的原始论文研究了TSP,并针对一道400座城市的题目公布了启发式算法得到的若干路线。1他们写道,该方法的动力源于统计力学与TSP的关联,在统计力学中,退火表示先加热再缓慢冷却材料以改善其结构的工艺过程。
1. Kirkpatrick, G., C. D. Gelatt, M. P. Vecchi. 1983. Science 220, 671–680.
迄今为止,模拟退火算法尚未给旅行商带来多少好处,但它作为通用搜索方法却获得了盛大的成功。谷歌学术搜索数据表明,原始论文引用次数超过18 700次,这样的引用率几乎是前所未有的。
4.4.3 链式局部最优化
模拟退火算法给当前的寻找路线方法带来的最大影响很可能不在于这种方法本身,而在于它向TSP研究领域引入了物理学的思想。事实上,计算结果之所以能够首次突破反复LK算法所能达到的界限,应当归功于物理学家的跨界贡献。
20世纪80年代末,加州理工学院物理系的Olivier Martin、Steve Otto和Edward Felten三人提出了不同于“投掷飞镖”随机策略的另一种方法。他们的想法是,像LK算法这样强大的局部搜索算法得到的路线往往会延伸到所处区域内的高地,因此可以对这一点加以利用。于是,Martin等人提议,算法第二次运行时不再从随机城市出发,而是首先观察当前所处的山峰周围,判断能否越过附近的几处壁垒,到达通向更好地点的另外一座山坡上。
具体的方案是通过变换原有的LK路线获得一条新的初始路线,而不是随机投掷飞镖确定。算法全过程多次重复这一变换步骤,一发现更好的路线就用它替换原有路线。要想使算法有效运作,路线在变换后必须离开原有邻域,因此这种改动难以通过LK算法还原。Martin等人发现,如图4-25所示类型的随机4-交换就可以圆满完成任务。
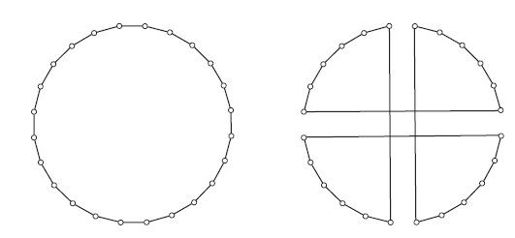
图4-25 双桥变换
这样得到的算法性能出色,称为链式Lin-Kernighan算法(Chained Lin-Kernighan),即链式LK算法。这种思想之所以成功,得益于种种机缘巧合。首先,Martin等人的直觉是正确的,通过kick机制访问邻近区域确实可以更好地认识周围山峰的情况,LK算法本身则用来引领路线在山坡上爬升;其次,路线经过变换后,运行LK算法的速度确实比随机路线快得多,原因很简单,毕竟变换后的路线大体形状比较好,所以算法无需多次迭代即可获得局部最优解。
链式LK算法的程序实现基本上垄断了20世纪90年代的路线搜寻领域。Concorde程序就用到了该算法的一个版本,对于城市至多可达100 000的题目,通常也只需一两秒便可找到超出最优解不到1%的路线。若想获得更好的解,可以选择使用LKH算法。然而如果题目的数据集非常大,那么链式LK算法依然占据统治地位。例如,有一道题目包含25 000 000座城市,各点落在25 000 000×25 000 000的正方形内,横纵坐标均为整数,路线数据取为欧几里得距离,计算结果如图4-26的曲线所示。2000年的计算机在8天时间内找到了一条路线,其长度大约比最优路线长0.3%。1
1. Applegate, D., W. Cook, A. Rohe. 2003. INFORMS J. Comput. 15, 82–92.
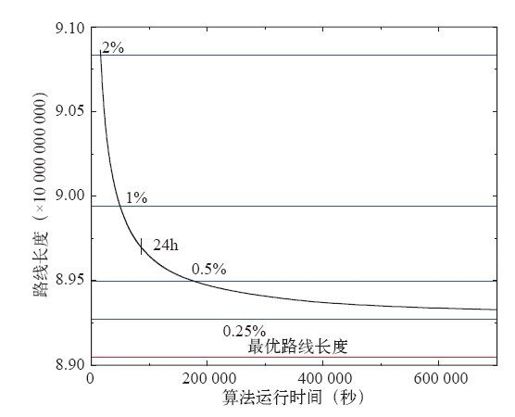
图4-26 应用链式LK算法求解一道题目的情况,该题包含25 000 000座城市,数据取欧几里得距离
4.4.4 遗传算法
有人如上所述,以地理思路看待旅行商路线,也有人从生物角度出发,把路线当成能够逐渐变异和进化的生命有机体。有一类算法应用了后一种思维方式,称为遗传算法(genetic algorithm),其灵感来源是John Holland出版于1975年的里程碑式著作Adaptation in Natural and Artificial Systems(《自然系统与人工系统中的适应性》)。1Holland并未讨论如何解决TSP,但不久后,他的遗传算法思想便出现在寻找路线的文献中。
1. Hollan, J. 1975. Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor, Michigan.
在TSP领域,遗传算法的思路大致如下。首先形成路线的初始“种群”,可以通过反复从随机城市出发使用最近邻算法获取路线。然后是一般的循环步骤,在种群中选取若干对路线,让它们“交配”(即交叉配对)得到子代路线2,再从父子两代路线中选出一个新的种群。反复多次进行这一步骤,最优秀的路线最终将脱颖而出,成为唯一的生存赢家。
2. 针对其他类型问题的遗传算法时常还有一步“变异”步骤,即种群的个体发生突变。
遗传算法的实质是模拟自然界的进化过程。类比饶有趣味,但请牢记在心,仅仅借用达尔文的语言并不意味着最终一定能得到好的路线。事实上,早期的TSP遗传算法并无可圈可点之处,即便题目规模限制得非常小,结果也不太出色。然而,维持路线的种群这一想法具有明显的优势。根据一般性的遗传算法,可以精心设计出威力强大的启发式算法,结合局部搜索方法使用则效果更佳。
在遗传算法的基本原则框架下,路线种群进化的方法各式各样,为我们留有充足的选择空间。我们不但可以选择交叉配对过程,也可以选择适应度评价标准(fitness measure)以确定如何选取下一代种群。关于这一评价标准,人们提出了一些绝妙的思路,力求在解的品质和种群的差异性之间达到最佳平衡。
就交叉配对过程本身而言,早期的遗传算法方案试图在一条父代路线中搜寻能够被另一条父代路线的子路线替换的部分子路线。这种做法限制性很强,题目规模较大时尤甚。另外一种做法则更有效,即对于两条父代路线A和B,在A中选择一段子路线,然后尽量选择B和A的边(优先选择B的边),把它扩充为完整路线。还有一种配对方法如图4-27所示,称为边交叉(edge-assembly crossover,简称EAX)算法。图中有两条环游美国的路线,分别染成蓝色和红色。为了将两者组合到一起,我们取它们包含的边的并集,并在相应的图中选取一条各边颜色红蓝交替的回路,如图4-27中小图(3)所示。然后,我们考虑原来的蓝色路线,删去出现在新回路中的蓝边,再添加上新回路中的红边,如小图(4)所示。最后,我们通过一步2-交换操作,把上述过程中产生的子路线合并为一条完整路线,如小图(5)和(6)所示。
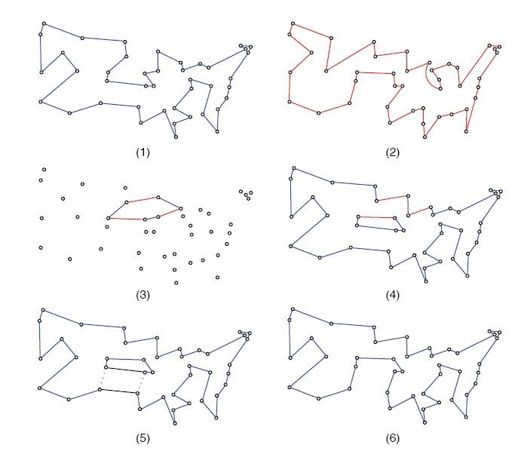
图4-27 两条路线交叉配对
永田裕一采用EAX配对方案,发明了一种卓有成效的寻找路线方法,时至今日仍鲜有敌手。3该算法的实现以EAX的超高速实现为基础,可以连续处理多代路线。他成绩斐然,比如他为100 000座城市的《蒙娜丽莎》一笔画TSP找到的路线就是目前已知最好的一条。
3. Nagata, Y. 2006. Lect. Notes Comput. Sci. 4193, 372–381.
4.4.5 蚁群算法
也许读者曾经遇到过这样的情景:自己的食物不幸落入一群饥肠辘辘的蚂蚁的口中。这群讨厌的小虫通常排成一条长队,浩浩荡荡向你的花园甚至室内进军。一只蚂蚁单独行动时并无章法可言,但是整个蚁群通过信息素轨迹相互交流,却能成功找到省时省力的路线。受到蚂蚁集体行为的启发,一类TSP启发式算法诞生了,这就是蚁群优化算法(ant-colony optimization,简称ACO)。
蚁群算法研究的领军人物是比利时人Marco Dorigo。1992年,他在博士毕业论文里提出了该算法的思想。1此类算法的工作原理是令一小群蚂蚁沿着图的各边移动,每只蚂蚁探寻一条路线,每次到达新顶点时都选择一条通向未访问过的顶点的边。选择规则是算法的核心,选择的依据是每条边对应的信息素值(pheromone value),信息素值高则选中概率也高。等到所有蚂蚁都走完路线后,各边的信息素值会根据一定的规则变化,增量与路线长度成正比,因此好路线各边的信息素值增加程度大于坏路线的边。
1. http://www.aco-metaheuristic.org.

图4-28 求解TSP的蚂蚁(Günter Wallner供图,原图出自Georg Glaeser和Konrad Polthier的著作Bilder der Mathematik一书)
这种方法自然直观,令人心动,然而它至今未表现出与改进的LK算法一较高下的能力。不过,最近几年间,ACO算法在其他领域大显身手,有效解决了诸如时序安排问题、图着色问题、分类问题和蛋白质折叠问题等形形色色的难题。这个活跃的研究题目有力地佐证了对旅行商的关注如何能给研究者指明方向,使他们发现有趣的通用方法,可以求解具有各式各样的应用背景的最优化问题。
4.4.6 其他
TSP的各种元启发式思想得到了大量运用,本节只述及了其中性能最优秀的几种,还有许多其他方案,如神经网络算法(neural network)、禁忌搜索算法(tabu search)和人工蜂群算法(honey bee)。如果你想到了一种通用的搜索机制,那么在开发、改进、测试及比较这种新方法时,即使你预想的应用领域与小小旅行商的奔波路线相去甚远,TSP也是非常合适的练兵场。
