2.5 统计学观点

在数学界，常常有各路人马研究同一个重要问题，有时研究小组之间并无交流，都以为自己是在孤军奋战。旅行商问题也不例外。当时在美国，Flood和兰德公司都在奋力求解TSP。与此同时，在地球的另一端，统计学家Prasanta Chandra Mahalanobis也开始研究这个问题。但Mahalanobis的数学观点别具匠心，关心的实际应用问题也与美国研究者截然不同。

2.5.1 孟加拉黄麻农田

Mahalanobis成立了印度中央统计局，创办了统计学期刊Sankhya，被誉为印度的统计学之父。他的一个主要研究方向是抽样调查的技术方法，并在此领域与TSP结下了不解之缘。

20世纪30年代，黄麻作物是印度政府财政收入的重要来源，大约占到出口总额的四分之一。当时，黄麻种植地主要分布在孟加拉地区¹。如何收集数据以准确预测黄麻产量是实际生产中的一大问题。

_{1. 当时孟加拉地区遭受英国殖民统治，是英属印度的一个省。——译者注}

由于当时黄麻种植分散，孟加拉地区总共有大约600万处小农田生产黄麻，因此要想完全调查每一处黄麻田是不现实的。Mahalanobis提出了一个替代方案：随机抽样调查，把孟加拉地区分成多个区域，各个区域内的田地性质都差不多，在每个区域随机选一些点观察黄麻的种植情况即可。抽样调查需要花费时间和金钱，成本的主要影响因素就是在不同样本区域之间运送人和设备的时间。从这个方面来看，这个问题就变成了一道TSP，要寻找连接所有选定农田地点的高效路线。就此，Mahalanobis在1940年的一篇研究报告里写了下面这段话^[2]：

_{2. Mahalanobis (1940).}

很容易大致了解旅行的情况。首先假设在任意地区内都随机分布着n个样本单位，每个样本单位都可以看成一个几何学上的点³。再假定在两个样本点之间移动时，可以安排路线使总路程尽可能小，换言之，在任意两个样本点之间都沿直线移动。如此一来，容易知道，任意两个样本点之间的路程的数学期望是√n−1/√n，所以我们从一处样本田去往另一处的花费就正比于√n−1/√n。如果n比较大，也就是说，我们考虑的地区面积相当大，那么从一处样本田去往另一处所需的时间将近似正比于√n，这里n是给定地区内的样本总数。

_{3. 在几何学中，点只有位置，没有大小和形状。——译者注}

什么是期望？如果我们每次都随机取n个点并求解对应的TSP题目，那么经过多次重复试验，最优路线的平均长度就是期望。也许因为Mahalanobis是一位统计学家，他的研究兴趣在于统计学领域，所以他并没有讨论实际操作任务，换言之，没有对于具体数据真正求出路线，而是关注最优路线长度的统计估计结果。与普林斯顿大学和兰德公司的研究方向相比，这种视角可谓独树一帜。

在计算孟加拉地区抽样调查的预计成本时，Mahalanobis提出的估计值派上了用场。1937年，人们进行了一次小型试验，并在次年实施了大规模的调查。在做出这些决定的过程中，预计成本都是非常重要的考虑因素。

图2-19　Prasanta Chandra Mahalanobis（左）和Mahalanobis在进行田间抽样调查（右）。（印度中央统计局Mahalanobis博物馆供图）

2.5.2 证实路线估计值

Mahalanobis给出了一个TSP公式，却并没有给出严谨明确的分析过程。不过，他的研究工作给统计学界的后来人指明了前进的方向，确立了研究的目标。每一个点的坐标设为(x, y)，其中x和y分别等可能地取0到1之间的任意数值，像这样的分布称为随机分布。统计学家想要进一步了解的问题就是，当单位正方形内随机分布的城市数目增多时，TSP路线会如何增长。具体说来，他们想求出周游这个点集的最优路线长度满足什么公式。

研究者在两个方向分别取得了进展。1948年，Eli Marks证明了周游一组随机点的最优路线长度的期望不小于(√n-1/√n)/√2；1949年，M. N. Ghosh证明了期望长度至多不超过1.27√n。当n很大时，综合以上两个结果便证实了Mahalanobis的直觉，路线长度的期望值确确实实正比于√n。

Ghosh在论文里给出了期望的上界，并且特意对根据具体数据实际计算结果的工作发表了评论。“在地图中选定该区域的n个随机分布的点以后，很难真正实际找出连接所有点的最短路线，除非n非常小。而在大规模调查中，几乎不可能出现很小的n。”¹

_{1. Ghosh, M. N. 1949. Calcutta Stat. Assoc. 2, 83–87.}

有趣的是，Ghosh也发现了TSP的真正困难之处在于找出最优路线，但是他显然没有受到Menger、Whitney和Flood的影响，而是独立得出了这个结论。

2.5.3 TSP常数

综合Mahalanobis、Marks、Ghosh三人的结论，我们可以对平均路线长度做出估计，但是无法从估计值中看出一系列试验所得长度的分布范围，因为有些试验的随机点集可能给出很长的最优路线，有些则可能很短。不过如果n充分大，那么这种偏差很大的现象并不会出现。图2-20的柱状图可以帮助理解这一结论。对1000个点的情形，进行10 000次随机取点试验，把每次的最优路线长度除以√1000就得到了图中纵坐标的数值。所有试验值形成了一条优美的钟形曲线，正中间的均值是0.7313。在这幅图中只有1000座城市，所以有些路线长度值会有一定程度的偏离。但是根据Beardwood、Halton、Hammersley于1959年提出的著名理论，可以得知，如果n增大，则长度数值分布会以特定的β为中心形成狭窄的峰形¹，β称为TSP常数（TSP constant）。

_{1. 结论为，如果n增大，则最优路线长度除以√n的值会以概率1收敛到β。Beardwood, J., J. H. Halton, J. M. Hammersley. 1959. P. Camb. Philos. Soc. 55, 299–327.}

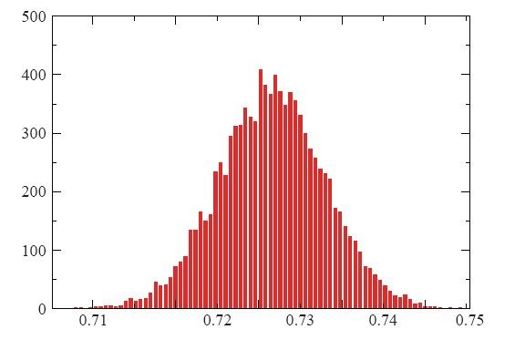
图2-20　对于1000个点的情形进行10 000次试验的路线长度分布图

确定TSP常数β的值是一个很有吸引力的挑战，这方面的研究也为概率论带来了重要的新分支学科。但是现有的结果都只是近似值，要想确定真实值依然有很远的路要走。所以现状是，我们知道一个自然常数，却不知道它的真实值。

David Applegate、David Johnson、Neil Sloane正在研究β。他们的工作已经解决了6亿多道几何情形的TSP题目。解题过程中，Concorde也得到了充分的锻炼。尽管只凭一大堆计算结果并不足以证明任何确定的结论，但是得到的数据曲线（例如图2-21）都强烈表明，当n增大时，平均路线长度除以√n的数值会持续下降，最终趋于固定值β，近似为0.712。²

_{2. 物理学家也对β进行了耐人寻味的研究，参见：Percus, A. G., O. C. Martin. 1996. Phys. Rev. Let. 76, 1188–1191.}

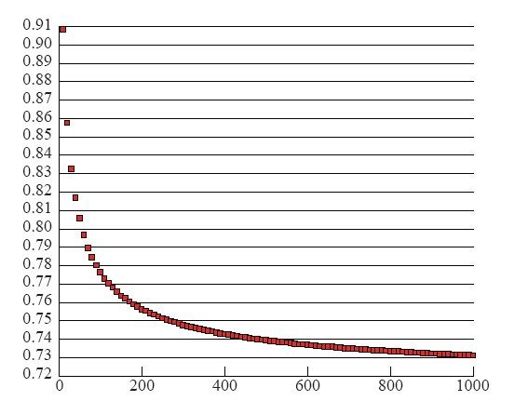
图2-21　平均路线长度与n的关系图，其中每个点都为10 000次试验的平均值