3.1 公路旅行

本章将综述TSP的应用，首先介绍一些实际的旅行事例，当然也包括旅行商的旅行。

3.1.1 数字化时代的推销员

如今，各地区的巡回推销员出行时，一般会驾驶配有GPS（全球定位系统）的汽车。在车载GPS使用的地图软件中，常常包含一个小程序，能够求解十几个城市的小规模TSP。这个数目往往已经足够满足单日出行的需要了。GPS设备里存有详细的地图，从而能够准确地估计从某地去往另一地所需的时间，因此TSP的解便可以反映出实际面临的行车条件。

普林斯顿大学的Alain Kornhauser是地图制图技术应用方面的专家。他介绍了GPS设备的一种有趣的反向用途。使用者在GPS上按照精度和纬度设定目的地之后，有时候会发现这个点不可能落在已知的道路区域内，也就是说根本没有路可以到达那里。但是如果当地的货车司机必须把货物送到，他往往能找到一条路成功抵达目的地，比如抄一条地图上没有标注的小路。这种情况下，GPS系统就把信息报告给中心服务器，然后服务器就在相应的地图坐标格里，沿着货车经过的路径，加上一条新的连接线。于是下一次有人要去同一个地点送货的时候，地图软件就可以用到这条新添加的路了。

3.1.2 取货与送货

人们常常用小规模的TSP模型来规划客车接送乘客或者货车配送货物的路线。Merrill Flood曾经写道，当初是一道校车路线问题引领他走上了TSP研究的道路。伦敦政治经济学院的George Morton和Ailsa Land组成了另一个早期的研究小组，他们对TSP的兴趣则来源于一道洗衣店送货的题目。Rapidis公司开始的时间更晚一些。该公司之所以使用Concorde程序，是为了给客户规划路线。他们的客户是广告材料样品分发商Forbruger-Kontakt公司，其业务范围包括丹麦等多个国家。Rapidis公司开发了一款路线规划软件，图3-1就是根据该软件的屏幕截图而画成的。图中的路线需要遵守单行道之类的行车限制，因此在两地点间来回的花费与方向也有关系。

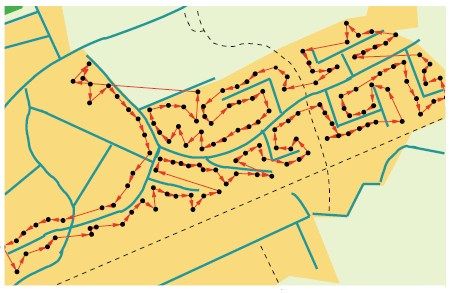
图3-1　Forbruger-Kontakt公司送货的TSP路线（Thomas Isrealsen供图）

3.1.3 送餐到家

佐治亚理工学院的一个研究小组介绍了TSP算法的成功应用案例。在美国亚特兰大市的“送餐到家”（Meals on Wheels）服务项目中，该研究组用一种快速启发式算法为送餐工作人员构建路线。¹该项目每天要把饭送到大约200个地点，其中每一名司机配送的地点在30到40之间。为了构建司机的行车路线，研究者首先将所有200个地点连成一条路线，然后再把这条总路线分成长度合适的小段路线。借助如图3-2所示的空间填充曲线，可以得到总路线。如果让空间填充曲线的结构变得越来越精细，那么最终城市内任意一点都将落在这条曲线上。按照曲线经过各点的顺序，把200个不同地点排起来，就得到这条启发式路线。

_{1 “送餐到家”是一种社会服务项目，志愿者为老年人及行动不便者提供午餐并负责配送上门。参见：Bartholdi III, J. J., et al. 1983. Interfaces 13, No. 3, 1-8.}

这种构造路线的方法操作简单，因此容易更新维护。如果有新的客户加入或者原来的客户离开，项目管理者可以轻而易举地手动更新路线，下面简单介绍一下他的做法。首先，一个地点在空间填充曲线上的相对位置θ完全决定了它在路线中的次序，所以佐治亚理工学院的研究小组就先对地图上密密麻麻的小格预先计算好θ值，这些小格也就是位于亚特兰大标准地图不同坐标(x, y)处的地点。然后管理者把当前参与项目的客户名单储存在两套索引卡上，第一套按姓名首字母顺序排列，第二套则按照路线中所处的次序排列，也就是按照θ从小到大排列。这样一来，如果想要去掉一个客户，只需要抽出相应的两张卡片即可；如果想要新增加一个客户，则对照地图确定新客户位置对应的(x, y)坐标，然后在计算出来的θ值表格里查找相应的θ值，从而确定新客户在路线中的次序并把其卡片插入第二套卡片中。对于这道TSP实际应用题，他们的解法不需要借助高科技，实在是巧妙至极。

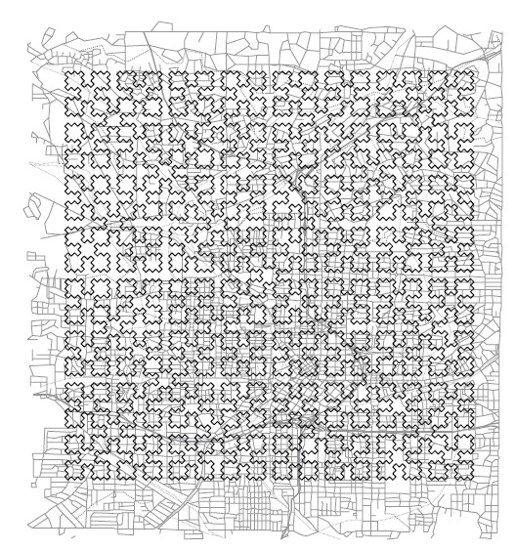
图3-2　亚特兰大地区的空间填充曲线（John Bartholdi供图）

3.1.4 农场、油田、蓝蟹

TSP可以用于规划另一类路线，就是检查、视察相距较远的地区。此类后勤组织应用以Mahalanobis在20世纪30年代的农业研究为早期实例，不过也可以用于其他情况。William Pulleyblank在论文中介绍了一例。题目背景是为油田规划路线，总共到达尼日利亚的47个海上采油平台，而乘坐的直升机要从陆上基地起飞，最后TSP软件解得了所求路线。马里兰大学的一个研究小组则提供了另一例。这道问题是关于乘船出海的。他们需要到达美国切萨皮克湾的大约200个监测站，以监测海湾内的蓝蟹数量，结果遇到了困难，由于每次出海时间太长，没法完成对所有检测站的高密度监测。因此他们转向TSP模型求助，解决了路线规划问题。

3.1.5 巡回售书

小说《毗湿奴之死》（The Death of Vishnu）的作者Manil Suri是一名数学教授。他在SIAM News发表了以下感想¹。

_{1 Suri, M. 2001. SIAM News 34, p. 1.}

我在美国的首轮巡回售书将从2001年1月24日开始，历时三周，总共要去13座城市。出版社给我城市列表的时候，我发现这简直是太神奇了！我自己要亲身体验旅行商问题了！我竭力把内心的激动之情传达给出版社的宣传部，努力向他们描述这一切在数学上有多么重要，我们要怎么做才可能得出一个最优解，如此等等。我的狂热弄得他们很不自在。他们告诉我，他们在规划巡回路线方面经验丰富，要我放心，还说如果需要数学上的帮助的话，他们会再和我联系。至今，他们也没有找我。

尽管Suri的出版商对此全无热情，但巡回售书作为TSP的背景问题确实非常自然。

3.1.6 “多走一里路”

虽说 “多走一里路”俱乐部（Extra Miler Club）的座右铭是“因为两点之间的最短距离太没劲”¹，不过他们的会员以周游美国全部3100多个县（郡）为目标，而且确实喜欢规划路线。严格说来，这算不上TSP，因为只要进入县的边境线就算到过这个县，不过也有一些会员认为要到政府所在地才真正算数。

_{1 该俱乐部位于美国，会员多数以驾驶机动车周游全国为目标。在英文中，“多走一里路”（extra mile）指超出别人期许，多付出一些努力，出自圣经马太福音：“有人强逼你走一里路，你就同他走二里。”——译者注}

据《华尔街日报》报道，“多走一里路”俱乐部有一名会员的目标是到北美的每一家麦当劳吃一个巨无霸，总共有13 000多家店。²这本来是个不错的TSP实例，可惜俱乐部官方网站介绍说，这位会员“现在已经向着饕餮难度更低的目标出发了”。

_{2 Dosher, M. Wall Street Journal, 1998-02-09, B1.}

3.1.7 摩托车拉力赛

“多走一里路”俱乐部的会员通常开汽车出行，而铁臀摩托车协会（Iron Butt Association）则流行选择摩托车作为交通工具。该协会实力雄厚，会员多达35 000人，挑战项目也不少，其中一项就是“十天四十八州骑行之旅”，又称为“48/10之旅”，也就是在10天时间内，环游美国本土的48个州。骑手可以选择任何路线，但是为了证明自己到过各州，必须拿到加油站收据之类的书面证据。2009年2月，一名女骑手Maura Gatensby发来一封电子邮件，想知道Dantzig-Fulkerson-Johnson的TSP路线都经过了哪些城市。

多数人研究这个问题的时候，都是拿到已有的地点和路线，然后想方设法削减路程。而对我来说，了解到数学中的这道题之后，我更愿意从Dantzig路线出发，当然也许会尝试移动某些地点来缩短距离，但是如果Dantzig路线并不算太长的话，我就干脆直接选定它，因为它具有重要的历史意义。有时候“最短的”路线未必就是“最好的”路线，因为追随大师的足迹更具有诗意和韵味。

如此将他们的最优解付诸实践，实在是恰到好处。

Gatensby女士在邮件中提到，迄今为止，“10天48州之旅”最短的路线是6967英里（11 212千米）。虽然对于今天的TSP求解程序来说，48个城市的情形并不难解决，但是这道题目还是很复杂，因为在各州都有很多城市可供选择。如果限定一些条件，比如各州目的地只限制在一系列已知的加油站范围内，那么寻找最优路线的挑战应该很有意思。

3.1.8 飞行时间

Ron Schreck的速度记录也许无人能敌。他住在北卡罗来纳州，驾驶RV-8飞机“Miss Izzy”四处飞行。2007年，他萌生了一个点子，决定在一整天内到达全州总共109家公共机场。Concorde程序为他提供了一条路线，他又稍作改动，使自己能在日出之前先到达几处设有跑道照明系统的机场。实际飞行的日子定在7月4日，因为那天是美国的公共假期，可以帮他避免延误起降时间。他当天的总飞行距离为1991英里（约3204公里），总时间为17个小时，平均每两次着陆之间只相隔9分半钟。这里所谓的“着陆”不是真正落地，基本上只是轮子接触地面一下，然后飞机立刻升回空中。

图3-3　驾驶Miss Izzy飞行途中（Ron Schreck供图）