9.1 计算模型

数学命题必须清晰准确才能有意义，至少必须能够改写成清晰准确的表述形式。百万美金的复杂性问题也不例外。我们必须明确所谓算法有什么意义，换言之，“可计算的”是什么意思。20世纪伊始，David Hilbert提出可判定性问题（Entscheidungsproblem），引起了人们对此的关注。可判定性问题大体相当于询问，是否存在一个算法，对任意给定命题都能判定它是否可以根据一组公理证明。解决此类问题的理论不断发展，成为20世纪数学的一项美妙成就，开路先锋是大师级人物Kurt Gödel（克尔特·哥德尔）、Alonzo Church（阿隆佐·邱奇）和Alan Turing（阿兰·图灵）。

算法的直观概念就是一系列合起来能够求解某问题的简单步骤。约在距今2300年前，欧几里得提供了计算最大公因数的算法。但直到Hilbert的年代，人们仍不清楚，如何才能给出算法的一般定义。在1936年那篇著名的论文中，图灵给出了一个答案，并引入了一类数学模型，称为图灵机（Turing machine）。¹

^{1.Turing, A. M. 1936. Proc. Lond. Math. Soc. 42, 230–265.}

图灵机有一条带子，用来存放符号；有一个读写头沿着带子移动，用来在各个存储单元里读取及写入符号；还有一个控制器，用来引导读写头移动。图灵机有一组数目有穷的状态，其中有两种特殊状态，分别是初始（initial）和停机（halt）。控制器实际上是一张表，指示处于特定状态s的机器在读入特定符号x时应该执行什么操作。具体说来，应该执行的操作有：在带单元内打印新符号x'，将读写头向左或向右移动一个单元，进入新状态s'。要想用图灵机解决问题，机器首先在初始状态启动，输入写在带子上，到达停机状态时便终止运行。

为了趣味性，可以考虑一台真实的图灵机，它的读写头沿着一条窄窄的长带子移动，带上写满了符号。事实上，有些学生改造了数个鞋盒，在每个鞋盒末端固定了一卷纸带，又在便笺本上记录下来状态之间的转移情况，把成品的照片传到了网上。图灵本人并没有提到真实的机器，而只是在论文中举了几个例子，强调说明了一个事实：写下一台机器的状态转移表，就可以完整地描述这台机器。

下面让我们考虑一个简单的例子：给定一串由0和1组成的数字串，试确定1的个数是奇数还是偶数。为了解决此问题，构造的图灵机可以有初始（initial）、奇数（odd）、偶数（even）、停机（halt）这四种状态，有0和1这两种符号，转移表如图9-1所示。表中，每行对应一个符号（包括空格“_”），每列对应停机以外的一种状态。每个表项都是三元序列，指明要写的符号，读写头在带上移动的方向，以及下一个状态。比如，机器如果处于奇数状态，并且读到符号1，那么就在单元内写入一个空格符号，向右移动一个单元，并改为偶数状态。如果给定由0和1组成的数字串，数字位于带子上的连续单元内，读写头位于最左端的符号处，那么我们的图灵机就会向右进行操作，直到遇到空单元才停止。空单元是串的结束标志。图灵机停机时，若1有偶数个，则在带上写入0；反之，若1有奇数个，则在带上写入1。过程简单明了，用转移表就说明了操作的概念。

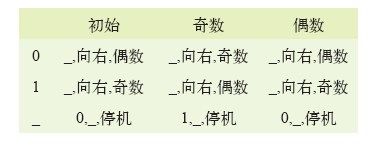
图9-1　奇偶性校验图灵机的转移表

下一步可以构建一台加法图灵机，对二进制表示的两个数求和。计算复杂性方面的大学课程中，这是一道常见的练习题，而且在这类题里面还算是挺有意思的。如果你想更加熟悉机器操作，我建议你也试试这道题。你会注意到，附加一条带子用来存储中间计算结果会很方便。所以，可以很自然地定义这一类图灵机，多带图灵机有多条带子，每条带都有单独的读写头。虽然附加带子能带来便利，但是不管想要计算什么，只要多带图灵机能做到，那么单带图灵机也一样能做到，只不过速度有点慢而已。

上面最后那句话的意思是说，单带图灵机可以模拟多带图灵机。这很重要。我们希望把算法定义成在单带图灵机上可执行的东西，不过这一条定义是否足以体现出我们对算法的一切要求呢？对此，只能回答：迄今为止，图灵机一直能够见招拆招，应付一切任务。某件事如果在现代计算机上是可计算的，那么迅如闪电的图灵机也能完成这一计算。

所以，我们可以把算法与图灵机等同看待，这种有效的假定称为邱奇-图灵论题（Church-Turing Thesis）。²该论题广受认可，它给出了算法的正式模型，使P与NP问题及其他复杂性问题得以准确表述。也许有朝一日，我们会遇到异乎寻常的计算能力，从而考虑对算法的定义进行扩充。不过，过去七十余年里，图灵提供的定义恰好足够满足研究界的需求。

^{2. 邱奇与图灵几乎同时完成研究。他用一种不同的框架结构描述了可计算性，后来图灵证明，这种描述和图灵机的概念实际是等价的。}

通用图灵机

举个例子，像iPhone这样的现代电话和我们脚上穿的鞋子之间有着根本性的区别。鞋子只是针对保护双脚的单一功能而设计的，但iPhone手机有数十万应用可供挑选，设计其硬件时想象不到的任务也能执行。我们把这当成是理所当然的事情，然而，发明可编程机器的这步飞跃却是充满智慧的创举，这正是图灵在那篇论文中提出的构想。

图灵机是用来描述算法意义的强大模型，但是一种图灵机只是为了一个任务而设计的，比如对两个数求和。按照这种意义理解，图灵机更像是鞋子而不是iPhone。不过图灵指出了至关重要的一点：可以设计通用图灵机（Universal Turing machine），它能够模拟每一种图灵机。

可以发明一台机器，它能用来计算任何可计算序列。如果向这台机器U提供一条带子，带子起始端写有某种计算机器M的S.D.，那么U就能像M一样计算同一段序列。

这段引文中的“S.D.”是“标准描述”（standard description）的缩写，图灵用这一术语来称呼转移表。因此，上文的意思是说，要在带输入中包含一个转移表，就像在现代计算机中包含一个程序一样。图灵的想法，再加上Konrad Zuse和约翰·冯·诺依曼等人的辛勤工作，共同开启了计算时代。