1.2 中国象棋将帅问题
下过中国象棋的朋友都知道,双方的“将”和“帅”相隔遥远,并且它们不能照面。在象棋残局中,许多高手能利用这一规则走出精妙的杀招。假设棋盘上只有“将”和“帅”二子(如图1-3所示)(为了下面叙述方便,我们约定用A表示“将”,B表示“帅”):
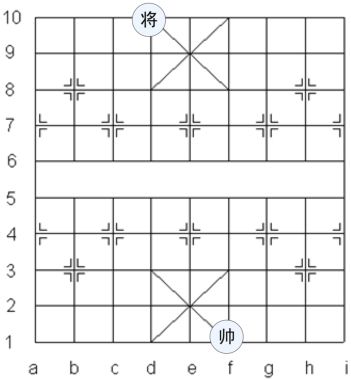
图1-3
A、B二子被限制在己方3×3的格子里运动。例如,在如上的表格里,A被正方形{d10,f10,d8,f8}包围,而B被正方形{d3,f3,d1,f1}包围。每一步,A、B分别可以横向或纵向移动一格,但不能沿对角线移动。另外,A不能面对B,也就是说,A和B不能处于同一纵向直线上(比如A在d10的位置,那么B就不能在d1、d2以及d3)。
请写出一个程序,输出A、B所有合法位置。要求在代码中只能使用一个变量。
分析与解法
问题的本身并不复杂,只要把所有A、B互相排斥的条件列举出来就可以完成本题的要求。由于本题要求只能使用一个变量,所以必须首先想清楚在写代码的时候,有哪些信息需要存储,并且尽量高效率地存储信息。稍微思考一下,可以知道这个程序的大体框架是:

因此,需要存储的是A、B的位置信息,并且每次循环都要更新。为了能够进行判断,首先需要创建一个逻辑的坐标系统,以便检测A何时会面对B。这里我们想到的方法是用1~9的数字,按照行优先的顺序来表示每个格点的位置(如图1-4所示)。这样,只需要用模余运算就可以得到当前的列号,从而判断A、B是否互斥。
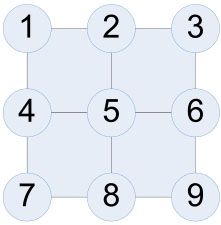
图1-4 用1~9的数字表示A、B的坐标
第二,题目要求只用一个变量,但是我们却要存储A和B两个子的位置信息,该怎么办呢?
可以先把已知变量类型列举一下,然后做些分析。
对于bool类型,估计没有办法做任何扩展了,因为它只能表示true和false两个值;而byte或者int类型,它们能够表达的信息则更多。事实上,对本题来说,每个子都只需要9个数字就可以表达它的全部位置。
一个8位的byte类型能够表达28=256个值,所以用它来表示A、B的位置信息绰绰有余,因此可以把这个字节的变量(设为b)分成两部分。用前面的4bit表示A的位置,用后面的4bit表示B的位置,那么4个bit可以表示16个数,这已经足够了。
问题在于:如何使用bit级的运算将数据从这一byte变量的左边和右边分别存入和读出。
下面是做法:
■ 将byte b(10100101)的右边4bit(0101)设为n(0011):
首先清除b右边的bits,同时保持左边的bits:

然后将上一步得到的结果与n做或运算

■ 将byte b(10100101)左边的4bit(1010)设为n(0011):
首先,清除b左边的bits,同时保持右边的bits:

现在,把n移动到byte数据的左边
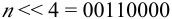
然后对以上两步得到的结果做或运算,从而得到最终结果。

■ 得到byte数据的右边4bits或左边4bits(e.g.10100101中的1010以及0101):
清除b左边的bits,同时保持右边的bits

清除b的右边的bits,同时保持左边的bits

将结果右移4bits
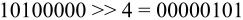
最后的挑战是如何在不声明其他变量约束的前提下创建一个for循环。可以重复利用1byte的存储单元,把它作为循环计数器并用前面提到的存取和读入技术进行操作。还可以用宏来抽象化代码,例如:

【解法一】
代码清单1-6

【输出】
格子的位置用N来表示,N=1,2,…,8,9,依照行优先的顺序,如图1-5所示:
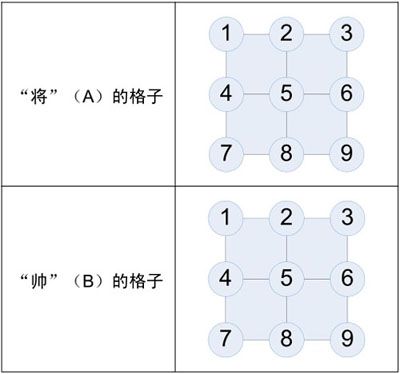
图1-5
| A=1,B=2 | A=4,B=2 | A=7,B=2 |
| A=1,B=3 | A=4,B=3 | A=7,B=3 |
| A=1,B=5 | A=4,B=5 | A=7,B=5 |
| A=1,B=6 | A=4,B=6 | A=7,B=6 |
| A=1,B=8 | A=4,B=8 | A=7,B=8 |
| A=1,B=9 | A=4,B=9 | A=7,B=9 |
| A=2,B=1 | A=5,B=1 | A=8,B=1 |
| A=2,B=3 | A=5,B=3 | A=8,B=3 |
| A=2,B=4 | A=5,B=4 | A=8,B=4 |
| A=2,B=6 | A=5,B=6 | A=8,B=6 |
| A=2,B=7 | A=5,B=7 | A=8,B=7 |
| A=2,B=9 | A=5,B=9 | A=8,B=9 |
| A=3,B=1 | A=6,B=1 | A=9,B=1 |
| A=3,B=2 | A=6,B=2 | A=9,B=2 |
| A=3,B=4 | A=6,B=4 | A=9,B=4 |
| A=3,B=5 | A=6,B=5 | A=9,B=5 |
| A=3,B=7 | A=6,B=7 | A=9,B=7 |
| A=3,B=8 | A=6,B=8 | A=9,B=8 |
考虑了这么多因素,总算得到了本题的一个解法,但是MSRA里却有人说,下面的一小段代码也能达到同样的目的:

但是很快又有另一个人说他的解法才是效率最高的:
代码清单1-7

读者能自己证明一下么?⑤
