4.4　点是否在三角形内

如果在一个二维坐标系中，已知三角形三个点的坐标，那么对于坐标系中的任意一点，如何判断该点是否在三角形内（点在三角形边线上也认为在三角形内）？

假设三角形的三个点的坐标为ABC（逆时针顺序），需要判断点D是否在该三角形内。

这个问题比较简单，但是可以通过多种有趣的思路来避免采用复杂的计算方式。

分析与解法

当你开始解答此题时，很可能会直接研究这个任意点与三角形的三个顶点或三条边之间的关系，进而做出判断。在试着摆放时，你可能会发现，利用垂线的交点可以进行分析（如图4-4所示）：

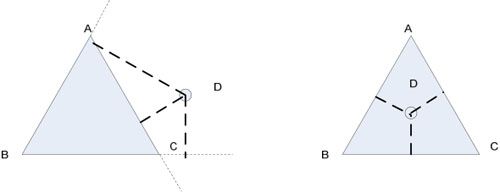
图4-4　利用垂线信息判断点与三角形的关系

从图4-4中可以直观地分析出，如果点D在三角形内，则所有的垂线交点都在三角形的边线之内。而如果点D在三角形之外，则垂线的交点就会在三角形边线的延长线上。

但图4-4的情况是否具有通用性呢？且慢！我们再考虑其他情况看看。如图4-5所示，如果D点很靠近三角形，或者此三角形是钝角三角形，那我们上面的“直观分析”都是不对的，看来我们的第一次尝试并不可取。

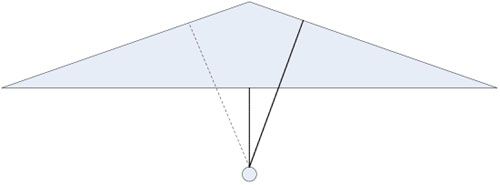
图4-5　垂足全部在三角形以内的情况

【解法一】

我们再研究点和线段之间的关系，可以考虑把点D和其他的三个点连接起来进行分析。也就是利用图4-6的图形来分析这个问题：

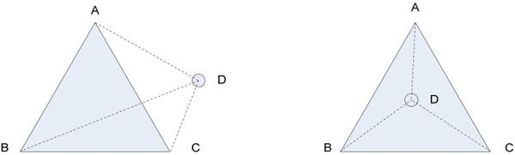
图4-6　利用面积来判断点与三角形的关系

从图中可以看出，这个问题可以非常直观地转化为比较三角形的面积来判断点的位置，即通过比较三角形ABC的面积与三角形ABD、BCD、CAD面积之和的大小来判断点是否在三角形内。

设S＝Area（ABC）、S₁＝Area（ABD）、S₂＝Area（BCD）、S₃＝Area（CAD）。

如果S＝S₁＋S₂＋S₃，那么点D在三角形ABC的内部或边上；如果S₁＋S₂＋S₃＞S，则点D在三角形外部。

按照这种算法，计算量会大大减少。

代码清单4-1

注：此处利用了浮点计算来判断if（Area（A，B，D）＋Area（B，C，D）＋Area（C，A，D）＞Area（A，B，C）），由于浮点有精度问题，有可能计算有误差。但是，这不是本题的重点，它不会影响读者理解逻辑。

【解法二】

仍然考虑从点和直线之间的关系着手，从下面的图4-7中，我们可发现如下的规律：

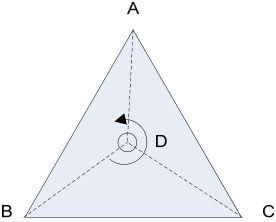
图4-7　利用点与直线的关系

由于三角形是凸的，所以如果有一个点D在三角形ABC内，那么沿着三角形的边界逆时针走，点D一定保持在边界的左边，也就是说点D在边AB、BC、CA的左边。

判断一个点P₃是否在一条射线P₁P₂的左边，可以通过P₁P₂，P₁P₃两个向量叉积的正负来判断。如图4-8所示：

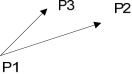
图4-8　点关系的矢量表示

如果叉积为正，则P₃在射线P₁P₂的左边；如果叉积为负，则P₃在射线P₁P₂的右边；如果叉积为0，则P₃在射线P₁P₂上。

代码清单4-2

扩展问题

如果不包括点在边线上的情形，这些解法需要做什么修改？

若要判断一个点是否在一个凸多边形内呢？

进一步，如何判断一个点是否在一个不自交多边形（不保证为凸的）内？

或者又怎么判断一个点是否在一个四面体内呢？