4.7　蚂蚁爬杆

有一根27厘米的细木杆，在第3厘米、7厘米、11厘米、17厘米、23厘米这五个位置上各有一只蚂蚁。木杆很细，不能同时通过两只蚂蚁。开始时，蚂蚁的头朝左还是朝右是任意的，它们只会朝前走或调头，但不会后退。当任意两只蚂蚁碰头时，两只蚂蚁会同时调头朝反方向走。假设蚂蚁们每秒钟可以走一厘米的距离。编写程序，求所有蚂蚁都离开木杆的最短时间和最长时间。

分析与解法

【解法一】

面试中有些问题，其表面上的复杂性，会导致应聘者使用蛮力（brute force）的方法来解决。对于这道题，应聘者可能会考虑枚举蚂蚁的初始朝向，模拟每一个蚂蚁的运动来解决。显然，程序将既缺乏可读性，又缺乏灵活性和效率，显然不足以打动面试者。

【解法二】

其实每个复杂问题的背后，都有一些简单的规律，无论是在面试中还是在实际工作中都是这样。而这种化繁为简的能力正是面试者所期望的。问题是求所有蚂蚁离开木杆的时间，并不需要具体蚂蚁的运动信息，因此就有了利用简便方法的机会。

首先对蚂蚁的运动情况进行分析。当两个蚂蚁碰头的时候，会发生怎样的情况？

图4-11是两只蚂蚁碰头过程的示意图，从上到下分别为碰头前、碰头、碰头后。

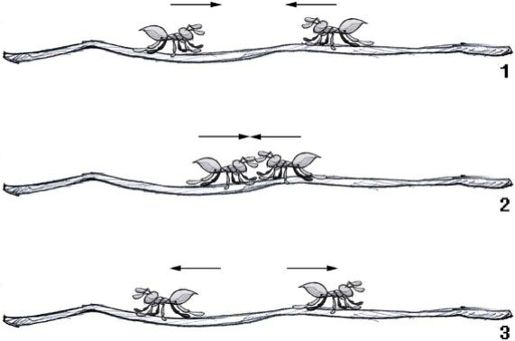
图4-11　蚂蚁爬杆示意图

从图4-11中可以分析出，虽然两个蚂蚁相遇后是掉头往反向走，但是，可以“看作”是两个蚂蚁相遇后，擦肩而过。也就是说，可以认为蚂蚁的运动是独立的，是否有碰头并不是问题的重点。

这样，虽然每个蚂蚁运动的轨迹都与原来不一样了，但所有蚂蚁离开木杆的最短时间和最长时间是不变的。只需分别计算每个蚂蚁离开木杆的时间，即可求出所有蚂蚁离开木杆的时间了。

这样，程序只需遍历所有蚂蚁，把每个蚂蚁走出木杆的最长时间（蚂蚁向离自己较远的一端走去），最短时间（蚂蚁向离自己较近的一端走去）分别求出来，得到最大值，就是所有蚂蚁离开木杆的最短时间和最长时间。

伪代码如下：

代码清单4-3

扩展问题

1．第i个蚂蚁，什么时候走出木杆？

2．如果蚂蚁在一个平面上运动，同样也是碰头后原路返回（这样和弹性碰撞不同，没有相当于两个蚂蚁交换继续前进的本质），问蚂蚁如何走出平面？

3．问蚂蚁一共会碰撞多少次？

4．两人A（速度为a），B（速度为b）在一直路上相向而行。在A、B距离s的时候，A放出一只鸽子C（速度为c），C飞到B后，立即调头飞向A，遇到A后又飞向B……就这样在AB间飞来飞去，直到AB相遇。问这期间鸽子共飞了多少路程？

5．轮船（速度为a）在长江（速度为b）里逆流而上行驶。某个时刻，从船上落下一个救生圈到水中。一个小时后，船员才发现这一情况，于是调头去找。问什么时候轮船可找到这个救生圈？