2.7　最大公约数问题

写一个程序，求两个正整数的最大公约数。如果两个正整数都很大，有什么简单的算法吗？

分析与解法

求最大公约数是一个很基本的问题。早在公元前300年左右，欧几里得就在他的著作《几何原本》中给出了高效的解法——辗转相除法。辗转相除法使用到的原理很聪明也很简单，假设用f（x，y）表示x，y的最大公约数，取k＝x/y，b＝x％y，则x＝ky＋b，如果一个数能够同时整除x和y，则必能同时整除b和y；而能够同时整除b和y的数也必能同时整除x和y，即x和y的公约数与b和y的公约数是相同的，其最大公约数也是相同的，则有f（x，y）＝f（y，y％x）（y＞0），如此便可把原问题转化为求两个更小数的最大公约数，直到其中一个数为0，剩下的另外一个数就是两者最大的公约数。辗转相除法更详细的证明可以在很多的初等数论相关书籍中找到，或者读者也可以试着证明一下。

示例如下：

f（42，30）＝f（30，12）＝f（12，6）＝f（6，0）＝6

【解法一】

最简单的实现，就是直接用代码来实现辗转相除法。从上面的描述中，我们知道，利用递归就能够很轻松地把这个问题完成。

具体代码如下：

【解法二】

在解法一中，我们用到了取模运算。但对于大整数而言，取模运算（其中用到除法）是非常昂贵的开销，将成为整个算法的瓶颈。有没有办法能够不用取模运算呢？

采用类似前面辗转相除法的分析，如果一个数能够同时整除x和y，则必能同时整除x－y和y；而能够同时整x－y和y的数也必能同时整除x和y，即x和y的公约数与x－y和y的公约数是相同的，其最大公约数也是相同的，即f（x，y）＝f（x－y，y），那么就可以不再需要进行大整数的取模运算，而转换成简单得多的大整数的减法。

在实际操作中，如果x＜y，可以先交换（x，y）（因为（x，y）＝（y，x）），从而避免求一个正数和一个负数的最大公约数情况的出现。一直迭代下去，直到其中一个数为0。

示例如下：

f（42，30）＝f（30，12）＝f（12，18）＝f（18，12）＝f（12，6）＝f（6，6）＝f（6，0）＝6

解法二的具体代码如下：

代码清单2-15

代码中BigInt是读者自己实现的一个大整数类（所谓大整数当然可以是成百上千位），那么就要求读者重载该大整数类中的减法运算符“－”，关于大整数的具体实现这里不再赘述，若读者只是想验证该算法的正确性，完全可使用系统内建的int型来测试。

这个算法，免去了大整数除法的繁琐，但是同样也有不足之处。最大的瓶颈就是迭代的次数比之前的算法多了不少，如果遇到（10000000000000，1）这类情况，就会相当地令人郁闷了。

【解法三】

解法一的问题在于计算复杂的大整数除法运算，而解法二虽然将大整数的除法运算转换成了减法运算，降低了计算的复杂度，但它的问题在于减法的迭代次数太多，那么能否结合解法一和解法二从而使其成为一个最佳的算法呢？答案是肯定的。

首先从分析公约数的特点入手：

对于y和x来说，如果y＝ky₁，x=kx₁。那么有f（y，x）＝k*f（y₁，x₁）。

另外，如果x＝px₁，假设p是素数，并且y％p！＝0（即y不能被p整除），那么f（x，y）＝f（px₁，y）＝f（x₁，y）。

注意到以上两点之后，我们就可以利用这两点对算法进行改进。

最简单的方法是，我们知道，2是一个素数，同时对于二进制表示的大整数而言，可以很容易地将除以2和乘以2的运算转换成移位运算，从而避免大整数除法，由此就可以利用2这个数字来进行分析。

取p＝2

若x，y均为偶数，f（x，y）＝2f（x/2，y/2）＝2f（x＞＞1，y＞＞1）

若x为偶数，y为奇数，f（x，y）＝f（x/2，y）＝f（x＞＞1，y）

若x为奇数，y为偶数，f（x，y）＝f（x，y/2）＝f（x，y＞＞1）

若x，y均为奇数，f（x，y）＝f（x，x－y），

那么在f（x，y）＝f（x，x－y）之后，（x－y）是一个偶数，下一步一定会有除以2的操作。

因此，最坏情况下的时间复杂度是O（log₂（max（x，y））。

考虑如下的情况：

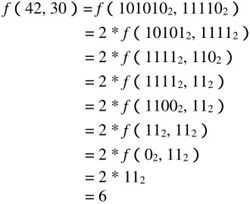
根据上面的规律，具体代码实现如下：

代码清单2-16

BigInt见解法二中的解释，IsEven（BigInt x）函数检查x是否为偶数，如果x为偶数，则返回true，否则返回false。

解法三很巧妙地利用移位运算和减法运算，避开了大整数除法，提高了算法的效率。程序员常常将移位运算作为一种技巧来使用，最常见的就是通过左移或右移来实现乘以2或除以2的操作。其实移位的用处远不止于此，如求一个整数的二进制表示中1的个数问题（见本书2.1节“求二进制数中1的个数”）和逆转一个整数的二进制表示问题等，往往让人拍案叫绝。