2.15　子数组之和的最大值（二维）

我们在前面分析了一维数组的子数组之和最大值的问题，那么如果是二维数组又该如何分析呢？

分析与解法

最直接的方法，当然就是枚举每一个矩形区域，然后再求这个矩形区域中元素的和。

【解法一】

代码清单2-29

采用这种方法的时间复杂度为O（N²M²Sum的时间复杂度）。上面Sum函数是以（i_min，j_min）、（i_min，j_max）、（i_max，j_min）、（i_max，j_max）为顶点的矩形区域（图2-14的灰色部分）中元素之和。求矩形区域中元素之和若仍采用最直接的遍历，时间复杂度就太大了。

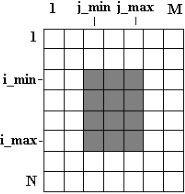
图2-14　二维最大值示意图

考虑到区域的和需要被频繁计算，或许我们可以做一些预处理，并把计算结果存下来，以达到“空间换时间”的目的。事实上，的确可以这样做。通过“部分和”的O（N*M）预处理，可以在O（1）时间内计算出任意一个区域的和。

关于“部分和”，先看一维数组（A[1]，…，A[n]），如果事先记录下PS[i]：

PS[0]＝0，边界值

PS[i]＝PS[i－1]＋A[i]＝A[1]＋…＋A[i]（0＜i＜＝n）

那么，数组中任意一段（A[i]，…，A[j]）的元素之和等于PS[j]－PS[i－1]。

类似地，在二维情况下，定义“部分和”PS[i][j]等于以（1，1），（i，1），（1，j），（i，j）为顶点的矩形区域的元素之和。

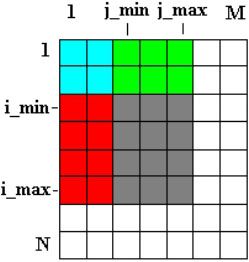
图2－15　二维最大值示意图

通过图2－15也可以看出，以（i_min，j_min），（i_min，j_max），（i_max，j_min），（i_max，j_max）为顶点的矩形区域的元素之和，等于PS[i_max][j_max]－PS[i_min－1][j_max]－PS[i_max][j_min－1]＋PS[i_min－1][j_min－1]。也就是在已知“部分和”的基础上可以用O（1）时间算出任意矩形区域的元素之和。

万事俱备，只欠“部分和”。怎么快速预处理以得到所有“部分和”呢？

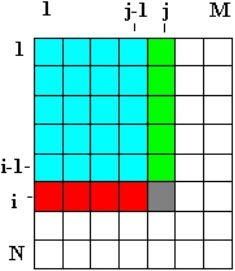
图2-16　二维最大值示意图

观察图2-16不难看出，在更小“部分和”的基础上，也能以O（1）时间得到新的“部分和”。图2-16中PS[i][j]＝PS[i－1][j]＋PS[i][j－1]－PS[i－1][j－1]＋B[i][j]，其中B[i][j]为矩阵中第i行第j列的元素（下标从1开始）。因此，O（N*M）的时间就足够预处理并得到所有部分和：

综上所述，我们得到了一个时间复杂度为O（N²*M²）的解法。

【解法二】

是否还可以找到更快的方法呢？前面我们发现一维的解答可以线性完成。如果我们能把问题从二维转化为一维，或许可以再改进一下。

假设已经确定了矩形区域的上下边界，比如知道矩形区域的上下边界分别是第a行和第c行，现在要确定左右边界。

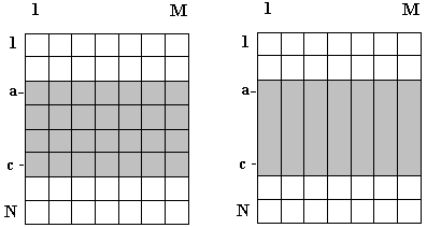
图2-17　二维示意图

如图2-17所示，其实这个问题就是一维的，可以把每一列中第a行和第c行之间的元素看成一个整体。即求数组（BC[1]，…，BC[M]）中和最大的一段，其中BC[i]＝B[a][i]＋…＋B[c][i]。

这样，我们枚举矩形上下边界，然后再用一维情况下的方法确定左右边界，就可以得到二维问题的解。新方法的时间复杂度为O（N²*M）。

代码清单2-30

BC（a，c，i），表示在第a行和第c行之间的第i列的所有元素的和，显然可以通过“部分和”在O（1）时间内计算出来，它等于PS[c][i]－PS[a－1][i]－PS[c][i－1]＋PS[a－1][i－1]。

当然，也可以枚举左右边界，再用一维情况下的方法确定上下边界，它们本质上是一样的。至此，这个问题只需O（NMmin（N，M））的时间就可以解决了。

扩展问题

1．如果二维数组也是首尾相连，像一条首尾相连的带子，算法会如何改变？

图2-18

2．在上面的基础上，如果这个二维数组的上下也相连，就像一个游泳圈（如图2-18所示），算法应该怎样修改？

3．在三维数组C[i][j][k]（1＜＝i＜＝N，1＜＝j＜＝M，1＜＝k＜＝L）中找出一块长方体，使得和最大。

4．如果再将问题扩展到四维的情况又如何呢？请读者根据以上的分析，想出一个优化解法。

还有一个扩展问题……算了，下次吧。☺