2.11　寻找最近点对

给定平面上N个点的坐标，找出距离最近的两个点（如图2-8所示）。

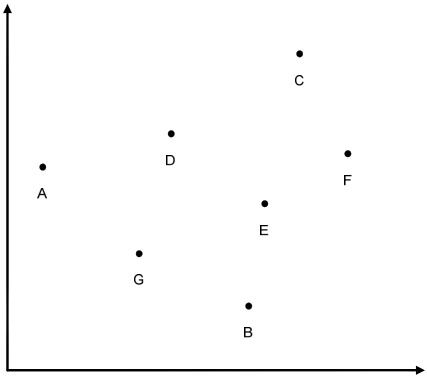
图2-8　七个平面上的点

分析与解法

初看这个问题，会觉得不太容易解答，没有什么头绪，在面试的时候，怎么办？我们不妨先看看一维的情况：在一个包含N个数的数组中，如何快速找出N个数中两两差值的最小值？一维的情况相当于所有的点都在一条直线上。虽然是一个退化的情况，但还是能从中得到一些启发。

【解法一】

数组中总共包含N个数，我们把它们两两之间的差值都求出来，那样就不难得出最小的差值了。这样一个直接的想法，时间复杂度为O（N²）。伪代码如下：

代码清单2-21

如果扩展到二维的情况，那就相当于枚举任意两个点，然后再记录下距离最近的点对。时间复杂度也是O（N²）。这还是一个很直接的想法，能否继续改进呢？

【解法二】

如果数组有序，找出最小的差值就很容易了。可以用O（Nlog₂N）的算法进行排序（快速排序、堆排序、归并排序等）。排序完成后，找最小差值只需要O（N）的时间，总时间复杂度是O（Nlog₂N）。

代码清单2-22

在一维情况下，时间复杂度改进了不少。但是这个方法不能推广到二维的情况，因为距离最近的点对不能保证是映射到某条直线之后紧靠着的两个点。如图2-9所示，点A和C的距离最近，但它们在X轴上的投影点却不是相邻的。

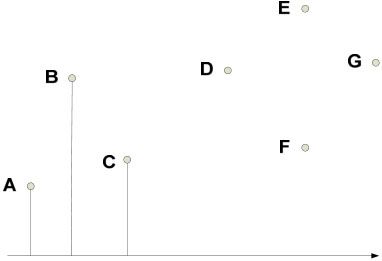
图2-9　二维投影示意图

【解法三】

还有什么想法呢？如果我们用数组的中间值k把数组分成Left、Right两部分，小于k的数为Left部分，其他的为Right部分，那么这个最小差值要么来自Left部分，要么来自Right部分，要么是Left中最大数和Right中最小数的差值。在这里，我们其实借用了分治思想。时间复杂度仍然为O（N*log₂N）。

这个方法中的分治思想也可以扩展到二维的情况：

根据水平方向的坐标把平面上的N个点分成两部分Left和Right。跟以往一样，我们希望这两个部分点数的个数差不多。假设分别求出了Left和Right两个部分中距离最近的点对之最短距离为MinDist（Left）和MinDist（Right），还有一种情况我们没有考虑，那就是点对中一个点来自于Left部分，另一个点来自于Right部分。最直接的想法，那就是穷举Left和Right两个部分之间的点对，这样的点对很多，最多可能有N*N/4对。显然，穷举所有Left和Right之间的点对是不好的做法。是否可以只考虑有可能成为最近点对的候选点对呢？由于我们已经知道Left和Right两个部分中的最近点对距离分别为MinDist（Left）和MinDist（Right），如果Left和Right之间的点对距离超过MDist＝MinValue（MinDist（Left），MinDist（Right）），我们则对它们并不感兴趣，因为这些点对不可能是最近点对。

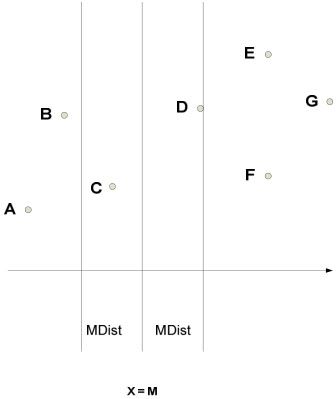
图2-10　二维点分布示意图

如图2-10所示，通过直线x＝M将所有的点分成x＜M和x＞M两部分，在分别求出两部分的最近点对之后，只需要考虑点对CD。因为其他点对AD、BD、CE、CF、CG等都不可能成为最近点对。也就是说，只要考虑从x＝M－Mdist到x＝M＋MDist之间这个带状区域内的最小点对，然后再跟MDist比较就可以了。在计算带状区域的最小点对时，可以按Y坐标，对带状区域内的顶点进行排序。如果一个点对的距离小于MDist，那么它们一定在一个MDist（2Mdist）的区域内（如图2-11所示）：

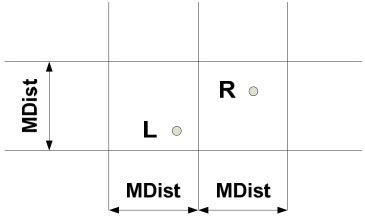
图2-11　区域示意图

而在左右两个Mdist*MDist正方形区域内，最多都只能含有4个点。如果超过4个点，则这个正方形区域内至少存在一个点对的距离小于Mdist，这跟x＜M和x＞M两个部分的最近点对距离分别是MinDist（Left）和MinDist（Right）矛盾。

图2-12　区域示意图

因此，一个MDist（2Mdist）的区域内最多有8个点（如图2-12所示）。对于任意一个带状区域内的顶点，只要考察它与按Y坐标排序且紧接着的7个点之间的距离就可以了。根据这个特点，我们可用O（N）时间完成带状区域最近点对的查找。在这一步，需要注意的是：我们可以用归并排序法将带状区域的点按Y坐标排序。归并排序的过程与计算最近点对的算法结合在一起。

整个算法的时间复杂度f（N）的递归表达式为：

F（2）＝1

F（3）＝3

F（N）＝2*f（N/2）＋O（N）（N＞2）

可以计算出f（N）＝Nlog₂N。也就是说，我们用O（Nlog₂N）的时间可以完成最近点对问题。

扩展问题

1．如果给定一个数组arr[0，…，N－1]，要求找出相邻两个数的最大差值。对于数X和Y，如果不存在其他数组中的数在[X，Y]区间内，则我们称X和Y是相邻的。

我们也可以使用上面的方法来解决这个扩展问题。不过，这个扩展问题还有一个更漂亮的解法。如果在这个数组arr中，最大的数为arr.MaxValue，而最小的数为arr.MinValue，那么根据抽屉原理，相邻两个数的最大差值一定不小于delta＝（arr.MaxValue－arr.MinValue）/（N－1）。

证明：假设任意相邻两个数的差值都小于delta，而数组arr从小到大排好序后得到数组sorted_arr，sorted_arr[0]＜sorted_arr[1]＜…＜sorted_arr[N－1]，则sorted_arr[1]－sorted_arr[0]＜delta，sorted_arr[2]－sorted_arr[1]＜delta，…，sorted_arr[N－1]－sorted_arr[N－2]＜delta，有arr.MaxValue－arr.MinValue＝sorted_arr[N－1]－sorted_arr[0]＝（sorted_arr[N－1]－sorted_arr[N－2]）＋…＋（sorted_arr[1]－sorted_arr[0]）＜delta*（N－1）＝arr.MaxValue－arr.MinValue。那么它与假设矛盾。

通过上面的分析，我们知道最大的差值大于等于delta。因此，我们忽略小于delta的差值，因为这些差值都不可能是答案。一个方法就是我们把区间[arr.MinValue，arr.MaxValue]分成N个桶：[arr.MinValue，arr.MinValue]，[arr.MinValue＋delta]，[arr.MinValue＋delta，arr.MinValue＋delta*2]，…，[arr.MaxValue－delta，arr.MaxValue]。综合上面的分析，我们知道最大的差值应该出现在不同的桶之间（除非delta＝0），因为处于同一个桶的两个数的差值不超过delta，我们可以忽略不计。既然最大的差值处于两个不同的桶之间，那么它们就等于某个桶的最小值与前一个非空桶的最大值的差值。

根据上面的分析，可以申请O（N）大小的空间来存储每一个桶的最大值和最小值，然后再扫描一遍所有的桶就可以得到整个数组的最大差值。整个算法的空间复杂度和时间复杂度均为O（N）。

2．如果给定的是平面上的N个点，如何寻找距离最远的两个点呢？