2.5　寻找最大的K个数

在面试中，有下面的问答：

问：有很多个无序的数，我们姑且假定它们各不相等，怎么选出其中最大的若干个数呢？

答：可以这样写：int array[100]……

问：好，如果有更多的元素呢？

答：那可以改为：int array[1000]……

问：如果我们有很多元素，例如1亿个浮点数，怎么办？

答：个，十，百，千，万……那可以写：float array[100000000]……

问：这样的程序能编译运行么？

答：嗯……我从来没写过这么多的0……

分析与解法

【解法一】

当学生们信笔写下float array[10000000]，他们往往没有想到这个数据结构要如何在电脑上实现，是从当前程序的栈（Stack）中分配，还是堆（Heap），还是电脑的内存也许放不下这么大的东西？

我们先假设元素的数量不大，例如在几千个左右，在这种情况下，那我们就排序一下吧。在这里，快速排序或堆排序都是不错的选择，他们的平均时间复杂度都是O（Nlog₂N）。然后取出前K个，O（K）。总时间复杂度O（Nlog₂N）＋O（K）＝O（N*log₂N）。

你一定注意到了，当K＝1时，上面的算法也是O（N*log₂N）的复杂度，而显然我们可以通过N－1次的比较和交换得到结果。上面的算法把整个数组都进行了排序，而原题目只要求最大的K个数，并不需要前K个数有序，也不需要后N－K个数有序。

怎么能够避免做后N－K个数的排序呢？我们需要部分排序的算法，选择排序和交换排序都是不错的选择。把N个数中的前K大个数排序出来，复杂度是O（N*K）。

那一个更好呢？O（Nlog₂N）还是O（NK）？这取决于K的大小，这是你需要在面试者那里弄清楚的问题。在K（K＜＝log₂N）较小的情况下，可以选择部分排序。

在下一个解法中，我们会通过避免对前K个数排序来得到更好的性能。

【解法二】

回忆一下快速排序，快排中的每一步，都是将待排数据分做两组，其中一组的数据的任何一个数都比另一组中的任何一个大，然后再对两组分别做类似的操作，然后继续下去……

在本问题中，假设N个数存储在数组S中，我们从数组S中随机找出一个元素X，把数组分为两部分S_a和S_b。S_a中的元素大于等于X，S_b中元素小于X。

这时，有两种可能性：

1．S_a中元素的个数小于K，S_a中所有的数和S_b中最大的K－|S_a|个元素（|S_a|指S_a中元素的个数）就是数组S中最大的K个数。

2．S_a中元素的个数大于或等于K，则需要返回S_a中最大的K个元素。

这样递归下去，不断把问题分解成更小的问题，平均时间复杂度O（N*log₂K）。伪代码如下：

代码清单2-11

【解法三】

寻找N个数中最大的K个数，本质上就是寻找最大的K个数中最小的那个，也就是第K大的数。可以使用二分搜索的策略来寻找N个数中的第K大的数。对于一个给定的数p，可以在O（N）的时间复杂度内找出所有不小于p的数。假如N个数中最大的数为V_max，最小的数为V_min，那么这N个数中的第K大数一定在区间[V_min，V_max]之间。那么，可以在这个区间内二分搜索N个数中的第K大数p。伪代码如下：

代码清单2-12

伪代码中f（arr，N，V_mid）返回数组arr[0，…，N－1]中大于等于V_mid的数的个数。

上述伪代码中，delta的取值要比所有N个数中的任意两个不相等的元素差值之最小值小。如果所有元素都是整数，delta可以取值0.5。循环运行之后，得到一个区间（V_min，V_max），这个区间仅包含一个元素（或者多个相等的元素）。这个元素就是第K大的元素。整个算法的时间复杂度为O（Nlog₂（|V_max－V_min|/delta））。由于delta的取值要比所有N个数中的任意两个不相等的元素差值之最小值小，因此时间复杂度跟数据分布相关。在数据分布平均的情况下，时间复杂度为O（Nlog₂（N））。

在整数的情况下，可以从另一个角度来看这个算法。假设所有整数的大小都在[0，2^m－1]之间，也就是说所有整数在二进制中都可以用m bit来表示（从低位到高位，分别用0，1，…，m－1标记）。我们可以先考察在二进制位的第（m－1）位，将N个整数按该位为1或者0分成两个部分。也就是将整数分成取值为[0，2^m－1－1]和[2^m－1，2^m－1]两个区间。前一个区间中的整数第（m－1）位为0，后一个区间中的整数第（m－1）位为1。如果该位为1的整数个数A大于等于K，那么，在所有该位为1的整数中继续寻找最大的K个。否则，在该位为0的整数中寻找最大的K－A个。接着考虑二进制位第（m－2）位，以此类推。思路跟上面的浮点数的情况本质上一样。

对于上面两个方法，我们都需要遍历一遍整个集合，统计在该集合中大于等于某一个数的整数有多少个。不需要做随机访问操作，如果全部数据不能载入内存，可以每次都遍历一遍文件。经过统计，更新解所在的区间之后，再遍历一次文件，把在新的区间中的元素存入新的文件。下一次操作的时候，不再需要遍历全部的元素。每次需要两次文件遍历，最坏情况下，总共需要遍历文件的次数为2*log₂（|V_max－V_min|/delta）。由于每次更新解所在区间之后，元素数目会减少。当所有元素能够全部载入内存之后，就可以不再通过读写文件的方式来操作了。

此外，寻找N个数中的第K大数，是一个经典问题。理论上，这个问题存在线性算法。不过这个线性算法的常数项比较大，在实际应用中效果有时并不好。

【解法四】

我们已经得到了三个解法，不过这三个解法有个共同的地方，就是需要对数据访问多次，那么就有下一个问题，如果N很大呢，100亿？（更多的情况下，是面试者问你这个问题）。这个时候数据不能全部装入内存（不过也很难说，说知道以后会不会1T内存比1斤白菜还便宜），所以要求尽可能少的遍历所有数据。

不妨设N＞K，前K个数中的最大K个数是一个退化的情况，所有K个数就是最大的K个数。如果考虑第K＋1个数X呢？如果X比最大的K个数中的最小的数Y小，那么最大的K个数还是保持不变。如果X比Y大，那么最大的K个数应该去掉Y，而包含X。如果用一个数组来存储最大的K个数，每新加入一个数X，就扫描一遍数组，得到数组中最小的数Y。用X替代Y，或者保持原数组不变。这样的方法，所耗费的时间为O（N*K）。

进一步，可以用容量为K的最小堆来存储最大的K个数。最小堆的堆顶元素就是最大K个数中最小的一个。每次新考虑一个数X，如果X比堆顶的元素Y小，则不需要改变原来的堆，因为这个元素比最大的K个数小。如果X比堆顶元素大，那么用X替换堆顶的元素Y。在X替换堆顶元素Y之后，X可能破坏最小堆的结构（每个结点都比它的父亲结点大），需要更新堆来维持堆的性质。更新过程花费的时间复杂度为O（log₂K）。

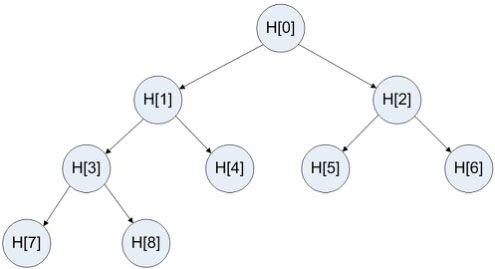
图2-1

图2-1是一个堆，用一个数组h[]表示。每个元素h[i]，它的父亲结点是h[i/2]，儿子结点是h[2i＋1]和h[2i＋2]。每新考虑一个数X，需要进行的更新操作伪代码如下：

代码清单2-13

因此，算法只需要扫描所有的数据一次，时间复杂度为O（Nlog₂K）。这实际上是部分执行了堆排序的算法。在空间方面，由于这个算法只扫描所有的数据一次，因此我们只需要存储一个容量为K的堆。大多数情况下，堆可以全部载入内存。如果K仍然很大，我们可以尝试先找最大的K＇个元素，然后找第K＇＋1个到第2K＇个元素，如此类推（其中容量K＇的堆可以完全载入内存）。不过这样，我们需要扫描所有数据ceil^②（K/K＇）次。

【解法五】

上面类快速排序的方法平均时间复杂度是线性的。能否有确定的线性算法呢？是否可以通过改进计数排序、基数排序等来得到一个更高效的算法呢？答案是肯定的。但算法的适用范围会受到一定的限制。

如果所有N个数都是正整数，且它们的取值范围不太大，可以考虑申请空间，记录每个整数出现的次数，然后再从大到小取最大的K个。比如，所有整数都在（0，MAXN）区间中的话，利用一个数组count[MAXN]来记录每个整数出现的个数（count[i]表示整数i在所有整数中出现的个数）。我们只需要扫描一遍就可以得到count数组。然后，寻找第K大的元素：

代码清单2-14

极端情况下，如果N个整数各不相同，我们甚至只需要一个bit来存储这个整数是否存在。

当实际情况下，并不一定能保证所有元素都是正整数，且取值范围不太大。上面的方法仍然可以推广适用。如果N个数中最大的数为V_max，最小的数为V_min，我们可以把这个区间[V_min，V_max]分成M块，每个小区间的跨度为d＝（V_max－V_min）/M，即[V_min，V_min＋d]，[V_min＋d，V_min＋2d]，……然后，扫描一遍所有元素，统计各个小区间中的元素个数，跟上面方法类似地，我们可以知道第K大的元素在哪一个小区间。然后，再对那个小区间，继续进行分块处理。这个方法介于解法三和类计数排序方法之间，不能保证线性。跟解法三类似地，时间复杂度为O（（N＋M）log₂M（|V_max－V_min|/delta））。遍历文件的次数为2log₂M（|V_max－V_min|/delta）。当然，我们需要找一个尽量大的M，但M取值要受内存限制。

在这道题中，我们根据K和N的相对大小，设计了不同的算法。在实际面试中，如果一个面试者能针对一个问题，说出多种不同的方法，并且分析它们各自适用的情况，那一定会给人留下深刻印象。

注：本题目的解答中用到了多种排序算法，这些算法在大部分的算法书籍中都有讲解。掌握排序算法对工作也会很有帮助。

扩展问题

1．如果需要找出N个数中最大的K个不同的浮点数呢？比如，含有10个浮点数的数组（1.5，1.5，2.5，2.5，3.5，3.5，5，0，-1.5，3.5）中最大的3个不同的浮点数是（5，3.5，2.5）。

2．如果是找第k到m（0＜k＜＝m＜＝n）大的数呢？

3．在搜索引擎中，网络上的每个网页都有“权威性”权重，如page rank。如果我们需要寻找权重最大的K个网页，而网页的权重会不断地更新，那么算法要如何变动以达到快速更新（incremental update）并及时返回权重最大的K个网页？

提示：堆排序？当每一个网页权重更新的时候，更新堆。还有更好的方法吗？

4．在实际应用中，还有一个“精确度”的问题。我们可能并不需要返回严格意义上的最大的K个元素，在边界位置允许出现一些误差。当用户输入一个query的时候，对于每一个文档d来说，它跟这个query之间都有一个相关性衡量权重f（query，d）。搜索引擎需要返回给用户的就是相关性权重最大的K个网页。如果每页10个网页，用户不会关心第1000页开外搜索结果的“精确度”，稍有误差是可以接受的。比如我们可以返回相关性第10001大的网页，而不是第9999大的。在这种情况下，算法该如何改进才能更快更有效率呢？网页的数目可能大到一台机器无法容纳得下，这时怎么办呢？

提示：归并排序？如果每台机器都返回最相关的K个文档，那么所有机器上最相关K个文档的并集肯定包含全集中最相关的K个文档。由于边界情况并不需要非常精确，如果每台机器返回最好的K＇个文档，那么K＇应该如何取值，以达到我们返回最相关的90％K个文档是完全精确的，或者最终返回的最相关的K个文档精确度超过90％（最相关的K个文档中90％以上在全集中相关性的确排在前K），或者最终返回的最相关的K个文档最差的相关性排序没有超出110％K。

5．如第4点所说，对于每个文档d，相对于不同的关键字q₁，q₂，…，q_m，分别有相关性权重f（d，q₁），f（d，q₂），…，f（d，q_m）。如果用户输入关键字q_i之后，我们已经获得了最相关的K个文档，而已知关键字q_j跟关键字q_i相似，文档跟这两个关键字的权重大小比较靠近，那么关键字q_i的最相关的K个文档，对寻找q_j最相关的K个文档有没有帮助呢？