1.17　俄罗斯方块游戏

俄罗斯方块（英文：Tetris）是从20世纪80年代开始风靡全世界的电脑游戏。俄罗斯方块是由下面这几种形状的积木块构成，如图1-27所示：

图1-27

如果你说你没玩过Tetris游戏，面试者一定会比较惊讶，不过面试者还是会耐心地跟你解释它的游戏规则：

■　积木块会从游戏区域上方开始缓慢落下。

■　玩家可以做的操作有：90度旋转积木块，左右移动积木块，或者让积木块加速落下。

■　积木块移到游戏区域最下方或是落到其他积木块上无法移动时，就会固定在该处，而之后新的积木块就会出现在区域上方开始落下。

■　当游戏区域中某一行格子全部由积木块填满，则该行会消失并成为玩家的得分。一次删除的行数越多，得分越多。

■　当积木块堆到区域最上方，则游戏结束。

好，现在的问题是：

1．如果你是设计者，如何设计各种数据结构来表示这个游戏的各种元素，如每一个可活动的积木块、在底层堆积的积木等。

2．现在已经知道底层积木的状态，然后在游戏区域上方出现了一个新的积木块，你如何运用刚才设计的数据结构来判断新的积木块要如何移位或旋转，才能最有效率地消除底部累积的积木？

3．有些版本的Tetris游戏有一个预览窗口，从预览窗口可以看到下一个积木块是什么形状。玩家这时候就可以提前计划，比如，如果下一个积木块是一根长条，我们就不要把最深的“峡谷”堵住。那么我们有了这个新的参数，如何改写上一个程序，才能最有效率地消除底部累积的积木？

分析与解法

俄罗斯方块的确是非常经典的游戏，网络上常常出现高手的游戏视频，他们的表现让人叹为观止。如果你是一个俄罗斯方块高手，那你几乎不用思考，让直觉指导自己下一步怎么操作。电脑没有直觉，它只能当一个初学者，所以我们必须为它找到一种可操作的流程。

每一块积木块落下的过程中，我们可以做：

■　旋转到合适的方向

■　水平移动到某一列

■　垂直下落到底部

对于高手来说，下落的过程中还可以有更多精彩的表现，比如平移方块“钻”进洞里去（如图1-28所示）。我们暂时不考虑这种特殊情况。

图1-28

现在可以考虑用怎样的数据结构来模拟积木块下落的过程。

首先，用一个二维数组area[M][N]表示M*N的游戏区域。其中，数组中值为0表示空，1表示有方块。

积木块也用数组来表示，但是各种积木块的尺寸都不相同（如长条是1×4的，方块是2×2的），而且旋转后的尺寸也可能发生变化，如果为不同的积木块设计不同尺寸的数组，则可能造成程序管理的混乱。因此我们需要用统一尺寸的数组来容纳所有可能的积木块，4×4的数组（图1-29表示了五种积木）可以满足要求。

图1-29

积木块一共有7种，每种积木块有4种方向。综上所述，定义BlockSets[7][4][4][4]，表示7种积木块的4个旋转方向的形状。我们在编译前将这个数组的值预计算好，在程序中即可直接使用。

读者一定会发现有些积木块实际上只有两种旋转方式，为了减少程序中的判断条件，我们依然采用适当浪费内存的方法。

使用上面的数据结构，能够很方便地得到方块旋转后的形状rotatedBlock＝BlockSets[n][m％4]，其中n是特定的方块序号，m是旋转的次数。

接下来的问题是判断方块的水平移动范围，我们记录积木块左上角相对于游戏区域的位移为（offset X，offset Y），平移范围即为Offset X的取值范围。

由于积木块可能无法占满4×4区域的每一列，因此横向位移x的值可能小于0。首先计算积木块所占区域的最小列minCol和最大列maxCol，则Offset X的取值范围为[0－minCol，M－1－maxCol]。图1-30中，L型积木块占据的最小列和最大列分别为1和2。因此，这个积木块在游戏区域里面水平移动的范围为[-1，N－3]。

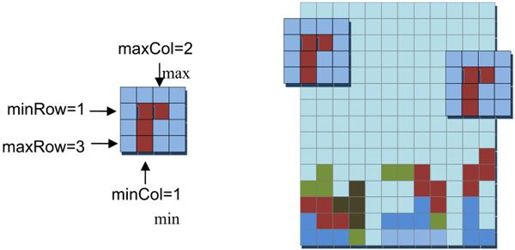
图1-30

有了位移坐标，就很容易计算出积木块是否和游戏区域中已有的方块重叠。与minCol和maxCol一样，定义minRow和maxRow为积木块所占区域的最小行和最大行。因此下落过程可以表示为：

代码清单1-28

这是一个可行的算法，但是效率比较低。因为每下落一行，很多区域都需要重复判断。有没有更有效的方法呢？以图1-31的所示L型积木块为例，希望其下落在Offset X＝3这一列。我们发现，可以下落到的最低高度取决于最先接触到已有方块那一列。由此，可以计算每一列触底高度的最小值，即min_0≤i≤3（d_i－maxRow_i），其中d_i是该列堆积方块的高度。

在图1-31中，L型积木块第0列和第3列没有方块，则无须考虑；第1列和第2列maxRow分别为3和1。游戏区域第4列和第5列的最高高度分别为N和N－5。因此，积木块将下落到的高度为min（N－3，N－5－1）＝N－6，即L型积木块会停留在位移（3，M－6）的位置。

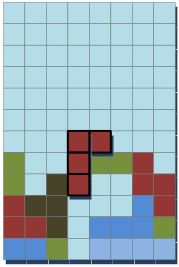
图1-31

由此，已经能够模拟一个方块的下落过程。通过枚举的方法，能够得到积木块在各种旋转角度下，在各列下落的格局。

代码清单1-29

现在离“自动摆放”的人工智能只有一步之遥——判断哪一种格局更好。

世界上举办过俄罗斯方块人工智能的竞赛，两个选手分别使用自己写的智能模块操作积木块，看谁的程序能够在指定时间内得到更多的分数。在此我们仅给出一种启发性的思路，而不给出具体的解法。

当你问一个俄罗斯方块玩家怎样摆放算是好的，他一般会建议：一次性多消行，不要形成“洞”（图1-32中斜线部分），争取不要摆放太高。作为一个自然人，你能够理解他的意思。但是，计算机对这种感性的语言没有理解能力，没办法要求它用感性的方法回答哪种摆放比较好，因此需要将格局的好坏用一种量化的方法表示出来。

我们采用“计分制”，具体来讲就是如果这种摆放达到了某要求就增加某一指定的分数，反之扣除。举例来说，如果这种摆放可以消除2行，则加上3分；如果形成了5个“洞”则扣除20分。

图1-32

高手的建议可以用如下的计分方法量化：

■　一次性多消行：同时消除1，2，3，4行，分别加1，3，7，13分（分数指数上升）；

■　不要形成“洞”：每增加1个洞，扣除4分，超过5个洞，额外扣除15分；

■　争取不要摆放太高：放置行高于M*3/5，则每高1行则扣除2分。

上述的分数是自己估计的，读者可以根据实际情况来调整，达到一个最佳智能状况。下面是实现上述计分规则的伪代码：

代码清单1-30

先使用这个方法为每种不同格局打一个分数，然后取分数最高的格局作为放置积木块的位置。

当然，实际的计分规则应该更复杂，比如尽量保留某一列为空，等长条来时消4行；或者，统计各种不同积木块出现的数量，预测后面可能出现何种积木块的概率比较大，等等。读者可以充分发挥自己的想象力来创造更好的计分规则。

如果我们可以预知下一块的形状，这个问题就稍微复杂了一些。好在俄罗斯方块的游戏区域并不大，还是能够穷举各种不同的摆放，然后同样使用“计分制”将最好的格局选择出来。要注意，摆放第二块积木前，第一块积木可能会消行，因此需要额外的空间来处理。

更进一步，如果预知下面多块的形状，穷举的方法依然适用，但是复杂度呈指数级别上升，所以需要用“减枝”的方法来降低复杂度。简单地说，就是穷举一个积木块的各种格局后，计算每种格局的得分，然后只取前N个最高得分的格局进行后续计算。这种方法是合理的：如果一个格局本身就很糟，那么在这个格局的基础上继续摆放也不会好到哪里去。但是，如果N设置的较小，则可能会漏掉最优解。因此需要根据实际情况调整N的取值。

扩展问题：

1．如果希望支持在下落过程中水平移动来“钻洞”，那么程序流程需要怎么调整？

2．如图1-33所示，我们假设积木块在自动下落过程中，每两次自动下落间最多水平移动三格，那么该积木块是无法到达区域最右侧的。如果增加了这个限制，程序流程需要怎么调整？

3．俄罗斯方块，挖雷等游戏为什么这么流行？如果面试者让你给这些游戏增加一些新功能，你能否在有限的时间内提出想法，并且说服对方？

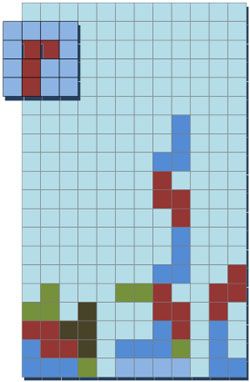
图1-33