2.13　子数组的最大乘积

给定一个长度为N的整数数组，只允许用乘法，不能用除法，计算任意（N－1）个数的组合乘积中最大的一组，并写出算法的时间复杂度。

我们把所有可能的（N－1）个数的组合找出来，分别计算它们的乘积，并比较大小。由于总共有N个（N－1）个数的组合，总的时间复杂度为O（N²），但显然这不是最好的解法。

分析与解法

【解法一】

在计算机科学中，时间和空间往往是一对矛盾体，不过，这里有一个优化的折中方法。可以通过“空间换时间”或“时间换空间”的策略来达到优化某一方面的效果。在这里，是否可以通过“空间换时间”来降低时间复杂度呢？

计算（N－1）个数的组合乘积，假设第i个（0≤i≤N－1）元素被排除在乘积之外（如图2-13所示）。

图2-13组合示意图

设array[]为初始数组，s[i]表示数组前i个元素的乘积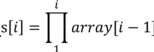，其中1≤i≤N，s[0]＝1（边界条件），那么s[i]＝s[i－1]×array[i－1]，其中i＝1，2，…，N－1，N；

设t[i]表示数组后（N－i）个元素的乘积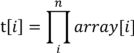，其中1≤i≤N，t[N＋1]＝1（边界条件），那么t[i]＝t[i＋1]×array[i]，其中i＝1，2，…，N－1，N；

那么设p[i]为数组除第i个元素外，其他N－1个元素的乘积，即有：

p[i]＝s[i－1]×t[i＋1]。

由于只需要从头至尾，和从尾至头扫描数组两次即可得到数组s[]和t[]，进而线性时间可以得到p[]。所以，很容易就可以得到p[]的最大值（只需遍历p[]一次）。总的时间复杂度等于计算数组s[]、t[]、p[]的时间复杂度加上查找p[]最大值的时间复杂度等于O（N）。

【解法二】

其实，还可以通过分析，进一步减少解答问题的计算量。假设N个整数的乘积为P，针对P的正负性进行如下分析（其中，A_N－1表示N－1个数的组合，P_N－1表示N－1个数的组合的乘积）：

1．P为0

那么，数组中至少包含有一个0。假设除去一个0之外，其他N－1个数的乘积为Q，根据Q的正负性进行讨论：

Q为0

说明数组中至少有两个0，那么N－1个数的乘积只能为0，返回0；

Q为正数

返回Q，因为如果以0替换此时A_N－1中的任一个数，所得到的P_N－1为0，必然小于Q；

Q为负数

如果以0替换此时A_N－1中的任一个数，所得到的P_N－1为0，大于Q，乘积最大值为0。

2．P为负数

根据“负负得正”的乘法性质，自然想到从N个整数中去掉一个负数，使得P_N－1为一个正数。而要使这个正数最大，这个被去掉的负数的绝对值必须是数组中最小的。我们只需要扫描一遍数组，把绝对值最小的负数给去掉就可以了。

3．P为正数

类似P为负数的情况，应该去掉一个绝对值最小的正数值，这样得到的P_N－1就是最大的。

上面的解法采用了直接求N个整数的乘积P，进而判断P的正负性的办法，但是直接求乘积在编译环境下往往会有溢出的危险（这也就是本题要求不使用除法的潜在用意☺），事实上可做一个小的转变，不需要直接求乘积，而是求出数组中正数（+）、负数（-）和0的个数，从而判断P的正负性，其余部分与以上面的解法相同。

在时间复杂度方面，由于只需要遍历数组一次，在遍历数组的同时就可得到数组中正数（+）、负数（-）和0的个数，以及数组中绝对值最小的正数和负数，时间复杂度为O（N）。