2.19　区间重合判断

给定一个源区间[x，y]（y≥x）和N个无序的目标区间[x₁，y₁][x₂，y₂][x₃，y₃]…[x_n，y_n]，判断源区间[x，y]是不是在目标区间内（也即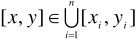是否成立）？

例如：给定源区间[1，6]和一组无序的目标区间[2，3][1，2][3，9]，即可认为区间[1，6]在区间[2，3][1，2][3，9]内（因为目标区间实际上是[1，9]）。

分析与解法

【解法一】

问题的本质在于对目标区间的处理。一个比较直接的思路即将源区间[x，y]（y≥x），和N个无序的目标区间[x₁，y₁][x₂，y₂][x₃，y₃]…[x_n，y_n]逐个投影到坐标轴上，只考察源区间未被覆盖的部分。如果所有的目标区间全部投影完毕，仍然有源区间没有被覆盖，那么源区间就不在目标区间之内。

仍以[1，6]和[2，3][1，2][3，9]为例，考察[1，6]是否在[2，3][1，2][3，9]内：

源区间为[1，6]，那么最初未被覆盖的部分为{[1，6]}（如图2-19所示），将按顺序考察目标区间[2，3][1，2][3，9]：

图2-19

将目标区间[2，3]投影到坐标轴，那么未被覆盖的部分{[1，6]}将变为{[1，2]，[3，6]}（如图2-20所示）：

图2-20

将目标区间[1，2]投影到坐标轴，那么未被覆盖的部分{[1，2]，[3，6]}将变为{[3，6]}（如图2-21所示）：

图2-21

将目标区间[3，9]投影到坐标轴，那么未被覆盖的部分{[3，6]}将变为{φ}，即可说明[1，6]是在[2，3][1，2][3，9]内（如图2-22所示）！

图2-22

由以上步骤可看出，每次操作，尚未被覆盖的区间数组大小最多增加1（当然可能减少），而每投影一个新的目标区间，计算有哪些源区间数组被覆盖需要O（log₂N）的时间复杂度，但是更新尚未被覆盖的区间数组需要O（N）的时间复杂度，所以总的时间复杂度为O（N²）。

这个解法的时间复杂度高，而且如果要对k组源区间进行查询，那么时间复杂度会增大单次查询的k倍。有没有更好的解法，使得单次查询的时间复杂度降低，并且使k次查询的时间复杂度小于单次查询的时间复杂度的1/k倍呢？

【解法二】

一种值得尝试并已经在本书中多次运用的思路是，对现有的数组进行一些预处理（如合并、排序等），将无序的目标区间合并成几个有序的区间，这样就可以进行区间的比较。

因此，问题就变成了如何将这些无序的数组转化为一个目标区间。

首先可以做一次数据初始化的工作。由于目标区间数组是无序的，因此可以对其进行合并操作，使其变得有序。

即先将目标区间数组按X轴坐标从小到大排序（排序时可采用快速排序等），如[2，3][1，2][3，9]→[1，2][2，3][3，9]；接着扫描排序后的目标区间数组，将这些区间合并成若干个互不相交的区间，如[1，2][2，3][3，9]→[1，9]。

然后在数据初始化的基础上，运用二分查找（为什么？）来判定源区间[x，y]是否被合并后的这些互不相交的区间中的某一个包含。如[1，6]被[1，9]包含，则可说明[1，6]在[2，3][1，2][3，9]内。

这种思路相对简单，时间复杂度计算如下：

排序的时间复杂度：O（N*log₂N）（N为目标区间的个数）；

合并的时间复杂度：O（N）；

单次查找的时间复杂度：log₂N；

所以总的时间复杂度为O（Nlog₂N）＋O（N）＋O（klog₂N）＝O（Nlog₂N＋klog₂N），k为查询的次数，合并目标区间数组的初始化数据操作只需要进行一次。

这样不仅单次查询的时间复杂度降低了，而且对于k＞＞N的情况，处理起来也会方便很多。

总结

解法一采用利用目标区间来分割源区间的方法，会增加存储空间；解法二采用合并的方法，既简单又节省了空间。

扩展问题

如何处理二维空间的覆盖问题？例如在Windows桌面上有若干窗口，如何判断某一窗口是否完全被其他窗口覆盖？