4.3　买票找零

在一场激烈的足球赛开始前，售票工作正在紧张地进行中。每张球票为50元。现有2n个人排队购票，其中有n个人手持50元的钞票，另外n个人手持100元的钞票，假设开始售票时售票处没有零钱。问这2n个人有多少种排队方式，不至使售票处出现找不开钱的局面？

分析与解法

【解法一】

从题目中可以推断出，只有手持100元的人才需要找50元。也就是说，当手持100元的球迷到达售票处时，售票处至少要有一张50元的零钱。不难看出，从队首开始往后数，任何时候，只要手持100元的球迷总比手持50元的球迷少，肯定可以把钱找开。

从这个问题可以联想到括号匹配问题。假设每个手持50元的球迷是一个左括号“（”，而手持100元的球迷是右括号“）”，要求任意一个左括号都要有一个右括号跟它对应。类似的，任意一个手持100元的球迷，他从售票处找回的50元都来自于他之前一个手持50元的球迷。所以，始终找得开钱的排队方式对应着合法的括号排列。

根据解决括号匹配问题的思路，可以考虑用栈来解决问题。假设存在一个栈，遍历n个左括号“（”和n个右括号“）”排成的队列，每次如果是左括号“（”（手持50元的球迷），则将其压入栈中；如果是右括号“）”（手持100元的球迷），则让栈尾的左括号“（”（手持50元的球迷）出栈，如果始终能够保证栈中有足够的左括号，那么该排列是一个合法的排列。

因此，可以做这样的分析。第一个符号一定是左括号，否则该队列肯定出错。假设第一个左括号跟第k个符号匹配。那么从第2个符号到第（k－1）个符号，第（k＋1）个符号到第2n个符号也都是一个合法的括号序列。可想而知，k肯定是奇数。否则，第2个符号到第（k－1）个符号之间只有奇数个符号就不合法，设k＝2i＋1（i＝0，…，n－1）。

如图4-3所示：

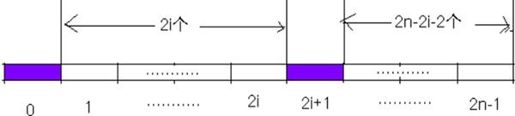
图4-3　括号排列示意图

假设2n个符号中合法的括号序列之个数为f（2n），若第一个左括号与第k＝2i＋1（i＝0，1，…，n－1）个右括号匹配，那么剩余括号的合法序列为：f（2i）*f（2n－2i－2）个，根据上面的分析，可以得到如下递推式：

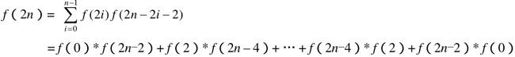
（其中f（0）＝1）。这样我们可以用O（n*n）的时间求出问题的答案。

我们可以根据上述递推式，进一步得到通项公式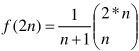：，又称Catalan数。我们并不打算在这里讲解如何推导出这个公式，但会用另一种解法得到同样的答案。

【解法二】

为了便于描述，这里用1表示持有50元的球迷，用0表示持有100元的球迷。那么2n个球迷的排队就对应n个1和n个0的排列，例如：1，1，0，0，0，…，1。如果序列的任意前k（k＝1，2，…，2n－1）项中1的个数都不少于0的个数，我们称这样的一个序列是合法的，否则称其为非法的。显然合法的序列正好与可行的排列方式一一对应。同时，称由n－1个1和n＋1个0组成的序列为Sigma序列（这个名字没有任何特别的意义），这样的序列共有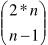个，我们会在后面用到。

n个1和n个0总的排列数为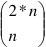（2n个位置，选择n个给1，剩下的n个给0就可以了），即合法序列数和非法序列数的总和。我们需要求解合法的序列数，但在尝试后会发现直接求解合法序列并不是一个好的主意，那就试着来求解非法序列吧。

由定义知道，在一个非法序列中，存在某个（些）k，使得序列前k项中1的个数少于0的个数。更进一步地，存在某个（些）k，使得序列前k项中1的个数比0的个数刚好少1个（想一想为什么）。取其中最小的k，使得前k项中1的个数比0的个数刚好少1个。那么这个序列的后2n－k项中1的个数会刚好比0的个数多1个。将后2n-k项的0换为1，1换为0，于是得到一个新的序列：由n－1个1和n＋1个0组成一个Sigma序列。我们已经成功地将一个非法序列对应到唯一一个Sigma序列。

那么一个Sigma序列能唯一地对应到一个非法序列么？对任意一个Sigma序列，存在某个（些）k，使得序列的前k项中1的个数少于0的个数（因为只有n－1个1，而有n＋1个0）。更进一步地，存在某个（些）k，使得序列的前k项中1的个数比0的个数刚好少1个（想一想这又是为什么）。取其中最小的k，使得前k项中1的个数比0的个数刚好少1个。那么这个序列的后2n－k项中1的个数会刚好比0的个数少1个。将后2n－k项的0换为1，1换为0，于是得到一个新的序列：由n个1和n个0组成。而这个序列正是一个非法的序列（因为前k项中1的个数比0少）。我们又成功地将一个Sigma序列对应到唯一一个非法序列。

由此我们知道，非法序列和Sigma序列是一一对应的。非法的序列个数为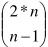；合法的序列数，也就是可行的排队方式数则为：。

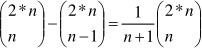扩展问题

1．矩阵连乘问题：P＝a₁×a₂×a₃×…×a_n，依据乘法结合律，不改变矩阵的相互顺序，只用括号表示成对的乘积，试问有几种括号化的方案？

2．将多边形划分为三角形问题。求一个凸多边形区域划分成三角形区域的方法数。

与此题类似的题目1：某个城市的某个居民，每天他需要走2n个街区去上班（他在其住所以北n个街区和以东n个街区处工作）。如果他从不穿越（但可以碰到）从家到办公室的对角线，那么有多少条可能的道路？

与此题类似的题目2：在圆上选择2n个点，将这些点成对连接起来，求使所得到的n条线段不相交的方法数。

3．n个结点可构造多少个不同的二叉树。