3.8　求二叉树中节点的最大距离

如果我们把二叉树看成一个图，父子节点之间的连线看成是双向的，我们姑且定义“距离”为两个节点之间边的个数。

写一个程序求一棵二叉树中相距最远的两个节点之间的距离。

如图3-11所示，粗箭头的边表示最长距离：

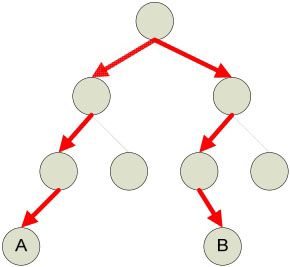
图3-11　树中相距最远的两个节点A，B

分析与解法

我们先画几个不同形状的二叉树，（如图3-12所示），看看能否得到一些启示。

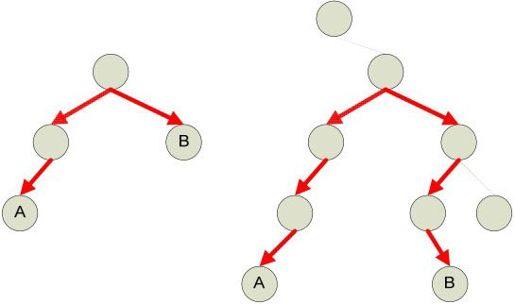
图3-12　几个例子

从例子中可以看出，相距最远的两个节点，一定是两个叶子节点，或者是一个叶子节点到它的根节点。（为什么？）

【解法一】

根据相距最远的两个节点一定是叶子节点这个规律，我们可以进一步讨论。

对于任意一个节点，以该节点为根，假设这个根有K个孩子节点，那么相距最远的两个节点U和V之间的路径与这个根节点的关系有两种情况：

1．若路径经过根Root，则U和V是属于不同子树的，且它们都是该子树中到根节点最远的节点，否则跟它们的距离最远相矛盾。这种情况如图3-13所示：

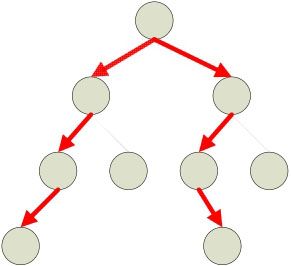
图3-13　相距最远的节点在左右最长的子树中

2．如果路径不经过Root，那么它们一定属于根的K个子树之一。并且它们也是该子树中相距最远的两个顶点。如图3-14中的节点A：

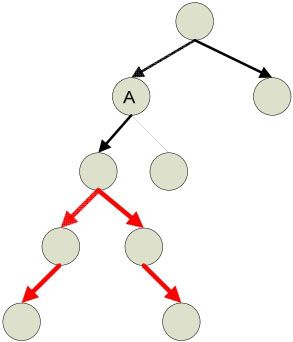
图3-14　相距最远的节点在某个子树下

因此，问题就可以转化为在子树上的解，从而能够利用动态规划来解决。

设第K棵子树中相距最远的两个节点：U_k和V_k，其距离定义为d（U_k，V_k），那么节点U_k或V_k即为子树K到根节点R_k距离最长的节点。不失一般性，我们设U_k为子树K中到根节点R_k距离最长的节点，其到根节点的距离定义为d（U_k，R）。取d（U_i，R）（1≤i≤k）中最大的两个值max1和max2，那么经过根节点R的最长路径为max1＋max2＋2，所以树R中相距最远的两个点的距离为：max{d（U₁，V₁），…，d（U_k，V_k），max1＋max2＋2}。

采用深度优先搜索如图3-15，只需要遍历所有的节点一次，时间复杂度为O（|E|）＝O（|V|－1），其中V为点的集合，E为边的集合。

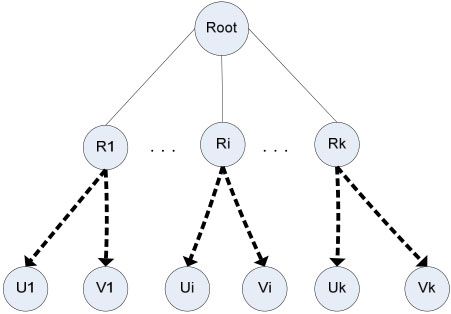
图3-15　深度遍历示意图

示例代码如下，我们使用二叉树来实现该算法。

代码清单3-11

扩展问题

在代码中，我们使用了递归的办法来完成问题的求解。那么是否有非递归的算法来解决这个问题呢？

总结

对于递归问题的分析，笔者有一些小小的体会：

1．先弄清楚递归的顺序。在递归的实现中，往往需要假设后续的调用已经完成，在此基础之上，才实现递归的逻辑。在该题中，我们就是假设已经把后面的长度计算出来了，然后继续考虑后面的逻辑；

2．分析清楚递归体的逻辑，然后写出来。比如在上面的问题中，递归体的逻辑就是如何计算两边最长的距离；

3．考虑清楚递归退出的边界条件。也就说，哪些地方应该写return。

注意到以上3点，在面对递归问题的时候，我们将总是有章可循。