2.10　寻找数组中的最大值和最小值

数组是最简单的一种数据结构。我们经常碰到的一个基本问题，就是寻找整个数组中最大的数，或者最小的数。这时，我们都会扫描一遍数组，把最大（最小）的数找出来。如果我们需要同时找出最大和最小的数呢？

对于一个由N个整数组成的数组，需要比较多少次才能把最大和最小的数找出来呢？

分析与解法

【解法一】

可以把寻找数组中的最大值和最小值看成是两个独立的问题，我们只要分别求出数组的最大值和最小值即可解决问题。最直接的做法是先扫描一遍数组，找出最大的数以及最小的数。这样，我们需要比较2*N次才能找出最大的数和最小的数。

能否在这两个看似独立的问题之间建立关联，从而减少比较的次数呢？

【解法二】

一般情况下，最大的数和最小的数不会是同一个数（除非N＝1，或者所有整数都是一样的大小）。所以，我们希望先把数组分成两部分，然后再从这两部分中分别找出最大的数和最小的数。

首先按顺序将数组中相邻的两个数分在同一组（这只是概念上的分组，无须做任何实际操作）。若数组为{5，6，8，3，7，9}（如图2-5所示）：

图2-5　数组示意图

接着比较同一组中奇数位数字和偶数位数字，将较大的数放在偶数位上，较小的数放在奇数位上。经过N/2次比较的预处理后，较大的数都放到了偶数位置上，较小的数则放到了奇数位置上，如图2-6所示：

图2-6

最后，我们从奇偶数位上分别求出Max＝9，Min＝3，各需要比较N/2次。整个算法共需要比较1.5*N次。

【解法三】

解法二已经将比较次数降低到了1.5*N次，但它破坏了原数组，如何能够不破坏原数组呢？解法二是事先将两两分组中较小和较大的数调整了顺序，从而破坏了数组，如果可以在遍历的过程中进行比较，而不需要对数组中的元素进行调换，就可以不用破坏原数组了。首先仍然按顺序将数组中相邻的两个数分在同一组（这只是概念上的分组，无须做任何实际操作）。然后可以利用两个变量Max和Min来存储当前的最大值和最小值。同一组的两个数比较之后，不再调整顺序，而是将其中较小的数与当前Min作比较，如果该数小于当前Min则更新Min。同理，将其中较大的数与当前Max作比较，如果该数大于当前Max，则更新Max。如此反复比较，直到遍历完整个数组。Min和Max分别被初始化为数组第一和第二个数中的小者和大者。仍设原数组为{5，6，8，3，7，9}，则Min和Max分别被初始化为6和5。比较过程如图2-7所示：

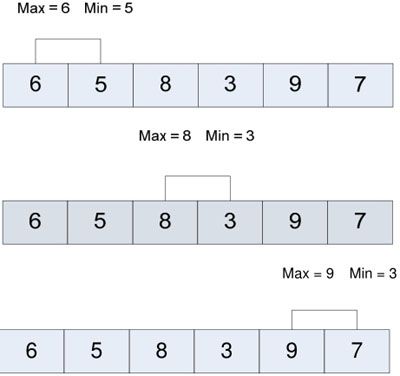
图2-7　查找比较示意图

最后，Max＝9，Min＝3。但是时间复杂度并未降低，整个过程的比较次数仍为1.5*N次。

【解法四】

分治思想是算法中很常用的一种技巧。在N个数中求最小值Min和最大值Max，我们只须分别求出前后N/2个数的Min和Max，然后取较小的Min，较大的Max即可（只须较大的数和较大的数比较，较小的数和较小的数比较，两次就可以了）。

假设我们要求arr[1，2，…，n]数组的最大数和最小数，上述算法的伪代码则为：

代码清单2-20

如果用f（N）表示这个算法对于N个数的情况需要比较的次数。我们可以得到：

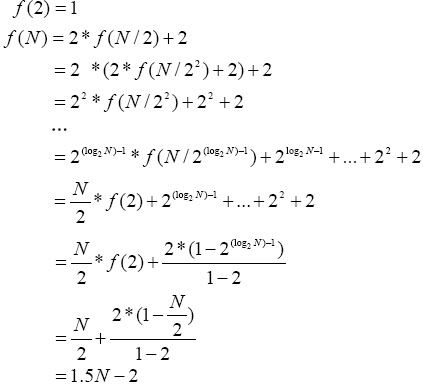
所以说即使采用分治法，总的比较次数仍然没有减少。

扩展问题

如果需要找出N个数组中的第二大数，需要比较多少次呢？是否可以使用类似的分治思想来降低比较的次数呢？