4.9　数独知多少

通过前面的题目（1.15节“构造数独”）的介绍，相信大家都已经很熟悉数独游戏了，我们还有几个“小”问题没有解决。

图4-12是一个已完成的数独，可以看出，图中每一行、每一列和九个3×3的小矩阵都没有重复的数字出现。

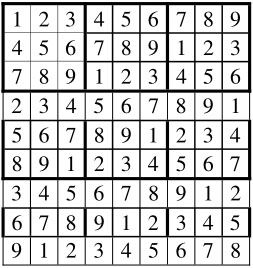
图4-12

图4-13是另一个填好的数独：

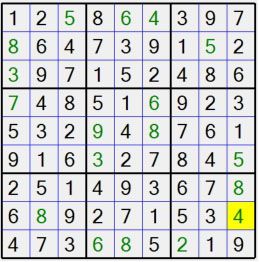
图4-13

问题

一共有多少种不同的数独解答呢？其中有多少种是独立的解答呢？

如果我们要用一个简单的字符串来表示各种数独（例如：上面的数独可以用“125864…685219”来表示），如何在保证一一对应的基础上，让字符串的长度最短？

分析与解法

那么有多少种数独的解答呢？在这些解答中，独立的解答有多少呢？现在我们假设面试者给你出了这个问题，你也许会想——啊呀，如果我提前背下“数独总数”这个答案和证明就好了……

其实，面试者不是在考你的记忆力，面试者要看到的是应聘者如何思考，如何着手解决有挑战性的问题。

很多应聘者听到这个问题，就陷入了沉思，或者急忙开始演算。其实解决问题的第一步，就是要明确问题到底是什么，这和做软件项目类似——如果客户告诉你：“我想做一个网站……”

你不会马上打断用户：“好！不要再说了，你回去吧，三个月后网站交付！”你会进一步去问，什么样的网站？网站要解决什么问题？用户是谁？类似的网站有那些……

同样，对于“数独的所有解答”这一问题，你应该反问：“‘独立＇是什么意思？所有解答是精确到个位数的答案，还是一个估计值？”

谈到“独立”，就要研究独立的定义。我们可以看出，任意交换数独的两个数字（例如：上图中所有“1”都变成“9”，同时“9”都变成“1”），得到的仍是一个合法的数独解答。那么，我们可以定义：如果两个数独解答可以通过这样方式转换得到对方，则它们不是独立的。

基于上述的定义，每个数独解答都可以通过上述的转化，把它们九宫格的左上3×3小格转化为图4-14的“标准型”：

图4-14

不考虑是否独立的情况下，一个空的数独有N个解答，那么考虑了上述的等价关系之后，独立的解答数目应该是N/（9！）。^③

关于解答的总数，面试者想要的其实只是一个近似的答案。如果应聘者能够在短时间内通过分析，把大问题分解为若干个子问题，然后推导出这个答案的上界和下界，就算很不错了^④。

我们在这里展示一种用探索（heuristic）的方法估计解答总数的思路。数独的9个子块标记如图4-15所示：

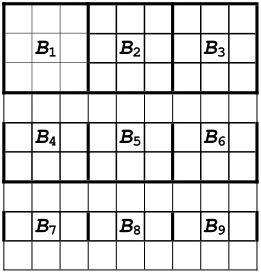
图4-15

为了方便讨论，称B₁、B₂和B₃组成一个“块行”，如果一个解使得“块行”内每行每块都恰好包含1到9这九个数字，则称该解为一个“块行解”；称B₁、B₄和B₇组成一个“块列”，如果一个解使得“块列”内每列每块都恰好包含1到9这九个数字，则称该解为一个“块列解”；如果九个数字在一个块内按如下方式排列，则称其为“标准型”（如图4-16所示）：

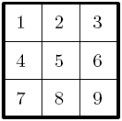
图4-16

首先讨论有多少组“块行解”。假设B₁是“标准型”，一旦我们能得到一个基于B₁“标准型”的“块行解”，我们就能通过一个1到9的“置换”得到另一个“块行解”（“置换”是指每个数字都变化为1到9中的一个数字，变化后的数字依然是1到9，九个不重复的数字）。显然这样的“置换”共有9！个，所以如果基于B₁“标准型”的“块行解”有N个，则“块行解”总共有9！*N个。

下面讨论基于B₁“标准型”的“块行解”个数。B₂和B₃第一行的构成有两种可能性：由B₁的第二行或第三行构成（“纯粹型”），或者由B₁第二行第三行混合构成（“混合型”）。“纯粹型”如图4-17：

图4-17

每一行中的3个元素都可以任意交换，并且B₂和B₃位置也可以交换，所以共有2*（3！）⁶。“混合型”如图4-18：

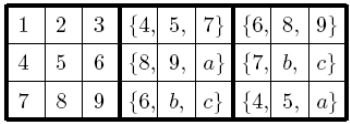
图4-18

其中a、b、c表示1、2、3所在位置，a可以是1、2、3中的任何一个数，每一行中的3个元素都可以任意交换，B₂和B₃位置可以交换，此外B₂和B₃的第一行共有如下九种可能性：

所以共有3×2×9×（3！）⁶。因此“块行解”共有9！×（2×（3！）⁶＋3×2×9×（3！）⁶）＝948109639680。同理，“块列解”也有948109639680组解。

满足每个子块都由1到9填充的解共有N＝（9！）⁹。“块行解”有948109639680，九宫格内有三个“块行”，所以满足每行每块都由1到9填充的解共有M＝948109639680³。满足块行限制解在满足块限制解中所占的比例为k＝M/N。同理满足块列限制解在满足块限制解中所占比例也为k＝M/N。假设以上两个比例相互独立（事实上它们并不完全独立），则同时满足块行列限制解在满足块限制解中所占比例约为k²，因此同时满足块行列限制的解（即空九宫格的解）总数约为N×k²＝948109639680⁶/（9！）9～6.6571×10²¹。该估计结果与精确结果6.671×10²¹相差大约0.2％。^⑤

再考虑第三个问题，如果现在有一个数独答案，我们怎么记录这个答案呢？最直接的方法我们可以从上到下，从左到右记录每一个数字。比如对于图4-19：

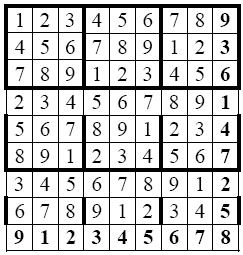
图4-19

数独可以记录为：

123456789456789123789123456234567891567891234891234567345678912678912345912345678。

每个数字用一个char来存储的话，需要空间81byte。如果用4bit表示一个数字，仍需要40.5byte。

你也许很快可以发现，我们只需要记录数独的左上8×8方阵中的64个数字，其他17个数字必然可以从这64个数字中推出来。这样，我们还使用上述最简单编码，则只需要32byte，记录数独为：

1234567845678912789123452345678956789123891234563456789167891234。

肯定还有很多可以进一步压缩空间的，例如每一个数字（1～9）可以用4个位就可以表示，又比如，如果12是相邻两个数字，它们可以当作整数“12”而不造成歧义，两个数字才需要4bit。各种方法不一而足。那么，最少需要多少空间呢？也就是这个问题的下界是多少呢？

在上一个问题中，聪明的读者可能已经找到答案，不考虑等价的情况下，有6670903752021072936960（6.7×10²¹）个不同的数独。如果我们使用k bit空间，我们最多能表示2^k种不同的数独。那么，我们需要的最少空间至少要能够表示出所有这些数独：

2^k＞6.7×10²¹　　即k＞73，约8byte

我们很好地利用了每一个bit，好处就是节省空间。一般来说，如果找到这样的编码方案，那么这个编码译码算法的难度会比上面的方案复杂。读者可以继续寻找更加节省空间的编码方案。

扩展问题

如果要编码表示一个不完全的数独（如图4-20所示），什么方法比较好？能否写程序实现你的算法？

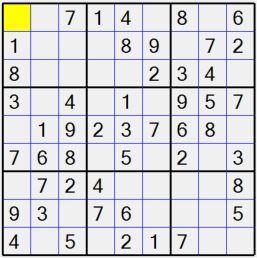
图4-20