4.5　磁带文件存放优化

磁带是一种线性存储设备，一个文件在磁带上的存储区域是完整而且连续的，而多个文件的存储区域是相互独立且连续分布的，如图4-9所示。与今天大量使用的磁盘式存储设备不同，磁带没有扇区、柱面、磁道等概念，所以在进行文件寻址时需要耗费线性时间，即要定位到磁带上的第n个文件，需要依次经过前面的n－1个文件的磁带长度。如今，磁盘式存储设备一般能以低于线性时间的效率进行寻址，但是磁带式存储设备因其低廉的价格，简单的存储结构以及海量的存储空间，在今天依然被许多数据中心选为数据备份设备。

图4-9　文件在磁带上呈线性分布

大型的数据中心一般会采用一个磁带SAN（Storage Area Network，存储区域网络）作为备份设备（如图4-10所示）。假设其中一盘磁带上有n份文件，它们的长度分别为L[0]，L[1]，…，L[n－1]，且被访问的概率分别为P[0]，P[1]，…，P[n－1]。如果这些文件被访问的概率相等，那么请问怎样安排它们在磁带上的存储顺序最好？

图4-10　一台典型的大型磁带备份设备示意图

分析与解法

首先，我们要考虑的是，何谓“最好”的存储顺序？之前有提到，磁带是一种线性存储设备，对存储于其上的第n个文件的寻址需要先经过前面n－1个文件的磁带长度，时间复杂度为O（N）。那么，如果能找到一种文件存储顺序，使得访问这些文件所需经过的平均磁带长度最短，那么就可以获得“最佳”的访问效率，也就是所谓的“最好”存储顺序。

根据概率论里数学期望的定义，访问这些文件的平均长度为：

如果这些文件被访问的概率相等，即P[i]＝p（i＝0，1，…，n－1），则有：

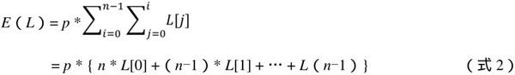
L[j]表示排在第j个位置的文件之长度

P[i]表示排在第i个位置的文件被访问的概率

从式2中可以看出，要让E（L）最小，只要让{nL[0]＋（n－1）L[1]＋…＋L（n－1）}最小即可，也就是让被乘次数最多的文件长度最短，次多的文件长度次短，依次递增文件长度。用一句话来概括，就是按照文件长度由短到长地将文件存储到磁带上，即可得到最佳访问效率。

如果这些文件的长度一样，而访问的概率各不相同，又该按何种存储顺序存储文件呢？

同上一个问题的分析思路一样，我们先求出这些E（L）的表达式，因为L[i]＝l（i＝0，1，…，n－1），有：

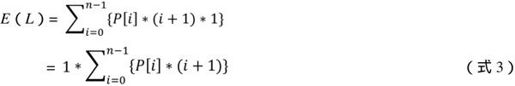
从式3中可以看出，按访问概率从大到小排列文件最好。这样可以保证查找的平均长度最小。

如果文件长度和被访问的概率都不同，何种存储顺序又是最好的呢？

从推导式中可以看出：

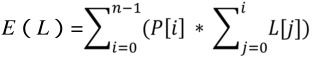
我们可以先用一个具体的例子来计算一下，看看能不能发现什么规律：

假设有两个文件A和B，其长度L分别为10、6，而被访问概率P为0.4、0.6。

那么，把文件B排在文件A前面。这样平均访问长度为0.66＋0.4（6＋10）＝10。

由于我们没有办法直接利用文件的长度和访问概率来进行分析，那么我们可以利用概率／访问长度的关系来进行分析。

对于上述例子来说，第一个文件的P/L＝0.6/6＝0.1，第二种文件的P/L＝0.4/16＝0.025。

而如果文件A在文件B前面，平均访问长度为0.410＋0.6（6＋10）＝13.6。

其中，第一个文件的P/L＝0.4/10＝0.04，第二个文件的P/L＝0.6/16＝0.0375。

同样，我们可以根据上面的推导，判断出P[i]/L[i]的值从大到小排列即为最佳存储顺序。