3.9　重建二叉树

每一个学过算法和数据结构的同学都能很流利地背诵出二叉树的三种遍历次序——前序、中序、后序，也都能很快地写出相应的算法（希望如此），那么，如果已经知道了遍历的结果，能不能把一棵二叉树重新构造出来呢？

给定一棵二叉树，假设每个节点都用唯一的字符来表示，具体结构如下：

假设已经有了前序遍历和中序遍历的结果，希望通过一个算法重建这棵树。

给定函数的定义如下：

参数：

pPreOrder：以null为结尾的前序遍历结果的字符串数组。

pInOrder：以null为结尾的中序遍历结果的字符串数组。

nTreeLen：树的长度。

pRoot：返回node**类型，根据前序和中序遍历结果重新构建树的根节点。

例如：

前序遍历结果：a b d c e f

中序遍历结果：d b a e c f

重建的树如图3-16所示：

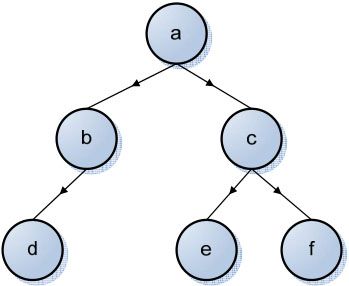
图3-16　重建树示意图

请用C或C++来实现二叉树的重建。

分析与解法

我们先回忆一下定义：

前序遍历：先访问当前节点，然后以前序访问左子树，右子树。

中序遍历：先以中序遍历左子树，接着访问当前节点，然后以中序遍历右子树。

根据前序遍历和中序遍历的特点，可以发现如下规律：

前序遍历的每一个节点，都是当前子树的根节点。同时，以对应的节点为边界，就会把中序遍历的结果分为左子树和右子树。

前序：

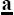b d c e f

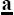“”是根节点

中序：

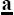d b e c f

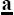“”是根节点，把字符串分成左右两个子树

“a”是前序遍历节点中的第一个元素，可以看出，它把中序遍历的结果分成“db”和“ecf”两个部分。可以从图3-16中看出，这就是“a”的左子树和右子树的遍历结果。

如果能够找到前序遍历中对应的左子树和右子树，就可以把“a”作为当前的根节点，然后依次递归下去，这样就能够把左子树和右子树的遍历结果给依次恢复出来。

确定前序遍历左右子树的这个问题，读者可以在看解法之前自行思考一下。

【解法一】

根据前面的分析，可以通过如下的代码递归解决这个问题。

代码清单3-12

递归的问题可以通过栈或队列的方式来实现。栈或队列的实现相对简单，留给读者自行解决。

扩展问题

1．如果根据字母不能确定节点，换句话说，节点上面的字母有可能是相同的。那么，这道题该如何来做呢？重构出来的二叉树是唯一的吗？如果不是唯一的，如何重构出所有可能的解呢？

2．如何判断给定的前序遍历和中序遍历的结果是合理的呢？

3．如果知道前序和后序遍历的结果，能重构二叉树么？

总结

这个题目可能出现在一些参考书中，有读者看到这道题目之后可能会大失所望地说：“微软也用书上的题目来面试人啊！”

的确，不仅如此，面试者还经常考察排序算法的实现。有不少应聘者不仅不能完整地解答问题，甚至不能描述完整的思路。这样的表现的确对不起在简历上写的“精通算法”等字样。

如果读者自行解答这道题目，一般不会少于20分钟。并且，在编译或调试时，往往还会出现bug。

这些bug通常是怎样产生的呢？

1．边界条件的检查。千万不要认为边界检查不重要，事实上相当重要。

2．没有用实际的例子进行测试。比如说，试验非完全二叉树，退化的二叉树，等等。