3.10　分层遍历二叉树

1．给定一棵二叉树，要求按分层遍历该二叉树，即从上到下按层次访问该二叉树（每一层将单独输出一行），每一层要求访问的顺序为从左到右，并将节点依次编号。那么分层遍历如图3-17中的二叉树，正确输出应为：

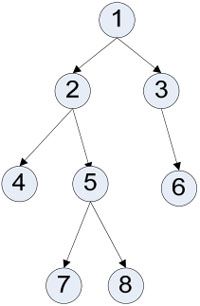
图3-17

2．写另外一个函数，打印二叉树中的某层次的节点（从左到右），其中根节点为第0层，函数原型为int PrintNodeAtLevel（Node*root，int level），成功返回1，失败则返回0。

分析与解法

关于二叉树的问题，由于其本身固有的递归特性，通常我们可以用递归算法来解决。至于题中的两个问题，仔细考虑可以发现，如果解决了第二个问题，则问题1可采用问题2的解法来依次遍历其各层节点。那么我们先来考虑问题2的解法。

首先我们定义节点的数据结构为（设二叉树中的数据类型为整数）：

假设要求访问二叉树中第k层的节点，那么其实可以把它转换成分别访问“以该二叉树根节点的左右子节点为根节点的两棵子树”中层次为k－1的节点，如题目中的二叉树，给定k＝2，即要求访问原二叉树中第2层的节点（根节点为第0层），可把它转换成分别访问以节点2、3为根节点的两棵子树中第k－1＝1层的节点。

代码清单3-13

采用递归算法，思路比较清晰，写出来的代码也很简洁，但缺点就是递归函数的调用效率较低，无论是耗费的计算时间还是占用的存储空间都比非递归算法要多。

以上解决了递归访问二叉树中给定层次节点的问题，那么如何利用该算法来解决问题1呢？如果我们知道该二叉树的深度n，那么只需要调用n次PrintNodeAtLevel()：

代码清单3-14

如果事先不知道二叉树的深度，那么还需要写一个求二叉树的深度的算法，该算法也可用递归实现，有兴趣的读者可以自己试试。但求二叉树深度与问题二是同等时间复杂度的问题，能不能不求二叉树的深度呢？当访问二叉树某一层次失败的时候返回就可以了，代码如下：

代码清单3-15

至此我们解决了题目中的两个问题，但细心的读者可能会发现，其实在问题1的算法中，对二叉树中每一层的访问都需要重新从根节点开始，直到访问完所有的层次。这样的做法，效率实在不高，那么有没有更好的算法呢？

在访问第k层的时候，我们只需要知道第k－1层的节点信息就足够了，所以在访问第k层的时候，要是能够知道第k－1层的节点信息，就不再需要从根节点开始遍历了。

根据上述分析，可以从根节点出发，依次将每层的节点从左到右压入一个数组，并用一个游标Cur记录当前访问的节点，另一个游标Last指示当前层次的最后一个节点的下一个位置，以Cur==Last作为当前层次访问结束的条件，在访问某一层的同时将该层的所有节点的子节点压入数组，在访问完某一层之后，检查是否还有新的层次可以访问，直到访问完所有的层次（不再有新节点可以访问）。

首先将根节点1压入数组，并将游标Cur置为0（游标如图3-18中的箭头所示，数组下标从0开始），游标Last置为1：

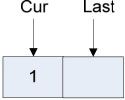
图3-18

Cur＜Last，说明此层（第一层）尚未被访问，因此，依次访问Cur到Last之间的所有节点（第一层只有一个节点），并依次将被访问节点的左右子节点压入数组（注意左右子节点压入数组的顺序），那么访问完第一层的游标及数组的状态如图3-19所示：

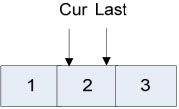
图3-19

由于Cur==Last，说明该层（第一层）已被访问完，此时数组中还有未被访问到的节点，则输出换行符（为输出新的一行做准备），并将Last定位于新一行的末尾（即数组当前最后一个元素的下一位），如图3-20所示：

图3-20

继续依次住下访问其他层次的节点，直到访问完所有的层次（不再有新节点可以访问），如图3-21所示。

图3-21

代码如下：

代码清单3-16

扩展问题

如果要求按深度从下到上访问图3-22中的二叉树，每层的访问顺序仍然是从左到右，即访问顺序变为：

需要如何对算法进行改进？

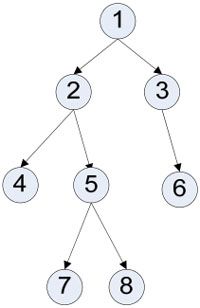
图3-22

提示：可考虑左右节点的访问顺序。

如果按深度从下到上访问，每层的访问顺序变成从右到左，即访问顺序变为：

又需要如何对算法进行改进？