2.9　斐波那契（Fibonacci）数列

斐波那契数列是一个非常美丽、和谐的数列，有人说它起源于一对繁殖力惊人、基因非常优秀的兔子，也有人说远古时期的鹦鹉螺就知道这个规律。

这个数列可以用排成螺旋状的一系列正方形来形象地说明。刚开始，我们把两个边长为1的正方形排列在一起（如图2-2所示）：

图2-2

然后我们依次在图形中边长较长的一边接上一个新的正方形（如图2-3、图2-4所示）：

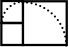
图2-3

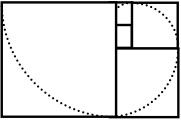
图2-4

按此顺序依次累加，并在新的正方形中加入以边长为半径的圆弧，我们就会得到美丽的曲线。

每一个学理工科的学生都知道斐波那契数列，斐波那契数列由如下递推关系式定义：

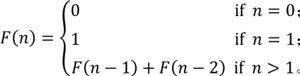
每一个上过算法课的同学都能用递归的方法求解斐波那契数列的第n＋1项的值，即F（n）。

代码清单2-18

我们的问题是：有没有更加优化的解法？

分析与解法

技术面试的一个常见问题是，对于一个常见的算法，能否进一步优化？这个时候，平时喜欢超越课本思考问题的同学，就有施展才华的机会了。

【解法一】递推关系式的优化

上面一页写出的算法是根据递推关系式的定义直接得出的，它在计算F[n]时，需要计算从F[2]到F[n－1]每一项的值，这样简单的递归式存在着很多的重复计算，如求F[5]＝F[4]＋F[3]，在求F[4]的时候也需要求一次F[3]的大小，等等。请问这个算法的时间复杂度是多少？

那么如何减少这样的重复计算呢？可以用一个数组储存所有已计算过的项。这样便可以达到用空间换取时间的目的。在这种情况下，时间复杂度为O（N），而空间复杂度也为O（N）。

那么有更快的算法吗？

【解法二】求解通项公式

如果我们知道一个数列的通项公式，使用公式来计算会更加容易。能不能把这个函数的递推公式计算出来？

由递推公式F（n）＝F（n－1）＋F（n－2），知道F（n）的特征方程为：

x²＝x＋1

有根：

所以存在A，B使得：

代入F（0）＝0，F（1）＝1，解得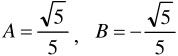

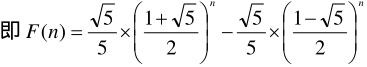
通过公式，我们可以在O（1）的时间内得到F（n）。但公式中引入了无理数，所以不能保证结果的精度。

【解法三】分治策略

注意到Fibonacci数列是二阶递推数列，所以存在一个2*2的矩阵A，使得：

求解，可得：

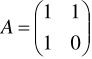
由（1）式我们有：

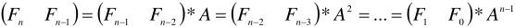
剩下的问题就是求解矩阵A的方幂。

A_n＝AA…*A。最直接的解法就是通过n－1次乘法得到结果。但是当n很大时，比如1000000或1000000000，这个算法的效率就不能接受了。当然，你马上会说，在这个情况下，F_n在整数里早就溢出了，但如果需要求解的是F_n对某个素数的余数呢？这个算法会是非常有用和高效的。

我们注意到：

A^x＋y＝A^x*A^y；

A^x*2＝A^x＋x＝（A^x）²；

用二进制方式表示n：

n＝a_k2^k＋a_k－12^k－1＋…＋a₁*2＋a₀（其中a_i＝0或1，i＝0，1，…，k）；

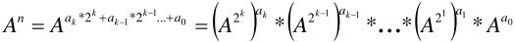
如果能够得到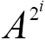（i＝1，2，…，k）的值，就可以再经过log₂n次乘法得到Aⁿ。

而这显然容易通过递推得到：

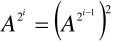
举个例子：

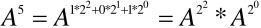
求解：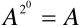

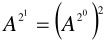
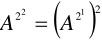
具体的代码如下：

代码清单2-19

整个算法的时间复杂度是O（log₂n）。

扩展问题

假设A（0）＝1，A（1）＝2，A（2）＝2。对于n＞2，都有A（k）＝A（k－1）＋A（k－2）＋A（k－3）。

1．对于任何一个给定的n，如何计算出A（n）？

2．对于n非常大的情况，如n＝2⁶⁰的时候，如何计算A（n）呢？