1.16　24点游戏

24点是一种老少咸宜的游戏，它的具体玩法如下：

给玩家4张牌，每张牌的面值在1～13之间，允许其中有数值相同的牌。采用加、减、乘、除四则运算，允许中间运算存在小数，并且可以使用括号，但每张牌只能使用一次，尝试构造一个多项式，使其运算结果为24。

请你根据上述游戏规则构造一个玩24点游戏的算法，要求如下：

输入：n₁，n₂，n₃，n₄。

输出：若能得到运算结果为24，则输出一个对应的运算表达式。

如：

输入：11，8，3，5

输出：（11－8）×（3＋5）＝24

分析与解法

【解法一】

最直接的想法就是采用穷举法，因为运算符号只有4种，每个数字只能使用一次，所以通过穷举4个数所有可能的表达式，并分别计算出各表达式的值，就可以得到答案。那么如何穷举所有可能的表达式呢？

先不考虑使用括号，可以做出如下分析：

因为每个数只能使用一次，那么就对4个数进行全排列，总共有4！＝4×3×2×1＝24种排列。4个数的四则运算中总共需要3个运算符，同一运算符可以重复出现，那么对于每一个排列，总共可有4×4×4种表达式。因此在不考虑括号的情况下，总共可以得到4！×4³＝1536种表达式。

接下来再考虑加上括号后的情况，对于4个数而言，总共会有以下5种加括号的方式：（A（B（CD））、（A（（BC）D）、（（AB）（CD））、（（A（BC））D）、（（（AB）C）D）。

所以需要遍历的表达式数最多有4！×4³×5＝7680种。当然，这里可以采用逆波兰表达式的方法，但其表达式数仍为4！×4³×5＝7680种。

通过上面的分析，得到了一种解24点的基本思路，即遍历运算符、数字和括号的所有排列组合形式，接下来，我们将更加细致地讨论这种解法的一个具体实现。

假设给定的4个数组成的集合为A＝{1，2，3，4}，定义函数f（A）为对集合A中的元素进行所有可能的四则混合运算所得到的值。

首先从集合A中任意取出两个数，如取出1和2，A＝A－{1，2}，对取出来的数分别进行不同的四则运算，1＋2＝3，1－2＝-1，1/2＝0.5，1×2＝2，将所得的结果再分别加入集合A，可得到B＝{3，3，4}，C＝{-1，3，4}，D＝{0.5，3，4}，E＝{2，3，4}四个新的集合，那么f（A）＝f（B）＋f（C）＋f（D）＋f（E），通过以上的计算就达到了分而治之的目的，问题规模就从4个数降到了3个数，成了3个数的4个子问题之和。

综上所述，可以得到递归解法为：

首先将给定的4个数放入数组Array中，将其作为参数传入函数f中，伪代码如下：

代码清单1-24

具体代码如下：

代码清单1-25

这种解法的思路比较清晰，但仍然是一种穷举算法，存在不少冗余计算，比如没有考虑到加法和乘法的交换率等，而且复杂度也没有降低。

可以对算法一的穷举算法进行简单的改进，如在满足交换律的加法和乘法运算中，我们规定，第一操作数必须小于第二操作数，就是说，如果A＞B，那么只进行B＋A的计算，若遇到A＋B的计算时则简单地返回。其实这是一种简单的剪枝策略，通过将某些冗余（或者达不到最优解）的穷举路径剪掉，达到一个较好的运算策略。

【解法二】

解法一中存在着大量的冗余计算，是否能够将这些冗余计算降低到最低呢？在解法二中我们将从另一个角度来思考该题。

仍然定义要计算的初始数据（题目中4张牌的数值）都放于集合A中（集合A为多重集合，因为允许出的牌中有重复面值），定义函数f（A）为对集合A中的元素进行所有可能的四则混合运算所得到的值。可以采用分治的思想，先将A划分为两个子集A₁和A－A₁，其中A₁为A的非空真子集（若A₁为空集或全集，则转换成了原问题），分别计算A₁和A－A₁中的元素进行四则混合运算所能得到的结果集合，即f（A₁）和f（A－A₁），然后对f（A₁）和f（A－A₁）这两个集合中的元素进行加减乘除运算，最后得到的所有集合的并集就是f（A）。

给定两个多重集合A和B（同上，因为允许出的牌中有重复的面值），定义两个集合中的元素运算如下：

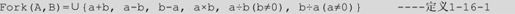
其中（a，b）∈A×B，“×”为集合的叉乘，即a∈A，b∈B，（a，b）为集合A和B中可能的两两组合，假设集合A₁中有n个元素，集合A₂中有m个元素，那么将有n×m个（a，b），而每对值需要分别进行6个计算（见Fork定义），既Fork（A₁，A₂）的结果集中将有6×n×m个元素。∪为集合的并运算。

Fork（A，B）实际上定义了两个集合中的元素两两进行加减乘除运算所能得到的全部结果集合，所以在计算Fork（A，B）的过程中，可以将重复出现的结果去掉，也就是说Fork（A，B）返回的结果集不再是多重集，而只是一个简单的集合了。通过去除重复出现的中间结果，也就是通过剪枝，可以在一定程度上提高效率。注意，这与Fork（A，B）允许A和B为多重集并不矛盾。

那么对于有理数组成的多重集合A（中间结果可能不再是整数），如果A至少有两个元素，则f（A）＝∪Fork（f（A₁），f（A－A₁）），其中A₁取遍A的所有非空真子集（若A₁为空集或全集，则转换成了原问题）。假设集合A中有n个元素，那么集合A的所有非空真子集个数为2n－2（减掉空集和全集），即f（A）的第一层递推式中共有（2n－2）/2个Fork函数（将所有的真子集按照原集合的划分两两配对）。

通过以上的分析，得到了另一种计算f（A）的方法。根据f（A）的定义式，可以简单地直接递归计算f（A），但那样会有很多冗余计算。

例如对于A＝{1，2，3，4}，如图1-26所示：

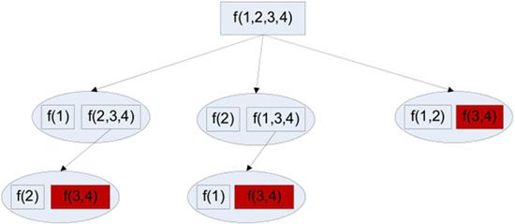
图1-26　对F函数分解示意图

图1-26是个树状结构（图中并未详细列出所有的情况），树的每个节点是一个集合，每个节点都为其子节点的并集。其中，椭圆形的节点代表其中的两个集合需要进行Fork()计算。

计算到最后，根节点中将保存f（A）＝f（{1，2，3，4}）的结果。

其中的计算冗余可举例如下：

计算f（A）的时候需要计算f（{2，3，4}）、f（1，3，4）和f（{3，4}），又因为

在计算f（{2，3，4}）和f（{1，3，4}）的时候又要重复地计算f（{3，4}），这就产生了冗余的计算，如图1-26中加了阴影的部分所示。针对冗余计算的部分，可以将已求解过的子问题（如上面的f（{3，4}））记录在一张表中，当再次需要求解该子问题时，即可直接从表中查询出该子问题的解。这种解决冗余的算法设计策略，其实包含了动态规划的思想。

解法二从集合划分和合并（Fork运算）的角度，对24点游戏进行解答。

在实际实现的时候，我们可以用二进制数来表示集合和子集的概念，由于24点游戏的输入集合A中只有四个元素（设A={a₀，a₁，a₂，a₃}），可以采用4位的二进制数来表示集合A及其真子集，当且仅当a_i（0＜＝i＜＝3）在某一个真子集中时，该真子集所代表的二进制数对应的第i位（从左到右）才为1，否则为0。如A₁＝{a₁，a₂，a₃}，则1110代表A₁，若A₂＝{a₀，a₃}，则0101代表A₂。故A的所有真子集的范围从1到2n－2（n＝4），即1到14。再用一个大小为2n－1（n＝4）数组S来保存f（i）（1＜＝i＜＝15），数组S的每一个元素S[i]都是一个集合（f（i）），其中S[2n－1]即为集合A中的所有元素通过四元运算和加括号所能得到的全部结果，通过检查S[2n－1]，即可得知某个输入是否有解。伪代码如下：

代码清单1-26

代码清单1-27

总结

解法一和解法二分别从不同的角度对24点游戏进行了解答，它们都很容易扩展到n张牌之和为m的游戏。若需要实现一个完整的游戏时，可预先将所有可能的输入都进行求解，并将输入和解按照某种数据结构进行组织（如hash等），这样在初始化结束之后，便可在O（1）的时间内对所有的输入返回其答案。

扩展问题

1．试试下面几个测试用例，看看你写的解法能不能算出正确的表达式来：

5，5，5，1

3，3，7，7

3，3，8，8

4，4，10，10

1，4，5，6

3，8，8，10

4，4，10，10

9，9，6，2

2．大家不妨考虑一下，如果要优化上述算法，可以从哪几个方面入手？

3．若给n张牌，要求最后结果为m，又该如何解呢？（提示，其实本题中的两种解法已经都能够求解该问题了。）

4．如果我们把阶乘（！）作为一个合法的运算符（当然只对正整数适用），上面的程序要怎么改进？（提示：在本题的两种解法的基础上，很容易能够运算扩展到阶乘（！）（只针对正整数），但要注意阶乘（！）只是一元运算符。）

附：扩展问题1的解答：

5×（5－1/5）＝24

7×（3＋3/7）＝24

8/（3－8/3）＝24

4/（1－5/6）＝24

（8×10－8）/3＝24

（10×10－4）/4＝24

9×（2＋6/9）＝24